Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 36) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 36)
Câu 1: Giải phương trình 4sin2x + 4sinx – 3 = 0.
Lời giải:
4sin2x + 4sinx – 3 = 0
⇔ 4sin2x – 2sinx + 6sinx – 3 =
⇔ 2sinx.(2sinx – 1) + 3(2sinx – 1) = 0
⇔ (2sinx – 1)(2sinx + 3) = 0
Vậy phương trình đã cho có nghiệm là .
Câu 2: Cho (d): y = mx – 2 và (P): y = –x2.
a) Chứng minh rằng (d) luôn cắt (P) tại hai điểm nằm về hai phía của trục tung với mọi giá trị của m.
b) Tìm m sao cho y1 + y2 = –8.y1.y2.
Lời giải:
a) Phương trình hoành độ giao điểm của (d) và (P): mx – 2 = –x2.
⇔ x2 + mx – 2 = 0 (1)
Theo Viet: .
.
Suy ra phương trình (1) luôn có 2 nghiệm trái dấu.
Vậy (d) luôn cắt (P) tại hai điểm nằm về hai phía của trục tung với mọi giá trị của m.
b) Ta có y1 = mx1 – 2; y2 = mx2 – 2.
Theo đề, ta có y1 + y2 = –8.y1.y2.
⇔ mx1 – 2 + mx2 – 2 = –8(mx1 – 2)(mx2 – 2).
⇔ m(x1 + x2) – 4 = –8(m2x1x2 – 2mx1 – 2mx2 + 4).
⇔ m.(–m) – 4 = –8[m2.(–2) – 2m(x1 + x2) + 4].
⇔ –m2 – 4 = –8[–2m2 – 2m.(–m) + 4].
⇔ –m2 – 4 = –8(–2m2 + 2m2 + 4).
⇔ –m2 – 4 = –32.
⇔ m2 – 28 = 0.
.
Vậy thỏa mãn yêu cầu bài toán.
Lời giải:
Phương trình hoành độ giao điểm của (d) và (P): 2x + m = x2.
⇔ x2 – 2x – m = 0 (1)
Theo Viet: .
Ta có (d) cắt (P) tại hai điểm nằm về hai phía của trục tung.
⇔ Phương trình (1) có 2 nghiệm trái dấu.
⇔ P < 0.
⇔ –m < 0.
⇔ m > 0.
Vậy m > 0 thỏa mãn yêu cầu bài toán.
Câu 4: Từ 15 học sinh ưu tú của một lớp có bao nhiêu cách:
a) Chọn 7 học sinh làm cán bộ lớp.
b) Chọn 7 học sinh làm cán bộ lớp trong đó có: 1 lớp trưởng, 2 lớp phó, 4 tổ trưởng.
Lời giải:
a) Chọn 7 học sinh làm cán bộ lớp từ 15 học sinh ưu tú của lớp đó có: cách chọn.
b) Chọn 1 lớp trưởng từ 15 học sinh ưu tú có: 15 cách chọn.
Chọn 2 lớp phó từ 14 học sinh ưu tú còn lại có: cách chọn.
Chọn 4 tổ trưởng từ 12 học sinh ưu tú còn lại có: cách chọn.
Vậy chọn 7 học sinh làm cán bộ lớp trong đó có 1 lớp trưởng, 2 lớp phó, 4 tổ trưởng thì có cách chọn.
Câu 5: Tính B = x5 – 15x4 + 16x3 – 29x2 + 13x tại x = 14.
Lời giải:
Với x = 14, ta có:
⦁ x + 1 = 15;
⦁ x + 2 = 16;
⦁ 2x + 1 = 29;
⦁ x – 1 = 13.
Ta có B = x5 – 15x4 + 16x3 – 29x2 + 13x
= x5 – (x + 1)x4 + (x + 2)x3 – (2x + 1)x2 + (x – 1)x
= x5 – x5 – x4 + x4 + 2x3 – 2x3 – x2 + x2 – x
= –x = –14.
Vậy B = –14 khi x = 14.
Lời giải:
Phương trình hoành độ giao điểm (P) và (d): x2 = 2x – m.
⇔ x2 – 2x + m = 0 (1)
Ta có ∆’ = (–1)2 – 1.m = 1 – m.
Theo đề, ta có (P) và (d) có điểm chung duy nhất.
⇔ Phương trình (1) có nghiệm duy nhất.
⇔ ∆’ = 0.
⇔ 1 – m = 0.
⇔ m = 1.
Vậy m = 1 thỏa mãn yêu cầu bài toán.
Câu 7: Tìm giá trị nhỏ nhất của A = 2x2 – 8x + 1.
Lời giải:
A = 2x2 – 8x + 1 = 2(x2 – 4x + 4) – 7 = 2(x – 2)2 – 7.
Ta có (x – 2)2 ≥ 0, ∀x ∈ ℝ.
⇔ 2(x – 2)2 ≥ 0, ∀x ∈ ℝ.
⇔ 2(x – 2)2 – 7 ≥ –7, ∀x ∈ ℝ.
⇔ A ≥ –7, ∀x ∈ ℝ.
Dấu “=” xảy ra ⇔ x – 2 = 0 ⇔ x = 2.
Vậy giá trị nhỏ nhất của A bằng –7 khi và chỉ khi x = 2.
Câu 8: Tìm giá trị nhỏ nhất của A(x) = x2 – 4x + 24.
Lời giải:
A(x) = x2 – 4x + 24 = x2 – 4x + 4 + 20 = (x – 2)2 + 20.
Ta có (x – 2)2 ≥ 0, ∀x ∈ ℝ.
⇔ (x – 2)2 + 20 ≥ 20, ∀x ∈ ℝ.
⇔ A ≥ 20, ∀x ∈ ℝ.
Dấu “=” xảy ra ⇔ x – 2 = 0 ⇔ x = 2.
Vậy giá trị nhỏ nhất của A bằng 20 khi và chỉ khi x = 2.
Lời giải:
Chiều rộng của mảnh đất đó là: (m)
Diện tích của mảnh đất đó là: 36.9 = 324 (m2).
Đáp số: 324 m2.
Câu 10: Cho A = (–∞; –2], B = [3; +∞) và C = (0; 4). Khi đó, (A ∪ B) ∩ C là:
A. [3; 4];
B. (–∞; –2] ∪ (3; +∞);
C. [3; 4);
D. (–∞; –2) ∪ [3; +∞).
Lời giải:
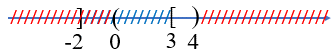
Ta có A ∪ B = (–∞; –2] ∪ [3; +∞).
Suy ra (A ∪ B) ∩ C = [3; 4).
Vậy ta chọn phương án C.
Câu 11: Có bao nhiêu số tự nhiên có 3 chữ số được lập từ sáu chữ số 1; 2; 3; 4; 5; 6?
A. 120;
B. 216;
C. 256;
D. 20.
Lời giải:
Gọi là số tự nhiên có 3 chữ số.
Ta có:
⦁ a có 6 cách chọn;
⦁ b có 6 cách chọn;
⦁ c có 6 cách chọn.
Áp dụng quy tắc nhân, ta có 6.6.6 = 216 số tự nhiên có 3 chữ số được tạo thành từ sáu chữ số đã cho.
Vậy ta chọn phương án B.
Câu 12: Hình lăng trụ có đáy là thập giác lồi có bao nhiêu cạnh?
Lời giải:
Hình lăng trụ có đáy là thập giác lồi có tất cả 2.10 = 20 cạnh đáy.
Khi đó hình lăng trụ này có tất cả 10 mặt bên nên có 9 đường cao.
Vậy hình lăng trụ có đáy là thập giác lồi có 29 cạnh.
Câu 13: Tìm m để đường thẳng y = 2x – 1 và y = 3x + m cắt nhau tại một điểm nằm trên trục hoành.
Lời giải:
Gọi (d): y = 2x – 1 và (d’): y = 3x + m.
Trục Ox: y = 0.
Phương trình hoành độ giao điểm của (d) và Ox: .
Với , ta có: y = 0.
Suy ra giao điểm của (d) và trục hoành là .
Yêu cầu bài toán ⇔ Đường thẳng (d’) đi qua điểm .
Ta có I ∈ (d’). Suy ra .
.
Vậy thỏa mãn yêu cầu bài toán.
Lời giải:
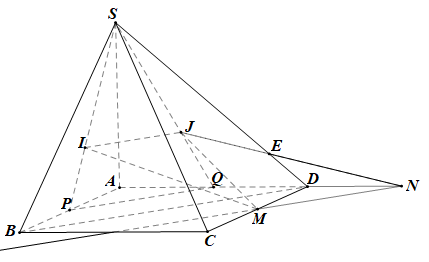
Gọi P, Q lần lượt là trung điểm của AB, AD.
Khi đó PQ là đường trung bình của tam giác ABD nên PQ // BD.
Do I, J lần lượt là trọng tâm tam giác SAB, SAD nên .
Do đó IJ // PQ, suy ra IJ // BD
Có IJ // BD, IJ ⊂ (IJM), BD ⊂ (ABCD)
⇔ giao tuyến của (IJM) và (ABCD) là đường thẳng qua M và song song với BD.
Đường thẳng này cắt AD tại N.
Khi đó mp(IJM) chính là mp (IJNM), mp(SAD) chính là mp(SAN)
Trong mp(SAN), JN cắt SD tại E.
Ta có: JN ∩ SD = {E}; JN ⊂ (IJM)
Khi đó E là giao điểm của SD và (IJM).
Lời giải:
Khi dịch dấu phẩy của số bé sang trái một hàng, ta thấy số bé ban đầu gấp 10 lần số bé sau khi dịch dấu phẩy.
HIệu số bé ban đầu và số bé sau khi dịch dấu phẩy là: 117,83 – 66,8 = 51,03.
Số bé ban đầu là: 51,03 : (10 – 1) ⨯ 10 = 56,7.
Số lớn là: 56,7 + 66,8 = 123,5.
Đáp số : 123,5.
Lời giải:
– Lấy nước đổ vào đầy cái cốc loại 250 ml, sau đó đổ hết vào cái cốc loại 400 ml.
– Tiếp tục lấy nước đổ vào đầy cái cốc loại 250 ml, sau đó đổ vào cái cốc loại 400 ml cho đến khi cái cốc loại 400 ml chứa đầy nước.
– Khi đó trong cái cốc loại 250 ml còn lại 100 ml nước.
Câu 17: Cho 2 tập khác rỗng A = (m – 1; 4]; B = (–2; 2m + 2), m ∈ ℝ. Tìm m để A ⊂ B.
Lời giải:
Ta có
⇔ 1 < m < 5.
Vậy 1 < m < 5 thỏa mãn yêu cầu bài toán.
Câu 18: Tìm số tự nhiên a, b biết ƯCLN(a, b) = 4 và a + b = 48.
Lời giải:
Ta thấy a, b ∈ ℕ.
Ta có ƯCLN(a, b) = 4.
Suy ra a = 4m và b = 4n, với m, n ∈ ℕ* và (m, n) = 1.
Ta lại có a + b = 48.
Suy ra 4m + 4n = 48.
Do đó 4(m + n) = 48.
Vì vậy m + n = 48 : 4 = 12.
Suy ra m + n = 11 + 1 = 10 + 2 = 9 + 3 = 8 + 4 = 7 + 5 = 6 + 6.
Giả sử a ≥ b. Suy ra m ≥ n.
Mà (m, n) = 1.
Khi đó hoặc hoặc .
Với , ta có: (nhận)
Với , ta có: (nhận)
Với , ta có: (nhận)
Vậy hai số tự nhiên cần tìm là: 44 và 4; 28 và 20; 24 và 24.
Câu 20: Đơn giản biểu thức sau khi bỏ dấu ngoặc:
a) (a + b – c) – (b – c + d);
b) –(a – b + c) + (a – b + d);
c) (a + b) – (–a + b – c);
d) –(a + b) + (a + b + c);
e) (a – b + c) – (a – b + c);
f) –(a – b – c) + (a – b – c).
Lời giải:
a) (a + b – c) – (b – c + d)
= a + b – c – b + c – d
= a + (b – b) + (–c + c) – d
= a – d.
b) –(a – b + c) + (a – b + d)
= –a + b – c + a – b + d
= (a – a) + (b – b) – c + d
= d – c.
c) (a + b) – (–a + b – c)
= a + b + a – b + c
= (a + a) + (b – b) + c
= 2a + c.
d) –(a + b) + (a + b + c)
= –a – b + a + b + c
= (–a + a) + (–b + b) + c
= c.
e) (a – b + c) – (a – b + c)
= a – b + c – a + b – c
= (a – a) + (–b + b) + (c – c)
= 0.
f) –(a – b – c) + (a – b – c)
= –a + b + c + a – b – c
= (–a + a) + (b – b) + (c – c)
= 0.
Lời giải:
Số đối của 24 là –24.
Câu 22: Cho 3x2 + 3y2 = 10xy với y > x > 0. Tính giá trị của biểu thức .
Lời giải:
Ta có:
Suy ra K = 2 hoặc K = – 2.
Mà y > x > 0 nên x + y > 0 và x – y < 0, suy ra .
Do đó K = – 2.
Câu 23: Giải phương trình 5sin2x + 3sinxcosx – 4cos2x = 2.
Lời giải:
Ta xét phương trình: 5sin2x + 3sinxcosx – 4cos2x = 2 (1)
Với cosx = 0 ta có (1) trở thành:
5sin2x = 2 (vô lí vì khi cosx = 0 thì cos2x = 0 nên sin2x = 1)
Với cosx ≠ 0, ta chia 2 vế của (1) cho cos2x được:
⇔ 5tan2x + 3tanx – 4 = 2(tan2x + 1)
⇔ 3tan2x + 3tanx – 6 = 0
⇔ tan2x + tanx – 2 = 0
⇔ (tanx – 1)(tanx + 2) = 0
(thỏa mãn)
Vậy phương trình đã cho có nghiệm là .
A. A ∩ B = [–4; 2];
B. A ∩ B = (–4; 2);
C. A ∩ B = [–4; +∞);
D. A ∩ B = (–∞; 2).
Lời giải:
Đáp án đúng là: A
Vì A ∩ C là đoạn có độ dài bằng 7 nên a – (–5) = 7.
⇔ a = 2.
Khi đó A = (–∞; 2].
Vì B ∩ C là đoạn có độ dài bằng 9 nên 5 – b = 9.
⇔ b = –4.
Khi đó B = [–4; +∞).
Vậy A ∩ B = [–4; 2].
Do đó ta chọn phương án A.
Câu 25: Tìm số tự nhiên n để giá trị biểu thức sau là số nguyên tố: A = n3 – 4n2 + 4n – 1.
Lời giải:
Điều kiện: n ∈ ℕ.
Ta có A = n3 – 4n2 + 4n – 1
= (n3 – 1) – (4n2 – 4n)
= (n – 1)(n2 + n + 1) – 4n(n – 1)
= (n – 1)(n2 + n + 1 – 4n)
= (n – 1)(n2 – 3n + 1).
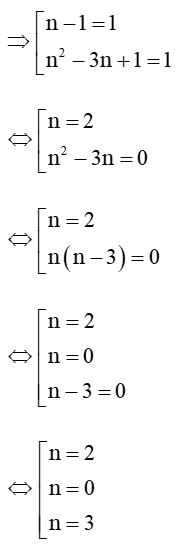
Để A là số nguyên tố thì A là tích của 1 và chính nó (A > 1).
Với n = 2, ta có: A = n3 – 4n2 + 4n – 1 = 23 – 4.22 + 4.2 – 1 = –1 < 1.
Do đó ta loại n = 2.
Với n = 0, ta có: A = n3 – 4n2 + 4n – 1 = 03 – 4.02 + 4.0 – 1 = –1 < 1.
Do đó ta loại n = 0.
Với n = 3, ta có: A = n3 – 4n2 + 4n – 1 = 33 – 4.32 + 4.3 – 1 = 2 > 1.
Do đó ta nhận n = 3.
So với điều kiện n ∈ ℕ, ta nhận n = 3.
Vậy n = 3 thỏa mãn yêu cầu bài toán.
Câu 26: Cho hai tập hợp X = (0; 3] và Y = (a; 4). Tìm tất cả các giá trị của a ≤ 4 để X ∩ Y ≠ ∅.
A. ;
B. a < 3;
C. a < 0;
D. a > 3.
Lời giải:
Đáp án đúng là: B
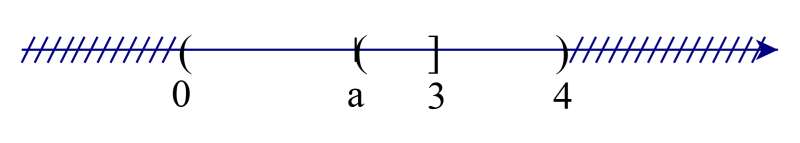
Để X ∩ Y ≠ ∅ thì a < 3.
So với điều kiện a ≤ 4, ta nhận a < 3.
Vậy a < 3 thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án B.
Câu 27: Tìm x biết: x4 + 2x3 – 6x – 9 = 0.
Lời giải:
Ta có x4 + 2x3 – 6x – 9 = 0.
⇔ (x4 + 2x3 + x2) – (x2 + 6x + 9) = 0.
⇔ (x2 + x)2 – (x + 3)2 = 0.
⇔ (x2 + x – x – 3)(x2 + x + x + 3) = 0.
⇔ (x2 – 3)(x2 + 2x + 3) = 0.
Vậy .
Câu 28: Giải phương trình cos2x – 3cosx + 2 = 0.
Lời giải:
Ta có cos2x – 3cosx + 2 = 0.
⇔ 2cos2x – 1 – 3cosx + 2 = 0.
⇔ 2cos2x – 3cosx + 1 = 0.
Vậy phương trình đã cho có nghiệm là .
Câu 29: Giải phương trình lượng giác: sin22x + sin24x = sin26x.
Lời giải:
Ta có sin22x + sin24x = sin26x.
⇔ 1 – cos4x + 1 – cos8x = 1 – cos12x
⇔ (cos12x – cos4x) + (1 – cos8x) = 0
⇔ –2sin8x.sin4x + 2sin24x = 0
⇔ –2sin4x.(sin8x – sin4x) = 0
Vậy phương trình đã cho có nghiệm là .
Câu 30: Giải phương trình sau: .
Lời giải:
Ta có .
⇔ 1 – cos4x = 1
⇔ cos4x = 0
Vậy phương trình đã cho có nghiệm là .
Lời giải:
Gọi số cần tìm là , với 1 ≤ a1 ≤ 5 và a6 lẻ.
Đặt X = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}.
Trường hợp 1: a1 lẻ.
Do a1 ∈ {1; 3; 5} nên a1 có 3 cách chọn.
Do a6 ∈ {1; 3; 5; 7; 9} và bỏ đi {a1} nên a6 có 4 cách chọn.
Do a2 ∈ X và bỏ đi {a1, a6} nên a2 có 8 cách chọn.
Do a3 ∈ X và bỏ đi {a1, a6, a2} nên a3 có 7 cách chọn.
Do a4 ∈ X và bỏ đi {a1, a6, a2, a3} nên a4 có 6 cách chọn.
Do a5 ∈ X và bỏ đi {a1, a6, a2, a3, a4} nên a5 có 5 cách chọn.
Áp dụng quy tắc nhân, ta có 3.4.8.7.6.5 = 20160 số tự nhiên thỏa mãn trường hợp 1.
Trường hợp 2: a1 chẵn.
Do a1 ∈ {2; 4} nên a1 có 2 cách chọn.
Do a6 ∈ {1; 3; 5; 7; 9} nên a6 có 5 cách chọn.
Do a2 ∈ X và bỏ đi {a1, a6} nên a2 có 8 cách chọn.
Do a3 ∈ X và bỏ đi {a1, a6, a2} nên a3 có 7 cách chọn.
Do a4 ∈ X và bỏ đi {a1, a6, a2, a3} nên a4 có 6 cách chọn.
Do a5 ∈ X và bỏ đi {a1, a6, a2, a3, a4} nên a5 có 5 cách chọn.
Áp dụng quy tắc nhân, ta có 2.5.8.7.6.5 = 16800 số tự nhiên thỏa mãn trường hợp 2.
Vậy theo quy tắc cộng, ta có tất cả 20160 + 16800 = 36960 số tự nhiên thỏa mãn yêu cầu bài toán.
Lời giải:
Số lẻ nhỏ nhất có ba chữ số khác nhau là số 103.
Số chẵn lớn nhất gồm 2 chữ số chẵn khác nhau là số 88.
Vậy tổng của hai số trên là: 103 + 88 = 191.
Câu 33: Tính tổng sau: 1 + 2 + 3 + … + 99.
Lời giải:
Ta đặt A = 1 + 2 + 3 + … + 99.
Số các số hạng của A là: (99 – 1) : 1 + 1 = 99.
Khi đó A = (99 + 1) . 99 : 2 = 4950.
Vậy A = 4950.
Câu 34: Giải phương trình: x3(x2 – 7)2 – 36x = 0.
Lời giải:
Ta có x3(x2 – 7)2 – 36x = 0.
⇔ x.[x2(x2 – 7)2 – 36] = 0.
⇔ x.[x.(x2 – 7) – 6].[x.(x2 – 7) + 6] = 0.
⇔ x.(x3 – 7x – 6)(x3 – 7x + 6) = 0.
⇔ x.[x2(x + 1) – x.(x + 1) – 6(x + 1)].[x2.(x – 1) + x.(x – 1) – 6(x – 1)] = 0.
⇔ x.(x + 1)(x2 – x – 6)(x – 1)(x2 + x – 6) = 0.
⇔ x.(x + 1)(x – 1)[x.(x – 3) + 2(x – 3)].[x.(x + 3) – 2(x + 3)] = 0.
⇔ x.(x + 1)(x – 1)(x – 3)(x + 2)(x + 3)(x – 2) = 0.
Vậy tập nghiệm của phương trình đã cho là: S = {0; –1; 1; 3; –2; –3; 2}.
Câu 35: Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:
a) A = cos4x – cos2x + sin2x;
b) B = sin4x – sin2x + cos2x.
Lời giải:
a) A = cos4x – cos2x + sin2x
= cos4x – cos2x + 1 – cos2x
= cos4x – 2cos2x + 1
= (cos2x – 1)2
= (–sin2x)2
= sin4x.
Ta có –1 ≤ sinx ≤ 1, ∀x.
⇔ 0 ≤ sin4x ≤ 1, ∀x.
⇔ 0 ≤ A ≤ 1, ∀x.
Dấu “=” xảy ra
Vậy maxA = 1 khi và chỉ khi và minA = 0 khi và chỉ khi x = kπ (k ∈ ℤ).
b) B = sin4x – sin2x + cos2x
= sin4x – sin2x + 1 – sin2x
= sin4x – 2sin2x + 1
= (sin2x – 1)2
= (–cos2x)2
= cos4x.
Ta có –1 ≤ cosx ≤ 1, ∀x.
⇔ 0 ≤ cos4x ≤ 1, ∀x.
⇔ 0 ≤ B ≤ 1, ∀x.
Dấu “=” xảy ra
Vậy maxB = 1 khi và chỉ khi x = kπ và minB = 0 khi và chỉ khi (k ∈ ℤ).
Câu 36: Cho các đa thức sau: A = x3 + 4x2 + 3x – 7 và B = x + 4.
a) Tính A : B.
b) Tìm x ∈ ℤ sao cho A chia hết cho B.
Lời giải:
a)
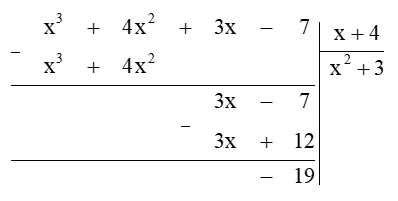
b) A : B = (x + 4)(x2 + 3) – 19.
Ta có A ⋮ B ⇔ 19 ⋮ (x + 4).
Ư(19) ∈ {–19; –1; 1; 19}.
Ta có bảng sau:
| x | –19 | –1 | 1 | 19 |
| x + 4 | –23 | –5 | –3 | 15 |
Vì x ∈ ℤ nên x ∈ {–23; –5; –3; 15}.
Vậy x ∈ {–23; –5; –3; 15} thì A chia hết cho B.
Lời giải:
Gọi số nhân với 39 là a, ta có tích riêng thứ nhất là 9a, tích riêng thứ hai là 3a.
Vì đặt nhân nhầm các tích riêng thẳng cột nên tích sai là 9a + 3a = 259,2.
Hay 12a = 259,2 ⇒ a = 259,2 : 12 = 21,6.
Vậy tích đúng của phép nhân đó là: 21,6.39 = 842,4.
Lời giải:
1 chiếc áo hết số vải là: 19,5 : 13 = 1,5 (m)
1 cái quần hết số vải là: 12,6 : 12 = 1,05 (m)
May 1 bộ quần áo hết số m vải là: 1,5 + 1,05 = 2,55 (m).
Lời giải:
1 km ô tô đó tiêu thụ hết số lít xăng là: 12,5 : 100 = 0,125 (lít).
60 km ô tô tiêu thụ hết số lít xăng là: 60 × 0,125 = 7,5 (lít).
Lời giải:
Gọi số bị chia cũ là a; số chia cũ là b.
Do đó, số chia mới là: 18b
Gọi thương mới là n.
Theo đề bài, ta có: a : b = 468.
Giả sử a : 18b = n
a : 18 : b = n
(a : b) : 18 = n
Nên 468 : 18 = n ⇒ n = 26.
Vậy nếu giữ nguyên số bị chia và số chia gấp 18 lần thì thương mới là 26.
Câu 41: Tổng của tất cả các số nguyên a mà –7 < a ≤ 7 bằng bao nhiêu?
Lời giải:
Các số a thỏa mãn – 7 < a ≤ 7 là – 6; – 5; – 4; – 3; – 2; – 1; 0; 1; 2; 3; 4; 5; 6; 7.
Tổng là: (–6) + (–5) + (–4) + ... + 7 = 7.
Lời giải:
Trung bình mỗi giờ xe máy đi: 121 : 4 = 30,25 (km)
Trung bình mỗi giờ ô tô đi: 111 : 2 = 55,5 (km)
Trung bình mỗi giờ ô tô đi hơn xe máy: 55,5 – 30,25 = 25,25 (km).
Lời giải:
Hiệu số phần bằng nhau là: 5 – 1 = 4 (phần).
4 lần số hạng thứ nhất là: 329,3 – 102,1 = 227,2.
Số thứ nhất là: 227,2 : 4 = 56,8.
Số thứ hai là: 102,1 – 56,8 = 45,3.
Câu 44: Tìm x, biết: 35,8 + x × 4 = 100.
Lời giải:
35,8 + x × 4 = 100
x × 4 = 100 – 35,8
x × 4 = 64,2
x = 64,2 : 4
x = 16,05.
Câu 45: Tìm x: (x – 12) – 15 = 20 – (17 + x).
Lời giải:
Ta có: x – 12 – 15 = 20 – 17 – x
2x = 30
x = 15
Vậy x = 15.
Câu 46: Tìm x thuộc Ư(20)và x > 8.
Lời giải:
Tập hợp các ước của 20, ta có: Ư(20) = {1; 2; 4; 5; 10; 20}.
Vì x > 8 nên suy ra có 2 ước thỏa mãn yêu cầu là: 10 và 20.
Câu 47: Tìm x, biết: 5.(12 – x) – 20 = 30.
Lời giải:
5.(12 – x) – 20 = 30
5.(12 – x) = 50
12 – x = 50 : 5
12 – x = 10
x = 12 – 10
x = 2
Vậy x = 2.
a. Tính thể tích của hồ bơi.
b. Tính diện tích cần lát gạch bên trong lòng hồ (mặt đáy và 4 mặt xung quanh).
c. Biết gạch hình vuông dùng để lát hồ bơi có cạnh 50cm. Hỏi cần mua ít nhất bao nhiêu viên gạch để lát bên trong hồ bơi.
Lời giải:
a. Thể tích hồ bơi là: V = 12.5.3 = 180 (m3).
b. Diện tích cần lát gạch xung quanh là:
c. Đổi 50cm = 0,5m
Diện tích 1 viên gạch là: 0,5.0,5 = 0,25 (m2).
Cần mua ít nhất số viên gạch để lát bên trong hồ bơi là: 162 : 0,25 = 648 (viên).
Câu 49: Trong phép tính 121,23 : 14 và có thương là 8,65, vậy số dư là bao nhiêu?
A. 13.
B. 1,3.
C. 0,13.
D. 0,013.
Lời giải:
Đáp án đúng là: C
Số dư là: 121,23 – 8,65 × 14 = 0,13.
Đáp số: 0,13.
Câu 50: Giá trị biểu thức 15,5 + 6,25 : 25 là
A. 0,87.
B. 15,75.
C. 18.
D. 157,5.
Lời giải:
Đáp án đúng là: B
Ta có: 6,25 : 25 = 0,25.
Do đó 15,5 + 6,25 : 25 = 15,5 + 0,25 = 15,75.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.