Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 36) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho hình chóp S.ABCD có đáy là hình bình hành
Câu 14: Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm I, J lần lượt là trọng tâm tam giác SAB, SAD. Gọi M là trung điểm của CD. Tìm giao điểm E của SD và mặt phẳng IJM.
Lời giải:
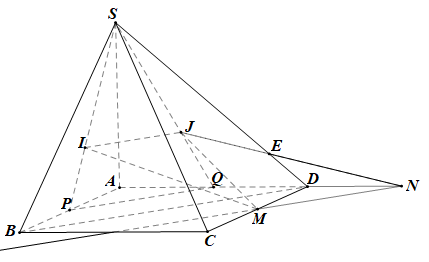
Gọi P, Q lần lượt là trung điểm của AB, AD.
Khi đó PQ là đường trung bình của tam giác ABD nên PQ // BD.
Do I, J lần lượt là trọng tâm tam giác SAB, SAD nên .
Do đó IJ // PQ, suy ra IJ // BD
Có IJ // BD, IJ ⊂ (IJM), BD ⊂ (ABCD)
⇔ giao tuyến của (IJM) và (ABCD) là đường thẳng qua M và song song với BD.
Đường thẳng này cắt AD tại N.
Khi đó mp(IJM) chính là mp (IJNM), mp(SAD) chính là mp(SAN)
Trong mp(SAN), JN cắt SD tại E.
Ta có: JN ∩ SD = {E}; JN ⊂ (IJM)
Khi đó E là giao điểm của SD và (IJM).
Xem thêm các bài giải Tổng hợp kiến thức môn Toán hay, chi tiết khác:
Câu 1: Giải phương trình 4sin2x + 4sinx – 3 = 0.
Câu 2: Cho (d): y = mx – 2 và (P): y = –x2.
Câu 4: Từ 15 học sinh ưu tú của một lớp có bao nhiêu cách:
Câu 5: Tính B = x5 – 15x4 + 16x3 – 29x2 + 13x tại x = 14.
Câu 7: Tìm giá trị nhỏ nhất của A = 2x2 – 8x + 1.
Câu 8: Tìm giá trị nhỏ nhất của A(x) = x2 – 4x + 24.
Câu 10: Cho A = (–∞; –2], B = [3; +∞) và C = (0; 4). Khi đó, (A ∪ B) ∩ C là:
Câu 11: Có bao nhiêu số tự nhiên có 3 chữ số được lập từ sáu chữ số 1; 2; 3; 4; 5; 6?
Câu 12: Hình lăng trụ có đáy là thập giác lồi có bao nhiêu cạnh?
Câu 13: Tìm m để đường thẳng y = 2x – 1 và y = 3x + m cắt nhau tại một điểm nằm trên trục hoành.
Bài viết cùng bài học:




