Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 25) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 25)
Lời giải:
Gọi số học sinh dự thi của trường A và B lần lượt là x và y (x, y ∈ N*; x, y < 450)
Ta có x + y = 450 (1)
Vì tổng số học sinh trúng tuyển của cả hai trường bằng 45 số học sinh dự thi của hai trường nên ta có 34x+910y=45(x+y)=45.450=360 (2)
Từ (1) và (2) ta có hệ phương trình
{x+y=45034x+910y=360⇔{x=450−y15x+18y=7200⇔{x=450−y15(450−y)+18y=7200
⇔{x=450−y6750−15y+18y=7200⇔{x=450−y3y=450⇔{x=300y=150 (thỏa mãn)
Vậy trường A có 300 học sinh dự thi, trường B có 150 học sinh dự thi.
Lời giải:
Gọi số học sinh dự thi của trường A và B lần lượt là x và y (x, y ∈ N*; x, y < 750)
Ta có x + y = 750 (1)
Số học sinh trúng tuyển của trường A là 0,8x (học sinh)
Số học sinh trúng tuyển của trường B là 0,7y (học sinh)
Vì số học sinh trúng tuyển của cả hai trường là 560 học sinh nên ta có phương trình
0,8x + 0,7y = 560 (2)
Từ (1) và (2) ta có hệ phương trình
{x+y=7500,8x+0,7y=560⇔{x=750−y0,8(750−y)+0,7y=560
⇔{x=750−y600−0,8y+0,7y=560⇔{x=750−yy=400⇔{x=350y=400 (thỏa mãn)
Vậy trường A có 350 học sinh dự thi, trường B có 400 học sinh dự thi.
Lời giải:
Số nghịch đảo của 30 là 130
Số nghịch đảo của 42 là 142
Số nghịch đảo của 56 là 156
Số nghịch đảo của 72 là 172
Số nghịch đảo của 90 là 190
Tổng các số nghịch đảo là:

Vậy tổng của các số nghịch đảo bằng 110 .
Câu 4: Cho 4 điểm A, B, C, D bất kì. Chứng minh →AB+→CD=→AD+→CB
Lời giải:
Ta có →AB+→CD=(→AD+→DB)+(→CB+→BD)
→AD+→CB+→BD+→DB=→AD+→CB+→0=→AD+→CB
Vậy →AB+→CD=→AD+→CB .
Hãy viết giả thiết và kết luận của định lí
Lời giải:
|
GT |
^xOy=m° ^xOy,^x'Oy kề bù Ot là phân giác của ^xOy Ot’ là phân giác của ^x'Oy |
|
KL |
^tOt'=90°
|
Câu 6: Cho hình chóp S.ABCD có M nằm trên SC.
a) Tìm giao điểm của AM và mặt phẳng (SBD).
b) N nằm trên BC. Tìm giao điểm của SD với mặt phẳng (AMN).
Lời giải:
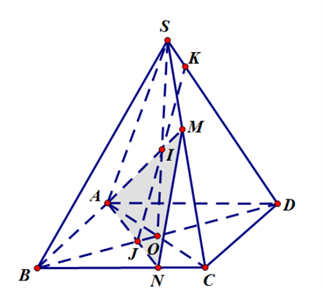
a) Gọi O là giao điểm của AC và BD
Trong (SAC) gọi SO cắt AM tại I
Ta có SO ⊂ (SBD) nên giao điểm của AM và mp (SBD) là I
b) Gọi giao điểm của AN và BD là J
Trong (SBD) gọi giao của IJ và SD là K
Ta có JI ⊂ (AMN) nên giao điểm của SD và (AMN) là K
Vậy giao điểm của SD và (AMN) là K.
A. MN // mp(ABCD);
B. MN // mp(SAB);
C. MN // mp(SCD);
D. MN // mp(SBC).
Lời giải:
Đáp án đúng là A
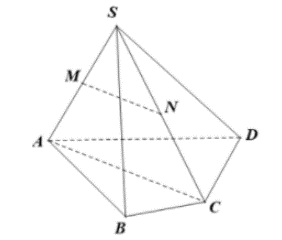
Xét tam giác SAC có
M là trung điểm của SA
N là trung điểm của SC
Suy ra MN là đường trung bình
Do đó MN // SA
Ta có :
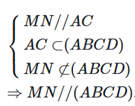
Vậy ta chọn đáp án A.
Lời giải:
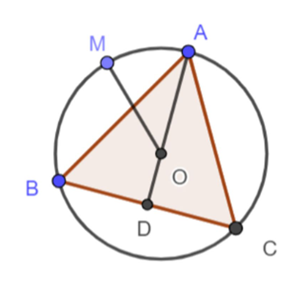
Tam giác ABC nội tiếp (O) và tam giác ABC đều nên O là trọng tâm tam giác ABC
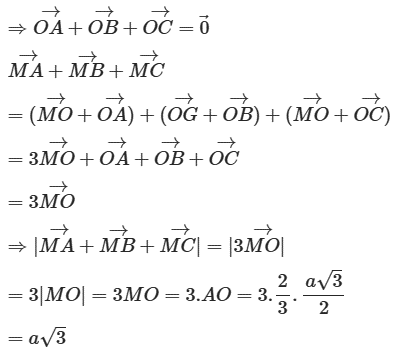
Vậy |→MA+→MB+→MC|=a√3.
Lời giải:
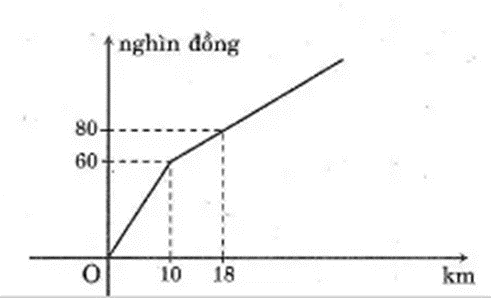
a) Số tiền phải trả cho 10 km đầu tiên là:
10 500 x 10 = 105 000 (đồng)
Số tiền phải trả cho 11 km tiếp theo là:
9 200 x 11 = 101 200 (đồng)
Tổng số tiền khách phải trả khi đi quãng đường 21 km là:
105 000 + 101 200 = 206 200 (đồng)
Vậy số tiền khách phải trả khi đi quãng đường 21 km là 206 200 đồng.
b) Nếu x < 10 thì p(x) = 10 500 . x
Nếu x > 10 thì P(x) = 10 500 x 10 + 9 200 . x = 105 000 + 9 200 . x
Lời giải:
Khi 0 ≤ x ≤ 10, tức là quãng đường đi nằm trong 10 km đầu tiên
Số tiền phải trả là f(x) = 6x (nghìn đồng)
Khi x > 10, tức quãng đường đi trên 10 km
Số tiền phải trả là f(x) = 60 + 2,5(x – 10) = 2,5x + 35
Ta có f(10) = 6 . 10 = 60
f(18) = 2,5 . 18 + 35 = 80
Bảng biến thiên
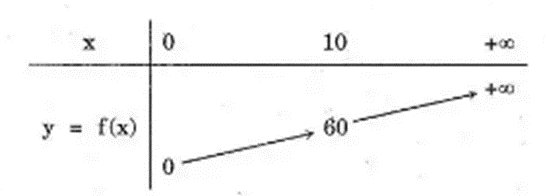
Đồ thị y = f(x)
Lời giải:
Ta đặt số có 6 chữ số đó là: abcdef
Số đúng là: 6bcde1
Số học sinh viết nhầm là: 1bcde6
Số đó giảm đi số đơn vị là:
6bcde1 - 1bcde6 = 60 000 – 10 000 + 6 – 1 = 50 005 (đơn vị)
Vậy số đó giảm đi 50 005 đơn vị.
Lời giải:
Ta đặt số có 6 chữ số đó là: abcdef
Số đúng là: 6bcde5
Số học sinh viết nhầm là: 5bcde6
Số đó giảm đi số đơn vị là:
6bcde5 - 5bcde6 = 60 000 – 50 000 + 6 – 5 = 10 001 (đơn vị)
Vậy số đó giảm đi 10 001 đơn vị.
Câu 13: Rút gọn biểu thức: x−y+3√x+3√y√x−√y+3 .
Lời giải:
Điều kiện xác định: x ≥ 0, y ≥ 0, √x−√y≠−3
Ta có:
x−y+3√x+3√y√x−√y+3=(√x−√y).(√x+√y)+3(√x+√y)√x−√y+3=(√x+√y).(√x−√y+3)√x−√y+3=√x+√y
Vậy giá trị biểu thức rút gọn bằng √x+√y
Câu 14: Tìm các số không âm x,y sao cho biểu thức A đạt giá trị nhỏ nhất
Lời giải:
Điều kiện xác định: x ≥ 3, y ≥ 2021
Ta có:
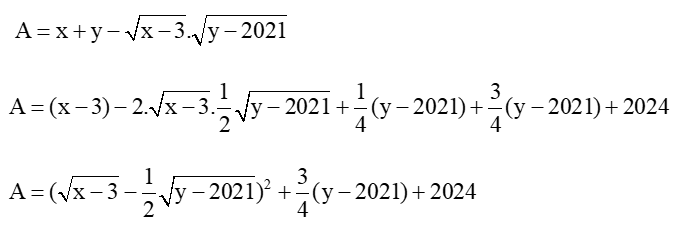
Vì (√x−3−12√y−2021)2≥0 , 34(y−2021)≥0
Nên (√x−3−12√y−2021)2+34(y−2021)+2024≥2024
Hay A ≥ 2024
Dấu “ =” xảy ra khi {y−2021=0√x−3−12√y−2021=0
Suy ra {y=2021√x−3−12√y−2021=0
Nên {y=2021x=3 (thỏa mãn)
Vậy biểu thức A đạt giá trị nhỏ nhất bằng 2024 khi x = 3, y = 2021.
Câu 15: Tìm x, y nguyên thỏa mãn: x2 + 2xy + 7(x + y) + 2y2 + 10 = 0.
Lời giải:
Ta có: x2 + 2xy + 7(x + y) + 2y2 + 10 = 0
⟺ 4x2 + 8xy + 28x + 28y + 8y2 + 40 = 0
⟺ (4x2 + 8xy + 28x + 28y + 4y2 + 49) + 4y2 - 9 = 0
⟺ (2x + 2y + 7)2 + 4y2 = 9 (*)
Vì (2x + 2y + 7)2 ≥ 0
Nên 4y2 ≤ 9
Suy ra y2 ≤ 94
Mà y nguyên nên y2∈{0;1}
Suy ra y∈{0;1;−1}
+) Với y = 0, thay vào (*) ta có (2x + 2.0 + 7)2 + 4.0 = 9
Hay (2x + 7)2 = 9
Suy ra [2x+7=32x+7=−3 ⟹ [x=−2x=−5
+) Với y = 1, thay vào (*) ta có (2x + 2.1 + 7)2 + 4.12 = 9
Hay (2x + 9)2 = 5
Suy ra không tìm được x nguyên thỏa mãn.
+) Với y = –1, thay vào (*) ta có (2x – 2.1 + 7)2 + 4. (–1)2 = 9
Hay (2x + 5)2 = 5
Suy ra không tìm được x nguyên thỏa mãn.
Vậy (x; y) = {(-2; 0); (-5; 0)}.
Câu 16: Cho x, y thỏa mãn x2 + 2xy + 7(x + y) + 2y2 + 10 = 0.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức S = x + y + 1.
Lời giải:
Ta có: x2 + 2xy + 7(x + y) + 2y2 + 10 = 0
⟺ (x2 + 2xy + y2) + 7(x + y) + 10 = – y2
⟺ (x + y)2 + 2(x + y) + 5(x + y) + 10 = – y2
⟺ (x + y)(x + y + 2) + 5(x + y + 2) = – y2
⟺ (x + y + 2)(x + y + 5) = – y2
Vì – y2 ≤ 0
Nên (x + y + 2)( x + y + 5) ≤ 0
Suy ra {x+y+2≤0x+y+5≥0⇒{x+y≤−2x+y≥−5
⇒ – 5 ≤ x + y ≤ – 2
⇒ – 4 ≤ x + y + 1 ≤ – 1
Hay – 4 ≤ S ≤ – 1
Nên S đạt giá trị nhỏ nhất bằng – 4 khi {y=0x+y+5=0⇒{y=0x=−5
S đạt giá trị lớn nhất bằng – 1 khi {y=0x+y+2=0⇒{y=0x=−2
Vậy giá trị lớn nhất của S là – 1 khi x = – 2, y = 0; giá trị nhỏ nhất của S là – 4 khi x = – 5, y = 0.
Câu 17: Cho dãy số (un) với un = an2n+1 (a: hằng số); un+1 là số hạng nào sau đây ?
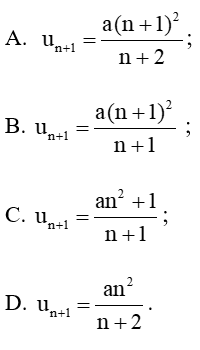
Lời giải:
Đáp án đúng là: A
Ta có: un+1=a(n+1)2(n+1)+1=a(n+1)2n+2
Vậy ta chọn đáp án A.
Câu 18: Cho x ≠ 0, biểu thức nào sau đây có nghĩa?
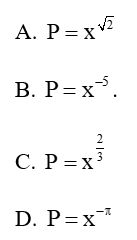
Lời giải:
Đáp án đúng là: B
Ta có: x√2;x−5;x−π có nghĩa khi x > 0
x-5 có nghĩa khi x ≠ 0
Vậy ta chọn đáp án B.
Câu 19: Cho x > 0, biểu thức nào sau đây có nghĩa?
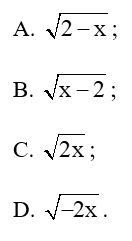
Lời giải:
Đáp án đúng là: C
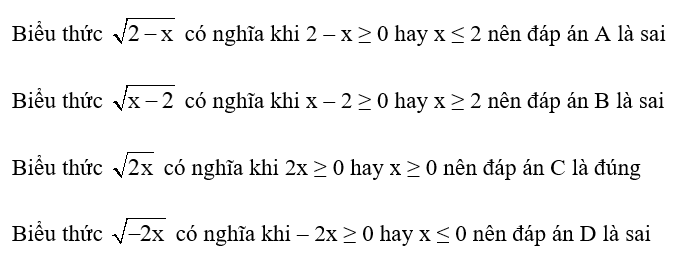
Vậy ta chọn đáp án C.
Câu 20: Cho hàm số y = (2m – 3).x + m – 5. Tìm m để đồ thị hàm số:
a) tạo với 2 trục tọa độ một tam giác vuông cân
b) cắt đường thẳng y = 3x – 4 tại một điểm trên Oy
c) cắt đường thẳng y = – x – 3 tại một điểm trên Ox.
Lời giải:
a) Gọi giao điểm của đồ thị hàm số với trục Ox là A
Suy ra A(5−m2m−3;0) nên OA = |5−m2m−3| ; (m ≠ 32 )
Gọi giao điểm của đồ thị hàm số với trục Oy là B
Suy ra B(0; m – 5) nên OB = |m−5|
Ta có tam giác AOB vuông tại O.
Để tam giác AOB vuông cân tại O thì OA = OB
Hay |5−m2m−3| = |m−5|
⇒[5−m2m−3=m−55−m2m−3=5−m⇔[2m−3=−12m−3=1⇔[2m=22m=4⇔[m=1m=2 (thỏa mãn)
Vậy m = 1 hoặc m = 2 thì đồ thị hàm số tạo với 2 trục tọa độ một tam giác vuông cân
b) Đồ thị hàm số cắt đường thẳng y = 3x – 4 tại một điểm trên Oy
Suy ra giao điểm B(0; m – 5) của đồ thị hàm số đã cho và Oy thuộc đường thẳng y = 3x – 4
Nên m – 5 = 3.0 – 4
Hay m = 1
Vậy m = 1 thì đồ thị hàm số cắt đường thẳng y = 3x – 4 tại một điểm trên Oy
c) Đồ thị hàm số cắt đường thẳng y = – x – 3 tại một điểm trên Ox
Suy ra giao điểm A(5−m2m−3;0) của đồ thị hàm số đã cho và Ox thuộc đường thẳng y=–
Nên
⇔ m – 5 = 3.(2m – 3)
⇔ m – 5 = 6m – 9
⇔ – 5m = – 4
Vậy thì đồ thị hàm số cắt đường thẳng y = – x – 3 tại một điểm trên Ox.
Lời giải:
Gọi giao điểm của đồ thị hàm số với trục Ox là A
Suy ra nên ; (m ≠ 2)
Gọi giao điểm của đồ thị hàm số với trục Oy là B
Suy ra B(0; m – 1) nên OB =
Ta có tam giác AOB vuông tại O. Để tam giác AOB vuông cân tại O thì OA = OB
Hay ; (m ≠ 2, m ≠ 1)
Mà m ≠ 2, m ≠ 1 nên m = 3
Vậy m = 3 thì đồ thị hàm số tạo với 2 trục tọa độ một tam giác vuông cân.
Câu 22: Cho a, b, c đôi một khác nhau thỏa mãn
Tính giá trị của biểu thức .
Lời giải:
Áp dụng tính chất dãy tỉ số bằng nhau ta có
Khi đó P = (1 + 1). (1 + 1). (1 + 1) = 2. 2. 2 = 8
Vậy P = 8.
Câu 23: Cho a, b, c đôi một khác nhau thỏa mãn (a + b + c)2 = a2 + b2 + c2.
Tính .
Lời giải:
Ta có (a + b + c)2 = a2 + b2 + c2
⇔ a2 + b2 + c2 + 2ab + 2bc + 2ac = a2 + b2 + c2
⇔ 2ab + 2bc + 2ac = 0
⇔ ab + bc + ac = 0
⇔
Thay vào biểu thức P ta có
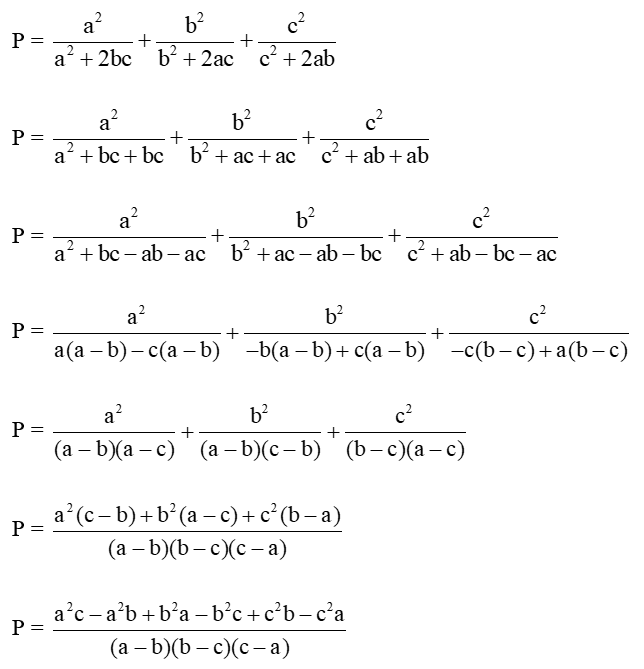
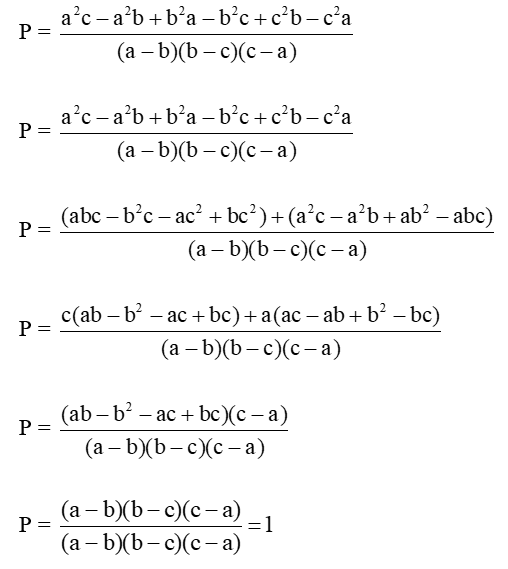
Vậy P = 1.
A. Tam giác MNE.
B. Tứ giác MNEF với F là trung điểm BD.
C. Hình bình hành MNEF với F là điểm trên cạnh BD mà EF // BC.
D. Hình thang MNEF với F là điểm trên cạnh BD mà EF // BC.
Lời giải:
Đáp án đúng là: D
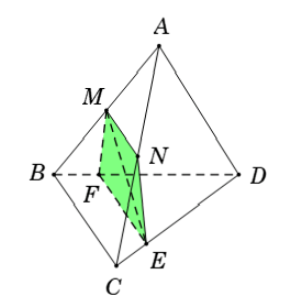
Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC
Nên MN là đường trung bình của tam giác ABC
Suy ra MN // BC
Vì MN // BC, E là điểm chung
Nên giao tuyến của mp(MNE) và mp(BCD) là Ex
Gọi F là giao điểm của Ex và BD
Do đó MN // FE
Suy ra 4 điểm M, N, E, F đồng phẳng và MNEF là hình thang
Vậy hình thang MNEF là thiết diện cần tìm.
Lời giải:
Cách 1:
12 chiếc bút có giá là:
12 × 1 500 = 18 000 (đồng)
35 hộp bút có giá là:
35 × 18 000 = 630 000 (đồng)
Cách 2:
35 hộp bút có số bút là:
35 × 12 = 420 (chiếc)
Mua 35 hộp bút hết số tiền là:
420 × 1 500 = 630 000 (đồng)
Vậy mua 35 hộp bút đó hết 630 000 đồng.
Câu 26: Tìm tập xác định D của hàm số
A. D = (– ∞; 0) ∪ (1; + ∞).
B. D = ℝ \ {0; 1}.
C. D = ℝ.
D. D = (0; 1).
Lời giải:
Đáp án đúng là: B
Hàm số xác định khi và chỉ khi
x3 – x2 ≠ 0
⟺ x2 (x – 1) ≠ 0
⟺
Hay D = ℝ ∖ {0; 1}
Vậy ta chọn đáp án B.
Câu 27: Tìm tập xác định của hàm số
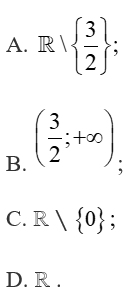
Lời giải:
Đáp án đúng là: A
Hàm số xác định khi và chỉ khi
2x – 3 ≠ 0
Hay tập xác định của hàm số là
Vậy ta chọn đáp án A.
Câu 28: Cho hình bình hành ABCD . Chứng minh
Lời giải:
Vì ABCD là hình bình hành
Nên
Ta có
Vậy .
Câu 29: Cho ba điểm A, B, C. Chứng minh: .
Lời giải:
Với ba điểm A, B, C bất kì ta có:
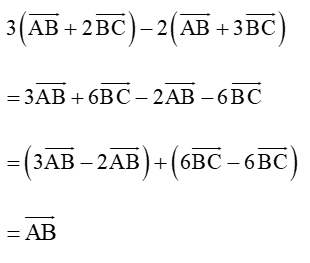
Vậy .
a) 372,95 : 3.
b) 757,5 : 35.
c) 431,25 : 125.
d) 35,1 : 15.
Lời giải:
a) 372,95 : 3 = 124,316666666….
b) 757,5 : 35 = 21,6428571…
c) 431,25 : 125 = 3,45.
d) 35,1 : 15 = 2,34.
Lời giải:
• Để (d1): y = (a – 1)x + 1 và (d2): y = (3 – a)x + 2 cắt nhau thì a – 1 ≠ 3 – a
Û 2a ≠ 4 Û a ≠ 2.
• Để (d1) cắt trục hoành thì a – 1 ≠ 0 Û a ≠ 1.
Gọi A(xA; 0) là giao điểm của (d1) với trục hoành.
Khi đó 0 = (a – 1)xA + 1
Þ . Suy ra .
• Để (d2) cắt trục hoành thì 3 – a ≠ 0 Û a ≠ 3.
Gọi B(xB; 0) là giao điểm của (d2) với trục hoành.
Khi đó 0 = (3 – a)xB + 2
Þ . Suy ra .
Để (d1) và (d2) cắt nhau tại 1 điểm trên trục hoành thì A trùng B.
Þ ‒1.(a – 3) = 2.(a – 1)
Û ‒a + 3 = 2a – 2
Û ‒3a = ‒5
Û (thỏa mãn).
Vậy thỏa mãn yêu cầu đề bài
Lời giải:
• Để (d1): y = (2m + 1)x – 2m – 3 và (d2): y = (m – 1)x + m cắt nhau thì 2m + 1 ≠ m – 1
Û m ≠ ‒2.
• Để (d1) cắt trục hoành thì 2m + 1 ≠ 0 Û .
Gọi A(xA; 0) là giao điểm của (d1) với trục hoành.
Khi đó 0 = (2m + 1)xA – 2m – 3
Þ . Suy ra .
• Để (d2) cắt trục hoành thì m – 1 ≠ 0 Û m ≠ 1.
Gọi B(xB; 0) là giao điểm của (d2) với trục hoành.
Khi đó 0 = (m – 1)xB + m
Þ . Suy ra .
Để (d1) và (d2) cắt nhau tại 1 điểm trên trục hoành thì A trùng B.
Þ (2m + 3).(m – 1) = (2m + 1).(‒m)
Û 2m2 + m – 3 = –2m2 – m
Û 4m2 + 2m – 3 = 0
Û (thỏa mãn).
Vậy thỏa mãn yêu cầu đề bài
Câu 33: Trong phép tính 121,23 : 14 và có thương là 8,65 vậy số dư là bao nhiêu?
A. 13;
B. 1,3;
C. 0,13;
D. 0,013.
Lời giải:
Đáp án đúng là: C
Ta có: Số bị chia = Số chia × Thương + Số dư
Số dư = Số bị chia – Số chia × Thương
= 121,23 – 14 × 8,65
= 121,23 – 121,1
= 0,13.
Câu 34: Tìm số dư của phép chia 121,23 : 14 biết thương lấy đến hai chữ số ở phần thập phân.
Lời giải:
Đặt tính chia: 121,23 : 14 như sau:
Vậy số dư cần tìm là: 0,13.
Câu 35: Cho a + b = 1 và ab ≠ 0. Chứng minh .
Lời giải:
Với a + b = 1 và ab ≠ 0 ta có:
Câu 36: Tính m để 3 điểm thẳng hàng:
a) A(2; 5), B(3; 7), C(2m + 1; m);
b) A(2m; ‒5), B(0; m), C(2; 3);
c) A(3; 7), B(m2; m), C(‒1; ‒1).
Lời giải:
a) Với A(2; 5), B(3; 7), C(2m + 1; m) ta có:
; .
Để ba điểm A, B, C thẳng hàng thì cùng phương
Û 1.(m – 7) = 2.(2m – 2)
Û 3m = ‒3
Û m = ‒1.
b) Với A(2m; ‒5), B(0; m), C(2; 3) ta có:
; .
Để ba điểm A, B, C thẳng hàng thì cùng phương
Û ‒2m.(3 – m) = (m + 5).2
Û ‒3m + m2 = m + 5
Û m2 – 4m – 5 = 0
Û
c) Với A(3; 7), B(m2; m), C(‒1; ‒1) ta có:
; .
Để ba điểm A, B, C thẳng hàng thì cùng phương
Û ‒4.(‒1 – m) = ‒8.(‒1 – m2)
Û 1 + m = 2 + 2m2
Û 2m2 – m + 1 = 0 (vô nghiệm)
Vậy không có giá trị nào của m thỏa mãn.
Câu 37: Tìm m để ba điểm A(2; ‒1), B(1; 1), C(3; m +1) thẳng hàng.
Lời giải:
Giả sử phương trình đường thẳng d đi qua hai điểm A và B có dạng y = ax + b (d).
Do A(2; ‒1) ∈ (d) nên 2a + b = ‒1
Do B(1; 1) ∈ (d) nên a + b = 1
Ta có hệ phương trình
Do đó phương trình đường thẳng d là y = ‒2x + 3.
Để ba điểm A, B và C(3; m +1) thẳng hàng thì điểm C(3; m +1) thuộc đường thẳng d.
Do đó m + 1 = ‒2.3 + 3
Û m = ‒4.
Vậy m = ‒4.
Câu 38: Phương trình ax2 + bx + c = 0 (a ≠ 0) có hai nghiệm phân biệt x1, x2 khác 0 khi nào?
Lời giải:
Để phương trình ax2 + bx + c = 0 (a ≠ 0) có hai nghiệm phân biệt x1, x2 khác 0 thì:
Lời giải:
Đổi 12 kg = 12 000 g.
Không tính vỏ thì can nặng số kg là:
12 000 – 600 = 11 400 (g).
Số nước người ta đổ bớt đi là:
Sau khi đổ bớt nước ra ngoài, can nước nặng là:
12 000 – 3 800 = 8 200 (g).
Đáp số: 8 200 gam.
A.8 kg;
B. 8,2 kg;
C. 820 dag;
D.800 dag.
Lời giải:
Đáp án đúng là: B
Đổi 12 kg = 12 000 g.
Không tính vỏ thì can nặng số kg là:
12 000 – 600 = 11 400 (g).
Số nước người ta đổ bớt đi là:
Sau khi đổ bớt nước ra ngoài, can nước nặng là:
12 000 – 3 800 = 8 200 (g) = 8,2 (kg).
A. m = 0;
B. m ∈ ∅;
C. m = 2;
D. .
Lời giải:
Đáp án đúng là: D
D1 ⊥ D2 khi và chỉ khi (2m – 1).3 + m.2 = 0
Û 6m – 3 + 2m = 0
Û 8m = 3
Û .
Lời giải:
Ta có: 58 = 2.29
Do đó Ư(58) = {‒58; ‒29; ‒2; ‒1; 1; 2; 29; 58}.
Lời giải:
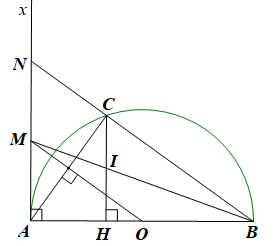
• Gọi N là giao điểm của BC và Ax.
Vì C thuộc đường tròn tâm O đường kính AB nên OA = OB = OC
Do đó DABC vuông tại C nên AC ⊥ BC.
Mà OM ⊥ AC (giả thiết) nên OM // BC hay OM // BN.
Xét DABN có OM // BN và O là trung điểm của AB
Do đó M là trung điểm của AN hay AM = MN.
• Do Ax là tiếp tuyến của (O) nên Ax ⊥ AB
Ta có: CH ⊥ AB, Ax ⊥ AB nên CH // AB.
Xét DABM có IH // AM, theo hệ quả định lí Thalès ta có: .
Xét DMBN có CI // MN, theo hệ quả định lí Thalès ta có: .
Do đó
Mà AM = MN (chứng minh trên) nên IH = CI.
Vậy CI = IH.
Câu 44: Hình thoi ABCD có diện tích 20 cm2 và đường chéo AC bằng 10 cm. Tính độ dài đường chéo BD.
Lời giải:
Diện tích hình thoi ABCD được tính như sau: .
Độ dài đường chéo BD là: .
Câu 45: Tìm tập xác định của hàm số .
Lời giải:
Xét hàm số .
• Với x < 2 ta có
Hàm số xác định .
Kết hợp điều kiện x < 2, ta có: x < 2.
Do đó tập xác định của hàm số trong trường hợp này là (–∞; 2).
• Với x ≥ 2 ta có .
Hàm số xác định
Kết hợp điều kiện x ≥ 2, ta có x ≥ 2
Do đó tập xác định của hàm số trong trường hợp này là [2; +∞).
Vậy kết hợp 2 trường hợp ta có tập xác định của hàm số là D = ℝ.
Câu 46: Cho tam giác ABC nhọn, vẽ đường tròn cắt các cạnh AB, AC theo thứ tự tại D và E.
a) Chứng minh rằng: CD vuông góc với AB, BE vuông góc với AC.
b) Gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc với BC.
Lời giải:
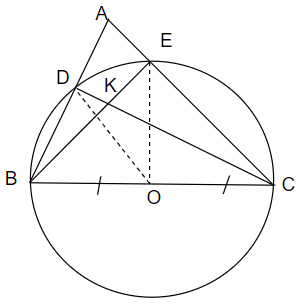
a) Tam giác BCD nội tiếp trong đường tròn (O) có BC là đường kính nên vuông tại D.
Suy ra: CD ⊥ AB.
Tam giác BCE nội tiếp trong đường tròn (O) có BC là đường kính nên vuông tại E.
Suy ra: BE ⊥ AC.
b) Xét ∆ABC có K là giao điểm của hai đường cao CD và BE nên K là trực tâm của tam giác ABC.
Suy ra: AK ⊥ BC.
Lời giải:
Hai đồ thị hàm số y = 2x + (3 + m) và y = 3x + (5 – m) cắt nhau Û 2 ≠ 3 (luôn đúng ∀m).
Do đó hai đồ thị đã cho luôn cắt nhau.
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
2x + (3 + m) = 3x + (5 – m)
Û 3x – 2x = 3 + m – 5 + m
Û x = 2m – 2
Thay x = 2m – 2 vào y = 2x + (3 + m) ta được:
y = 2(2m – 2) + 3 + m
Û y = 4m – 4 + 3 + m
Û y = 5m – 1.
Do đó tọa độ giao điểm của hai đồ thị hàm số đã cho là (2m – 2; 5m – 1)
Để hai đồ thị hàm số y = 2x + (3 + m) và y = 3x + (5 – m) cắt nhau tại 1 điểm trên trục hoành thì 5m – 1 = 0
.
Vậy giá trị m cần tìm là .
Lời giải:
Do gấp thừa số thứ nhất lên 2 lần nên tích mới sẽ gấp lên 2 lần.
Do gấp thừa số thứ hai lên 3 lần nên tích mới sẽ gấp lên 3 lần.
Nếu gấp thừa số thứ nhất lên 2 lần và gấp thừa số thứ hai lên 3 lần thì tích mới gấp lên 2 × 3 = 6 lần.
Vậy tích mới là 625 × 6 = 3750.
Câu 49: Tìm tập xác định của hàm số .
Lời giải:
Để hàm số xác định thì .
Vậy tập xác định của hàm số đã cho là .
Câu 50: Tìm tập xác định của hàm số .
Lời giải:
Để hàm số xác định thì
Vậy tập xác định của hàm số đã cho là D = (2; +∞).
Lời giải:
Giả sử phương trình x3 – 15x2 + 71x – 105 = 0 có ba nghiệm tạo thành cấp số cộng:
a – d; a; a + d (với d ≠ 0).
Khi đó ta có: (a – d)3 – 15(a – d)2 + 71(a – d) – 105 = 0 (1)
a3 – 15a2 + 71a – 105 = 0 (2)
(a + d)3 – 15(a + d)2 + 71(a + d) – 105 = 0 (3)
Từ (1) ta có:
a3 – 3a2d + 3ad2 – d3 – 15a2 + 30ad – 15d2 + 71a – 71d – 105 = 0
Þ – 3a2d + 3ad2 – d3 + 30ad – 15d2 – 71d = 0 (do a3 – 15a2 + 71a – 105 = 0) (*)
Tương tự từ (3) ta có: 3a2d + 3ad2 + d3 – 30ad – 15d2 + 71d = 0 (**)
Cộng (*) với (**) ta được:
6ad2 – 30d2 = 0 Û 6d2(a – 5) = 0
Vì d ≠ 0 nên ta có a – 5 = 0 Û a = 5.
Vì a = 5 là một nghiệm của phương trình đã cho nên vế trái của phương trình chia hết cho (x – 5).
Do đó theo sơ đồ Horner ta có:
x3 – 15x2 + 71x – 105 = 0
Û (x – 5)(x2 – 10x + 21) = 0
Û (x – 5)(x2 – 10x + 21) = 0
Û (x – 5)(x – 3)(x – 7) = 0
Û x = 3 hoặc x = 5 hoặc x = 7.
Vậy các nghiệm của phương trình đã cho là: .
Lời giải:
Phương trình hoành độ giao điểm của đồ thị hàm số (1) và đường thẳng y = 4x + m là:
2x2 – 3x – 5 = 4x + m
Û 2x2 – 7x – 5 – m = 0 (*)
Để đồ thị hàm số (1) cắt đường thẳng y = 4x + m tại hai điểm phân biệt A(x1; y1), B(x2; y2) thì phương trình (*) phải có hai nghiệm phân biệt x1, x2
Û D > 0
Û (–7)2 – 4.2.(– 5 – m) > 0
Û 49 + 40 + 8m > 0
.
Khi đó, theo hệ thức Viet ta có:
Theo bài,
(thỏa mãn)
Vậy m = –10.
A. 15 cm;
B. 25 cm;
C. 35 cm;
D. 45 cm.
Lời giải:
Đáp án đúng là: B
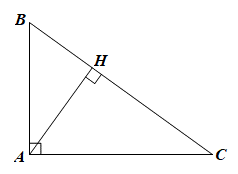
Ta có:
Þ AH.BH.AH.CH = 108.192 = 20 736
Þ AH2.BH.CH = 20 736 (*)
Xét tam giác ABC vuông tại A có đường cao AH, theo hệ thức lượng ta có:
AH2 = BH.CH
Thay vào (*) ta được: AH2.AH2 = 20 736
Þ AH4 = 20 736 = 124
Þ AH = 12 cm.
và
Þ BC = BH + CH = 9 + 16 = 25 (cm).
a) Viết hàm số biểu diễn y theo x.
b) Nếu trường chỉ có thể huy động 15 bạn nam có khả năng làm thì cần huy động thêm bao nhiêu bạn nữ?
Lời giải:
a) Mỗi ngày x bạn nam là được số lồng đèn là: 2x (cái)
Mỗi ngày y bạn nữ làm được số lồng đèn là: 3y (cái).
Tổng số lồng đèn trường A làm được trong một ngày là: 2x + 3y = 120
Þ 3y = 120 – 2x
.
Vậy hàm số biểu diễn y theo x là: .
b) Ta có x = 15, thay vào hàm số biểu diễn y theo x là: ta được:
.
Vậy cần huy động 30 nữ.
Lời giải:
Xét phương trình x2 – (m – 1)x – m = 0
Có D = [–(m – 1)]2 – 4.1.(–m) = m2 – 2m + 1 + 4m = m2 + 2m + 1 = (m + 1)2.
Để phương trình có hai nghiệm phân biệt thì D > 0
Û (m + 1)2 > 0
Û m + 1 ≠ 0
Û m ≠ –1 (1)
Theo định lí Viet ta có:
Để phương trình có hai nghiệm đều nhỏ hơn 1 thì
(2)
Từ (1) và (2) ta có: m < 1; m ≠ –1.
Vậy m < 1 và m ≠ –1.
Câu 56: Tìm m để ba đường thẳng đồng quy.
Lời giải:
Các bước giải bài toán tìm m để ba đường thẳng đồng quy:
Bước 1: Tìm điều kiện để các đường thẳng cắt nhau.
Bước 2: Tìm giao điểm của hai đường thẳng (hai đường thẳng không chứa m).
Bước 3: Để ba đường thẳng đồng quy thì giao điểm đã tìn được ở Bước 2 phải thỏa mãn khi thay vào phương trình đường thẳng còn lại. Từ đó suy ra giá trị tham số m.
Lời giải:
Phương trình hoành độ giao điểm của (d1) và (d2) là:
x + 6 = 3x + 7
Û 2x = –1
.
Với thì .
Suy ra hai đường thẳng (d1) và (d2) cắt nhau tại điểm .
Để (d1), (d2) và (d3) đồng quy thì (d3) phải đi qua giao điểm của (d1) và (d2).
Khi đó ta có:
Vậy với m = 11 thì ba đường thẳng đã cho đồng quy.
Câu 58: Nêu công thức tính số đo góc giữa hai vectơ.
Lời giải:
Công thức tính góc giữa hai vectơ dựa vào tích vô hướng: .
Câu 59: Chứng minh rằng a3b – ab3 chia hết cho 6 với mọi số nguyên a và b.
Lời giải:
Ta có: a3b – ab3
= a3b – ab – ab3 + ab
= ab(a2 – 1) – ab(b2 – 1)
= ab(a – 1)(a + 1) – ab(b – 1)(b + 1)
Mà 3 số tự nhiên liên tiếp luôn chia hết cho 6 nên ta có:
(a – 1).a.(a + 1) ⋮ 6 và (b – 1).b.(b + 1) ⋮ 6
Suy ra ab(a – 1)(a + 1) – ab(b – 1)(b + 1) ⋮ 6
Vậy a3b – ab3 chia hết cho 6 với mọi a, b.
Lời giải:
Ta có: CD = 2CN và N nằm trên cạnh CD nên .
Mà ABCD là hình bình hành nên
Do đó .
Suy ra .zư
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.