Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 89) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 89)
Câu 1: Đúng ghi Đ sai ghi S:
a) 418 cm = 41,8 m.
b) 53 cm = 0,53 m.
c)105 cm = 1,05 m.
d) 908 dm = 9,08 m.
Lời giải:
a) S (100cm = 1m nên 418cm = 4,18m)
b) Đ (100cm = 1m nên 53cm = 0,53m)
c) Đ (100cm = 1m nên 105cm = 1,05m)
d) S (10dm = 1m nên 908dm = 90,8m).
Câu 2: x – y và y – x có giống nhau không? Vì sao?
Lời giải:
x – y và y – x không giống nhau
Đây là 2 số đối nhau vì x – y + y – x = 0.
Câu 3: A, B và C chạy quanh một đường tròn có chiều dài 750m với tốc độ lần lượt là 3 m/giây, 6m/giây và 18m/giây. Nếu cả ba bắt đầu từ cùng một điểm, đồng thời và chạy theo cùng một hướng, khi nào họ sẽ gặp nhau lần đầu tiên sau khi họ bắt đầu cuộc đua?
Lời giải:
S = 750m
V1 = 3m/s
V2 = 6m/s
V3 = 18m/s
V = ƯC (3; 6; 18)
Mà: 3 = 3; 6 = 2.3; 18 = 2.32
Thời gian họ gặp nhau lần đầu tiên là:
t = S : V = 750 : 3 = 250 (giây).
Câu 4: Một cửa hàng nhập về 50 chiếc túi xách với giá góc 150 000 đồng/cái. Cửa hàng đã bán 30 chiếc với giá mỗi chiếc lãi 30% so với giá gốc, 20 chiếc còn lại bán lỗ 5% so với giá gốc. Hỏi sau khi bán hết 50 chiếc túi xách cửa hàng đó lãi hay lỗ bao nhiêu tiền?
Lời giải:
Giá vốn 50 chiếc túi xách:
50.150000 = 7500000 (đồng)
Giá bán để cửa hàng lãi 30% so với giá gốc là:
150000.(100% + 30%) = 150000.130% = 195000 (đồng)
Số tiền thu được khi bán với giá lãi 30%:
30.195000 = 5850000 (đồng)
Giá bán làm cửa hàng lỗ 5% so với giá gốc là:
150000.(100% − 5%) = 150000.95% = 142500 (đồng)
Số tiền thu được khi bán với giá lỗ 5%:
20.142500 = 2850000 (đồng)
Tổng tiền thu được:
5850000 + 2850000 = 8700000 > 7500000
Vậy cửa hàng lãi và lãi: 8700000 − 7500000 = 1200000 (đồng).
Câu 5: Một ô tô cứ đi 100km thì tiêu thụ hết 12,5 lít xăng. Hỏi ô tô đó đi quãng đường dài 60km thì tiêu thụ hết bao nhiêu xăng ?
Lời giải:
1km thì ô tô đó tiêu thụ hết số lít xăng là:
12,5 : 100 = 0,125 (lít).
60km thì ô tô tiêu thụ hết số lít xăng là:
60 . 0,125 = 7,5 (lít).
Đáp số: 7,5 lít.
Câu 6: Tính chiều cao của cây trong hình vẽ bên (Làm tròn đến chữ số thập phân thứ nhất).
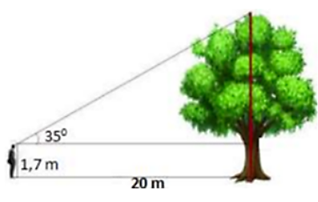
Lời giải:
Chiều cao của cây là: h = 1,7 + 20. tan35o ≈ 15,7 m.
Câu 7: Tìm n biết: (n – 3) + (n – 2) + (n – 1) + .... + 10 + 11 = 11.
Lời giải:
(n – 3) + (n – 2) + (n – 1) + .... + 10 + 11 = 11
⇔ (n – 3) + (n – 2) + (n – 1) + .... + 10 = 0
Gọi số các số hạng từ n – 3 đến 10 là x
Ta có: [10 + (n – 3)].x : 2 = 0
⇔ (n + 7)x = 0
Vì x khác 0 do x là số các số hạng
Nên n + 7 = 0
Suy ra: n = – 7
Vậy n = –7.
Câu 8: Tính: 99 + (–5) + (–104) + 11.
Lời giải:
99 + (–5) + (–104) + 11
= (99 + 11) + [(–5) + (–104)]
= 110 + (–109)
= 110 – 109
= 1.
Câu 9: Tính nhanh: [(–59) + 71] – [–83 – (–95)].
Lời giải:
[(–59) + 71] – [–83 – (–95)]
= (71 – 59) – (–83 + 95)
= 12 – 12
= 0.
Câu 10: Cho a = –13; b = 25; c = –30. Tính giá trị biểu thức:
a) a + a + 12 – b.
b) a + b – (c + b).
c) 25 + a – (b + c) – a.
Lời giải:
a) a + a + 12 – b = 2a + 12 – b = 2.(–13) + 12 – 25 = –26 + 12 – 25 = –29.
b) a + b – (c + b) = a + b – c – b = a – c = –13 – (–30) = 30 – 13 = 17.
c) 25 + a – (b + c) – a = 25 – b – c = 25 – 25 – (–30) = 30.
Câu 11: Cho hình vuông có chu vi 20cm. Nếu kéo dài mỗi cạnh của hình vuông thêm 3cm thì hình vuông mới có chu vi là bao nhiêu ?
Lời giải:
Cạnh của hình vuông đó là:
20 : 4 = 5 (cm)
Nếu kéo dài mỗi cạnh hình vuông 3cm thì độ dài cạnh hình vuông mới là:
5 + 3 = 8 (cm)
Chu vi hình vuông mới là:
8 . 4 = 32 (cm).
Câu 12: Cho một số tự nhiên gồm các số tự nhiên liên tiếp từ 1 đến 2020, được viết theo thứ tự liền nhau như sau: 1 2 3 4 5 6 7 8 9 10 11 12 13 … 2017 2018 2019 2020 2021. Hãy tính tổng tất cả các chữ số của số đó?
Lời giải:
Bước 1: Tính tổng các chữ số từ 0 đến 999:
Thêm các chữ số 0 vào trước các số có 1 và 2 chữ số để ta được dãy số gồm toàn các số có 3 chữ số: 000; 001; 002; 003; 004; ...; 999 (Tổng các chữ số vẫn không thay đổi)
Khi này, dãy số trên có 1000 số
Số các chữ số là: 1000 × 3 = 3 000 (chữ số)
Mỗi chữ số 0; 1; 2; ...; 9 xuất hiện số lần là: 3000 : 10 = 300 (lần)
Vậy, tổng các chữ số từ 0 đến 999 là:
(0 + 1 + 2 + ... + 9) . 300 = 45 . 300 = 13 500
Bước 2: Tính tổng các chữ số từ 1000 đến 1999:
So với dãy số 000 đến 999 thì mỗi số tăng thêm 1 ở hàng nghìn
Vậy tổng các chữ số từ 1000 đến 1999 là:
13500 + 1 . 1000 = 13500 + 1000 = 14500
Bước 3: Tính tổng các chữ số từ 2000 đến 2021:
Ta có tổng các chữ số từ 2000 đến 2021 là:
(2 . 21 + 1 . 10 + 2 + 2 . 45) + (2 + 0 + 2 + 1)
= (42 + 10 + 2 + 90) + 5
= 144 + 5
= 149
Vậy, tổng tất cả các chữ số từ 1 đến 2021 là 13 500 + 14500 + 149 = 28149.
Câu 13: Biết đồ thị hàm số y = (k – 3)x – 4 cắt đường thẳng y = –3x + 2 tại điểm có tung độ bằng 5. Tìm tham số k?
Lời giải:
Điểm có tung độ bằng 5 là A(0,5)
⇒ 5 = −3x + 2
⇒ x = −1
Thay x, y vào y = (k − 3)x − 4
⇔ 5 = (k − 3)⋅(−1) – 4
⇔ k = −6
Vậy k = –6.
Câu 14: Hình chữ nhật có chiều dài và chiều rộng cùng tăng 4 lần thì diện tích của nó tăng lên bao nhiêu lần?
Lời giải:
Nếu trong 1 hình chữ nhật, có chiều dài và chiều rộng cùng tăng lên 4 lần thì diện tích tăng:
4 . 4 = 16 (lần).
Câu 15: Lớp 11A1 có 41 học sinh trong đó có 21 bạn nam và 20 bạn nữ. Thứ hai đầu tuần lớp phải xếp hàng chào cờ thành một hàng dọc. Hỏi có bao nhiêu cách sắp xếp để 21 bạn nam xen kẽ với 20 bạn nữ?
Lời giải:
Vì số học sinh nam là lẻ nên bạn nam phải đứng đầu hàng.
Khi đó xếp 21 bạn nam vào 21 vị trí cố định có: 21! = P21 (cách).
Sau đó ta xếp 20 bạn nữ vào 20 vị trí trống xen kẽ với các bạn nam thì sẽ có:
20! = P20 (cách).
Câu 16: Một hình bình hành ABCD có diện tích 350 cm2, biết độ dài đường cao AH = 35 cm. Tính độ dài cạnh AB.
Lời giải:
Ta có diện tích của hình bình hành là:
SABCD = AH.AB
35.AB = 350
⇔ AB = 350 : 35 = 10 (cm)
Vậy AB = 10 cm.
Câu 17: Tính giá trị biểu thức: (–167) . (67 – 34).
Lời giải:
(–167) . (67 – 34)
= (–167) . 33
= –5511.
Câu 18: Bỏ ngoặc rồi tính: (123 – 27) + (27 + 13 – 123).
Lời giải:
(123 − 27) + (27 + 13 − 123)
= 123 – 27 + 27 + 13 − 123
= 13(123 − 27) + (27 + 13 − 123)
= 123 – 27 + 27 + 13 – 123
= 13.
Câu 19: Một hình thoi có diện tích là 20cm2, biết độ dài một đường chéo là 20 cm. Tính độ dài đường chéo còn lại.
Lời giải:
Độ dài đường chéo còn lại là:
20 . 2 : 20 = 2 (cm)
Đáp số : 2cm.
Câu 20: Tìm phép dư trong phép chia đa thức f(x) = x2020 – 1 cho đa thức g(x) = x2 + x + 1.
Lời giải:
f(x) = x2020 – 1 = (x2020 – x) + x – 1 = x(x2019 – 1) + (x – 2)
= x[(x3)673 – 1673] + x – 1
Do (x3)673 – 1673 chia hết cho x3 – 1
Suy ra: x[(x3)673 – 1673] chia hết cho x3 – 1 mà cho x3 – 1 chia hết cho x2 + x + 1
Do đó f(x) chia g(x) có số dư là x – 1.
Câu 21: Tìm x biết: (x – 12) – 15 = 20 – (17 + x).
Lời giải:
(x – 12) – 15 = 20 – (17 + x)
⇔ x – 12 – 15 = 20 – 17 – x
⇔ x – 27 = 3 – x
⇔ 2x = 3 + 27
⇔ 2x = 30
⇔ x = 30 : 2
⇔ x = 15
Vậy x = 15.
Câu 22: Tìm x biết: 720 : [41 – (2x – 5)] = 23.5.
Lời giải:
720 : [41 – (2x – 5)] = 23.5
⇔ 720 : [41 – (2x – 5)] = 8.5
⇔ 720 : [41 – (2x – 5)] = 40
⇔ 41 – (2x – 5) = 720 : 40
⇔ 41 – (2x – 5) = 18
⇔ 46 – 2x = 18
⇔ 2x = 46 – 18
⇔ 2x = 28
⇔ x = 28 : 2
⇔ x = 14
Vậy x = 14.
Câu 23: 90000m2 =… hm2.
Lời giải:
1 hm2 = 10000 m2
90000m2 = 9 hm2
Câu 24: Biểu đồ dưới đây nói về số học sinh tham gia tập bơi của khối lớp Bốn ở một trường tiểu học :
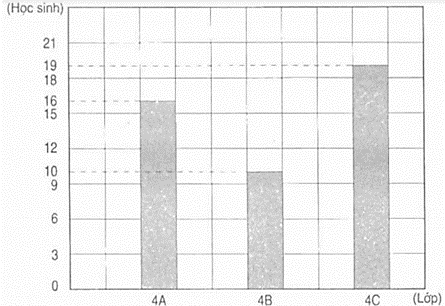
Dựa vào biểu đồ dưới đây hãy viết vào chỗ chấm :
a) Lớp 4A có ……… học sinh tập bơi
b) Lớp 4B có ……… học sinh tập bơi
c) Lớp ……… có nhiều học sinh tập bơi nhất
d) Số học sinh tập bơi của lớp 4B ít hơn lớp 4A là ………học sinh
e) Trung bình mỗi lớp có ……… học sinh tập bơi.
Lời giải:
a) Lớp 4A có 16 học sinh tập bơi
b) Lớp 4B có 10 học sinh tập bơi
c) Lớp 4C có nhiều học sinh tập bơi nhất
d) Số học sinh tập bơi của lớp 4B ít hơn lớp 4A là 6 học sinh
e) Trung bình mỗi lớp có 15 học sinh tập bơi.
Câu 25: Phân tích các số sau ra thừa số nguyên tố và tìm xem mỗi số có bao nhiêu ước:
a) 320
b) 625
c) 504
d) 900
e) 3675.
Lời giải:
a) 320 = 26 . 5
Số ước của 320 = (6 + 1)(1 + 1) = 14
b) 625 = 54.
Suy ra 625 có 4 + 1 = 5 ước.
c) 504 = 23.32.7.
Suy ra 504 có (3 + 1)(2 + 1)(1 + 1) = 24 ước.
d) 900 = 22.32.52.
Suy ra 900 có (2 + 1)(2 + 1)(2 + 1) =27 ước.
e) 3675 = 3.52.72.
Suy ra 3675 có (1 + 1)(2 + 1)(2 + 1) = 18 ước.
Câu 26: Tìm x biết: –x – 14 + 32 = – 26.
Lời giải:
–x – 14 + 32 = –26
⇔ –x = –26 – 32 + 14
⇔ –x = –44
⇔ x = 44
Vậy x = 44.
Câu 27: Tìm x biết: 2x(3x + 5) – x(6x – 1) = 33.
Lời giải:
2x(3x + 5) – x(6x – 1) = 33
⇔ 6x2 + 10x – 6x2 + x – 33 = 0
⇔ 11x = 33
⇔ x = 33 : 11
⇔ x = 3
Vậy x = 3.
Câu 28: Một đoàn tàu dài 280m chạy qua một đường hầm dài 1200m trong 2 phút 30 giây với vận tốc đó tàu chạy quãng đường 159,84 km trong thời gian bao lâu?
Lời giải:
Đổi 2 phút 30 giây = 2,5 phút
Vận tốc đoàn tàu đó là:
1200 : 2,5 = 480 (m/phút)
Đổi 159,84 km = 159840 m
Với vận tốc đó tàu chạy quãng đường 159,84 km trong số thời gian là:
159 840 : 480 = 333 (phút).
Câu 29: Phân tích đa thức thành nhân tử: (3x + 2)(3x – 5)(x – 1)(9x + 10) + 24x2.
Lời giải:
(3x + 2)(3x – 5)(x – 1)(9x + 10) + 24x2
= (9x2 – 9x – 10)(9x2 + x – 10) + 24x2
Đặt 9x2 – 10 = a
Ta có: (a – 9x)(a + x) + 24x2
= a2 – 9xa + ax – 9x2 + 24x2
= a2 – 8ax + 15x2
= a2 – 5ax – 3ax + 15x2
= a(a – 5x) – 3x(a – 5x)
= (a – 5x)(a – 3x)
= (9x2 –5x – 10)(9x2 – 3x – 10)
Câu 30: Tìm ba số hạng liên tiếp của một cấp số cộng, biết rằng tổng của chúng bằng 15 và tích của chúng bằng 105.
Lời giải:
Gọi 3 số hạng liên tiếp của 1 cấp số cộng đó lần lượt là a, a+d và a+2d ( d là công sai)
Vì tổng của chúng bằng 15 , ta có:
a + a + d + a + 2d = 15
⇒ 3a + 3d = 15
⇒ 3.(a + d) = 15
⇒ a + d = 5
Vậy số hạng thứ 2 là 5 và d = 5–a
Vì tích của chúng bằng 105
⇒ a.(a + d).(a + 2d) = 105
⇔ 5a.(a + 2d) = 105
⇔ a.(a + 2d) = 21
⇔ a2 + 2ad = 21
⇔ a2 + 2.a.(5 − a) = 21
⇔ a2 + 10a−2a2 = 21
⇔ −a2 + 10a – 21 = 0
⇔ a2 − 10a + 21 = 0
⇔ a = 7 hoặc a = 3
⇒ d = –2 hoặc d = 2
Vậy 3 số đó lần lượt là 7, 5, 3 hoặc 3, 5, 7.
Câu 31: Tính chu vi và diện tích của mảnh đất hình chữ nhật biết chiều rộng của mảnh đất là 8,5m, chiều dài gấp đôi chiều rộng.
Lời giải:
Chiều dài mảnh đất là:
8,5 . 2 = 17(m)
Chu vi mảnh đất là:
(17 + 8,5) . 2 = 51 (m)
Diện tích mảnh đất là:
17 . 8,5 = 144,5 (m2).
Câu 32: Tìm x biết: (2x + 3)2 – 4x(x + 4) = 25.
Lời giải:
(2x + 3)2 – 4x(x + 4) = 25
⇔ 4x2 + 12x + 9 – 4x2 – 16x – 25 = 0
⇔ –4x = 16
⇔ x = –4
Vậy x = –4.
Câu 33: 245 phút = …giờ… phút.
Lời giải:
Lấy 245 : 24 = 10 dư 5
Suy ra: 245 phút = 10 giờ 5 phút.
Câu 34: Bỏ ngoặc rồi tính 25 − ( − 17 ) + 24 – 12.
Lời giải:
25 − ( − 17 ) + 24 – 12
= 25 + 17 + 24 – 12
= 54.
Câu 35: Tìm nghiệm nguyên của phương trình: 3x2 – 2xy + y – 5x + 2 = 0.
Lời giải:
3x2 – 2xy + y – 5x + 2 = 0
⇔ 12x2 –8xy + 4y – 20x + 8 = 0
⇔ (4y − 8xy) − (6x − 12x2) + (7 − 14x) + 1 = 0
⇔ 4y.(1−2x) − 6x.(1 − 2x) + 7.(1 − 2x) = −1
⇔ (1 − 2x).(4y − 6x + 7) = −1
Do x, y nguyên nên 1 – 2x và 4y – 6x + 7 nguyên
Do đó: 1 – 2x và 4y – 6x + 7 là cặp ước của – 1
Ta có bảng:
|
1 – 2x |
–1 |
1 |
|
x |
1 |
0 |
|
4y – 6x + 7 |
1 |
–1 |
|
y |
0 |
–2 |
Vậy phương trình có nghiệm (x; y) ∈ {(1; 0); (0; −2)}.
Câu 36: 435 phút = …giờ… phút.
Lời giải:
Lấy 435 : 24 = 18 dư 3
Suy ra: 435 phút = 18 giờ 3 phút.
Câu 37: Phân tích đa thức thành nhân tử: 9x2 – 36xy – 36y2.
Lời giải:
9x2 – 36xy + 36y2
= (3x)2 – 2.3x.6y + (6y)2
= (3x – 6y)2.
Câu 38: Biết rằng tổng của n số tự nhiên đầu tiên là 210, tìm giá trị của n.
Lời giải:
1 + 2 + 3 + ... + n = 210
Dãy trên có số số hạng là:
(n − 1) : 1 + 1 = n (số hạng)
Tổng của dãy trên là:
(n + 1) . n : 2 = 210
⇔ (n+1)n = 420
⇔ (n + 1) n = 21.20
⇔ n = 20
Vậy n = 20.
Câu 39: Số 252 có bao nhiêu ước dương?
Lời giải:
252 = 22.32.7
Số 252 có số ước là:
(2 + 1).(2 + 1).(1 + 1) = 18
Ư(252) = {1; 2; 3; 4; 6; 7; 9; 12; 14; 18; 21; 28; 36; 42; 63; 84; 126; 252}.
Câu 40: 1 người gửi tiết kiệm 50000000 đồng với lãi suất là 0.6%/1 tháng . hỏi sau 1 tháng cả số tiền gửi và tiền lãi là bao nhiêu là bao nhiêu?
Lời giải:
Số tiền nhận được sau 1 tháng chiếm là :
100% + 0.6% = 100,6% (số tiền)
Số tiền nhận được sau 1 tháng là :
50000000 : 100 . 100,6 = 50300000 (đồng).
Đáp số : 50300000 đồng .
Câu 41: Theo biểu giá bán lẻ xăng dầu một lít xăng RON 95 – IV có giá 18000 đồng. Do ảnh hưởng dịch Covid – 19 , giá xăng giảm 20 %. Sau đó lại điều chỉnh giảm giá tiếp 10% . Hỏi sau 2 lần điều chỉnh giá xăng là bao nhiêu?
Lời giải:
Giá tiền xăng giảm giá lúc đầu là:
18000 . (100% – 20%) =14400 (đồng)
Giá tiền xăng sau 2 lần giảm là :
14400 . (100% – 10%) = 12960 (đồng)
Vậy sau 2 lần điều chỉnh giá xăng là 12960 đồng.
Câu 42: Tìm x biết:
a) 2075 : 5 = x . 75 : 5 + 40.
b) x + x : 5 . 7,5 + x : 2 . 9 = 315.
Lời giải:
a) 2075 : 5 = x . 75 : 5 + 40
⇔ 415 = 15x + 40
⇔ 15x = 375
⇔ x = 375 : 15
⇔ x = 25
Vậy x = 25.
b) x + x : 5 . 7,5 + x : 2 . 9 = 315
⇔ x + x . 1,5 + x . 4,5 = 315
⇔ x(1 + 1,5 + 4,5) = 315
⇔ 7x = 315
⇔ x = 315 : 7
⇔ x = 45.
Vậy x = 45.
Câu 43: Tính bằng cách thuận tiện nhất 46 : 24 + 8 : 24.
Lời giải:
46 : 24 + 8 : 24
= (46 + 8) : 24
= 54 : 24
= 2,25
Câu 44: Tìm nghiệm nguyên của phương trình: x2 + x + 2009 = y2.
Lời giải:
x2 + x + 2009 = y2
⇔ 4x2 + 4x + 8036 = 4y2
⇔ (2x + 1)2 + 8035 = (2y)2
⇔ (2y)2 – (2x + 1)2 = 8035
⇒ (2y − 2x − 1)(2y + 2x + 1) = 8035
⇒ (2y − 2x − 1, 2y + 2x + 1) là cặp nghiệm của 8035
Mà 2y − 2x – 1 + 2y + 2x + 1 = 4y ⋮ 4
⇒ (2y − 2x − 1, 2y + 2x + 1) ∈ {(1, 8035); (8035, 1); (5, 1607); (1607, 5); (−1, −8035); (−8035, −1); (−5, −1607); (−1607, −5)}
⇒(2y − 2x, 2y + 2x) ∈ {(2, 8034); (8036, 0); (6, 1606); (1608, 4); (0, −8036); (−8034, −2); (−4, −1608); (−1606, −6)}
⇒(y − x, y + x) ∈ {(1, 4017); (4017, 0); (3, 803); (803, 2); (0, −4017); (−4017, −1); (−2, −8004); (−8004, −3)}.
Vì y – x ; y + x chẵn
⇒ (y − x, y + x) ∈ {(1, 4017); (3, 803); (−4017, −1); (−2, −8004)}
⇒ (2y, 2x) ∈ {(4018, 4016); (806, 800); (−4018, 4016); (−8006, −8002)}
⇒ (y, x) ∈ {(2009, 2008); (403, 400); (−2009, 2008); (−4003, −4001)}.
Câu 45: Tìm cặp số tự nhiên x,y biết: 6xy – 9x – 4y + 5 = 0.
Lời giải:
6xy − 9x − 4y + 5 = 0
⇒ 3x(2y − 3) − 4y + 6 = 1
⇒ 3x(2y − 3) − 2(2y − 3) = 1
⇒ (3x − 2)(2y − 3) = 1
Ta có bảng:
|
3x – 2 |
1 |
–1 |
|
2y – 3 |
1 |
–1 |
|
x |
1 |
|
|
y |
2 |
1 |
Vì x, y là số tự nhiên nên x = 1; y = 2.
Câu 46: Cho các số 13,1; 13,01; 1,30.103; 1.3.10–3. Có mấy số có ba chữ số có nghĩa?
Lời giải:
1,3 . 103 = 1,3 . 1000 = 1300
1,3 . 10–3 = 0,0013
Số có 3 chữ số là 13,1.
Câu 47: Tìm x biết: x + (–62) + (–46) = –14.
Lời giải:
x + (–62) + (–46) = –14
⇔ x – 62 – 46 = –14
⇔ x = 62 + 46 – 14
⇔ x = 94
Vậy x = 94.
Câu 48: Tìm các ước dương của 99.
Lời giải:
99 = 32 . 11
Số ước dương của 99 là: (2 + 1)(1 + 1) = 6 (ước)
Ư(99) = {1; 3; 9; 11; 33; 99}.
Câu 49: Tìm 5 số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 25 và tổng bình phương của chúng bằng 165.
Lời giải:
Gọi số hạng nhỏ nhất là u và công sai là d. Khi đó 5 số hạng đó là a, a + d, a + 2d, a + 3d, a + 4d.
Do tổng 5 số hạng bằng 25 nên ta có
a + (a + d) + (a + 2d) + (a + 3d) + (a + 4d) = 25
⇔ 5a + 10d = 25
⇔ a + 2d = 5
⇔ a = 5 − 2d (1)
Lại có tổng bình phương của chúng bằng 165 nên ta có
a2 + (a + d)2 + (a + 2d)2 + (a + 3d)2 + (a + 4d)2 =165 (2)
Thế (1) vào (2) ta thu được
(5 − 2d)2 + (5−d)2 + 52 + (5 + d)2 + (5 + 2d)2 = 165
⇔ 10d2 + 25.5 = 165
⇔ 10d2 = 40
⇔ d2 = 4
⇔ d = ±2
Với d = −2, ta có a = 9.
Với d = 2, ta có a = 1.
Vậy 5 số cần tìm là 1,3,5,7,9.
Câu 50: Tính (–5).18 + (–5).83 + (–5).(–1).
Lời giải:
(–5).18 + (–5).83 + (–5).(–1)
= –5(18 + 83 – 1)
= – 5 . 100
= –500.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.