Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 92) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 92)
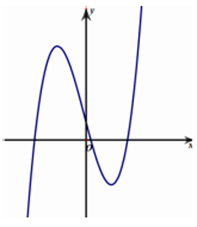
Câu 1: Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d thuộc ℝ) có đồ thị như hình vẽ bên. Tìm số điểm cực trị của hàm số đã cho.
Lời giải:
Từ đồ thị hàm số ta thấy hàm số đã cho có hai điểm cực trị.
Câu 2: Cho x, y là các số thực không âm thỏa mãn: x2 − 2xy + x − 2y ≤ 0. Tìm GTLN của M = x2 − 5y2 + 3x.
Lời giải:
Ta có: x2 − 2xy + x − 2y ≤ 0
⇔ x(x − 2y) + (x − 2y) ≤ 0
⇔ (x − 2y)(x + 1) ≤ 0.
Mà do x, y là các số thực không âm nên x + 1 > 0.
Khi đó x − 2y ≤ 0 ⇔ x ≤ 2y.
Với x, y là các số thực không âm nên ta có:
M = x2 − 5y2 + 3x ≤ (2y)2 − 5y2 + 3.(2y)
= −y2 + 6y = −y2 + 6y − 9 + 9
= −(y − 3)2 + 9 ≤ 9, ∀y
Dấu “=” xảy ra ⇔ y − 3 = 0 ⇔ y = 3.
Vậy GTLN của M là 9 khi y = 3 và x = 2.3 = 6.
Câu 3: Với giá trị nào của m thì ba đường thẳng d1: y = x; d2: y = 4 − 3x và d3: y = mx − 3 đồng quy?
Lời giải:
Xét phương trình hoành độ giao điểm của d1 và d2 là:
x = 4 − 3x ⇔ x = 1 ⇒ y = 1
Suy ra giao điểm của d1 và d2 là điểm M(1; 1).
Để ba đường thẳng trên đồng quy thì M ∈ d3 nên
1 = m.1 − 3 ⇔ m = 4
Vậy m = 4 là giá trị cần tìm của tham số m.
Câu 4: Cho hàm số f (x) đồng biến trên khoảng (a; b). Mệnh đề nào sau đây sai?
A. Hàm số y = f (x + 1) đồng biến trên khoảng (a; b);
B. Hàm số y = −f (x) + 1 nghịch biến trên khoảng (a; b);
C. Hàm số y = f (x) + 1 đồng biến trên khoảng (a; b);
D. Hàm số y = −f (x) − 1 nghịch biến trên khoảng (a; b).
Lời giải:
Ta có: Hàm số đồng biến trên (a; b) ⇔ f ‘(x) ≥ 0 ∀x ∈ (a; b) và bằng 0 tại hữu hạn điểm.
• Đáp án B: y′ = −f ′(x) ⇒ y′ < 0, ∀x ∈ (a; b)
⇒ Hàm số nghịch biến trên (a; b).
Vậy đáp án B đúng.
• Đáp án C: y′ = f ′(x) ⇒ y′ > 0, ∀x ∈ (a; b)
⇒ Hàm số đồng biến trên (a; b).
Vậy đáp án C đúng.
• Đáp án D: y′ = −f ′(x) ⇒ y′ < 0, ∀x ∈ (a; b)
⇒ Hàm số nghịch biến trên (a; b).
Vậy đáp án D đúng.
Chọn đáp án A.
Câu 5: Cho hàm số y = f (x) có đạo hàm trên khoảng (a; b). Mệnh đề nào sau đây sai?
A Nếu f ‘(x) > 0, ∀x ∈ (a; b) thì hàm số y = f (x) đồng biến trên (a; b);
B. Nếu f ‘(x) = 0, ∀x ∈ (a; b) thì hàm số y = f (x) không đổi trên (a; b);
C. Nếu hàm số y = f (x) nghịch biến trên (a; b) thì f ‘(x) ≤ 0 với mọi x ∈ (a; b);
D. Nếu hàm số y = f (x) đồng biến trên (a; b) thì f ‘(x) > 0 với mọi x ∈ (a; b);
Lời giải:
Đáp án đúng là: D
• Nếu f ‘(x) > 0, ∀x ∈ (a; b) thì hàm số y = f (x) đồng biến trên (a; b)
Vậy mệnh đề A là đúng.
• Nếu f ‘(x) = 0, ∀x ∈ (a; b) thì hàm số y = f (x) không đổi trên (a; b)
Vậy mệnh đề B là đúng.
• Nếu hàm số y = f (x) nghịch biến trên (a; b) thì f ‘(x) ≤ 0 với mọi x ∈ (a; b)
Vậy mệnh đề C là đúng.
• Nếu hàm số y = f (x) đồng biến trên (a; b) thì f ‘(x) ≥ 0 với mọi x ∈ (a; b)
Vậy mệnh đề D là sai.
Câu 6: Từ các chữ số 1, 2, 3 có thể lập được bao nhiêu số khác nhau có những chữ số khác nhau.
Lời giải:
• Số có 1 chữ số khác nhau là 3 số: 1; 2; 3.
• Số có 2 chữ số khác nhau là 6 số: 12; 21; 13; 31; 23; 32.
• Số có 3 chữ số khác nhau là 6 số: 123; 132; 213; 231; 312; 321.
Vậy ta có 3 + 6 + 6 = 15 (số).
Câu 7: Có bao nhiêu cách sắp xếp 8 viên bi đỏ khác nhau và 8 viên bi đen khác nhau thành một dãy sao cho hai viên bi cùng màu không được ở cạnh nhau?
Lời giải:
Do hai viên bi cùng màu không được đứng cạnh nhau nên ta có trường hợp sau:
• Trường hợp 1: Các viên bi đỏ ở vị trí lẻ.
Có 8 cách chọn viên bi đỏ ở vị trí 1.
Có 7 cách chọn viên bi đỏ ở vị trí 3.
...
Có 1 cách chọn viên bi đỏ ở vị trí 15.
Suy ra có 8.7.6.5.4.3.2.1 cách xếp viên bi đỏ.
Tương tự có 8.7.6.5.4.3.2.1 cách xếp viên bi đen.
Vậy có (8.7.6.5.4.3.2.1)2 cách xếp.
• Trường hợp 2: Các viên bi đỏ ở vị trí chẵn ta cũng có cách xếp tương tự.
Vậy theo quy tắc cộng ta có: 2.(8.7.6.5.4.3.2.1)2 = 3 251 404 800.
Câu 8: Khẳng định nào sau đây là đúng?
A. Nếu hàm số f (x) đồng biến trên (a; b), hàm số g (x) nghịch biến trên (a; b) thì hàm số f (x) + g (x) đồng biến trên (a; b);
B. Nếu hàm số f (x) đồng biến trên (a; b), hàm số g (x) nghịch biến trên (a; b) và đều nhận giá trị dương trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b);
C. Nếu các hàm số f (x), g (x) đồng biến trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b);
D. Nếu các hàm số f (x), g(x) nghịch biến trên (a; b) và đều nhận giá trị âm trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b).
Lời giải:
Đáp án đúng là: D
• A sai: Vì tổng của hàm đồng biến với hàm nghịch biến không kết luận được điều gì.
• B sai: Để cho khẳng định đúng thì g (x) đồng biến trên (a; b).
• C sai: Hàm số f (x), g (x) phải là các hàm dương trên (a; b) mới thoả mãn.
Chọn đáp án D.
Câu 9: Cho hàm số y = f (x). Khẳng định nào sau đây là đúng?
A. Hàm số y = f (x) đạt cực trị tại x0 thì f ‘(x0) = 0;
B. Nếu hàm số đạt cực trị tại x0 thì hàm số không có đạo hàm tại x0 hoặc f ‘(x0) = 0;
C. Hàm số y = f (x) đạt cực trị tại x0 thì nó không có đạo hàm tại x0;
D. Hàm số y = f (x) đạt cực trị tại x0 thì f ‘‘(x0) > 0 hoặc f ‘‘(x0) < 0.
Lời giải:
Nếu hàm số đạt cực trị tại x0 thì hàm số không có đạo hàm tại x0 hoặc f ‘(x0) = 0
Chọn đáp án B.
Câu 10: Khẳng định nào sau đây là đúng?
A. Nếu hàm số f (x) đồng biến trên (a; b), hàm số g (x) nghịch biến trên (a; b) thì hàm số f (x) + g (x) đồng biến trên (a; b);
B. Nếu hàm số f (x) đồng biến trên (a; b), hàm số g (x) nghịch biến trên (a; b) và đều nhận giá trị dương trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b);
C. Nếu các hàm số f (x), g (x) đồng biến trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b);
D. Nếu các hàm số f (x), g(x) nghịch biến trên (a; b) và đều nhận giá trị âm trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b).
Lời giải:
Đáp án đúng là: D
• A sai: Vì tổng của hàm đồng biến với hàm nghịch biến không kết luận được điều gì.
• B sai: Để cho khẳng định đúng thì g (x) đồng biến trên (a; b).
• C sai: Hàm số f (x), g (x) phải là các hàm dương trên (a; b) mới thoả mãn.
Chọn đáp án D.
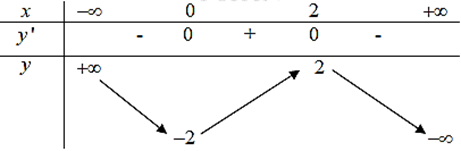
Câu 11: Hàm số y = f (x) có bảng biến thiên sau đây đồng biến trên khoảng nào?
Lời giải:
Dựa vào bảng biến thiên ta thấy, hàm số đồng biến trên khoảng (0; 2).
Câu 12: Nếu hàm số y = f (x) đồng biến trên khoảng (0; 2) thì hàm số y = f (2x) đồng biến trên khoảng nào?
Lời giải:
Ta có hàm số y = f (x) đồng biến trên khoảng (0; 2)
Suy ra f ‘(x) ≥ 0, ∀x ∈ (0; 2)
Xét hàm số y = f (2x) ⇒ y’ = 2f ‘(2x)
Vậy hàm số y = f (2x) đồng biến khi y’ = 2f ‘(2x) ≥ 0 ⇒ f ‘(2x) ≥ 0
Do đó 0 < 2x < 2 ⇔ 0 < x < 1
Vậy hàm số y = f (2x) đồng biến trên khoảng (0; 1).
Câu 13: Giải phương trình 22x + 1 = 32.
Lời giải:
Ta có: 22x + 1 = 32
⇔ 22x + 1 = 25
⇔ 2x + 1 = 5
⇔ 2x = 4
⇔ x = 2
Vậy x = 2 là nghiệm của phương trình đã cho.
Câu 14: Một khối chóp có số mặt bằng 2021 thì có số cạnh bằng bao nhiêu?
Lời giải:
Một khối chóp luôn có một mặt đáy và các mặt bên nên khối chóp có 2021 mặt thì có 2020 mặt bên.
Suy ra mặt đáy có 2020 cạnh, và cũng có 2020 cạnh bên.
Vậy khối chóp đó có tất cả 2020 + 2020 = 4040 (cạnh).
Câu 15: Hình chóp có 2020 cạnh thì có bao nhiêu đỉnh?
Lời giải:
Hình chóp có 2020 cạnh thì có 1011 nhiêu đỉnh.
Câu 16: Người ta làm một cái hộp không có nắp bằng bìa cứng dạng hình lập phương có cạnh 2,5 dm. Tính diện tích bìa cần dùng để làm hộp không tính mép dán.
Lời giải:
Diện tích một mặt của hộp bìa cứng là:
2,5 × 2,5 = 6,25 (dm2)
Diện tích bìa cần dùng để làm hộp không tính mép dán là:
6,25 × 5 = 31,25 (dm2)
Đáp số: 31,25 dm2.
Câu 17: Cho x, y là các số thực không âm thỏa mãn: x2 − 2xy + x − 2y ≤ 0.
Tìm GTLN của M = x2 − 5y2 + 3x.
Lời giải:
Ta có: x2 − 2xy + x − 2y ≤ 0
⇔ x(x − 2y) + (x − 2y) ≤ 0
⇔ (x − 2y)(x + 1) ≤ 0
Mà do x, y là các số thực không âm nên x + 1 > 0
Khi đó x − 2y ≤ 0 ⇔ x ≤ 2y
Với x, y là các số thực không âm nên ta có:
M = x2 − 5y2 + 3x ≤ (2y)2 − 5y2 + 3.(2y)
= −y2 + 6y = −y2 + 6y − 9 + 9
= −(y − 3)2 + 9 ≤ 9, ∀y
Dấu “=” xảy ra ⇔ y − 3 = 0 ⇔ y = 3.
Vậy GTLN của M là 9 khi y = 3 và x = 2.3 = 6.
Câu 18: Cho hàm số f (x) đồng biến trên khoảng (a; b). Mệnh đề nào sau đây sai?
A. Hàm số y = f (x + 1) đồng biến trên khoảng (a; b);
B. Hàm số y = −f (x) + 1 nghịch biến trên khoảng (a; b);
C. Hàm số y = f (x) + 1 đồng biến trên khoảng (a; b);
D. Hàm số y = −f (x) − 1 nghịch biến trên khoảng (a; b).
Lời giải:
Ta có:
Hàm số đồng biến trên (a; b) ⇔ f ‘(x) ≥ 0 ∀x ∈ (a; b) và bằng 0 tại hữu hạn điểm.
+) Đáp án B: y′ = −f ′(x) ⇒ y′ < 0, ∀x ∈ (a; b)
⇒ Hàm số nghịch biến trên (a; b).
Vậy đáp án B đúng.
+) Đáp án C: y′ = f ′(x) ⇒ y′ > 0, ∀x ∈ (a; b)
⇒ Hàm số đồng biến trên (a; b).
Vậy đáp án C đúng.
+) Đáp án D: y′ = −f ′(x) ⇒ y′ < 0, ∀x ∈ (a; b)
⇒ Hàm số nghịch biến trên (a; b).
Vậy đáp án D đúng.
Chọn đáp án A.
Câu 19: Cho hàm số y = f (x) có đạo hàm trên khoảng (a; b). Mệnh đề nào sau đây sai?
A Nếu f ‘(x) > 0, ∀x ∈ (a; b) thì hàm số y = f (x) đồng biến trên (a; b);
B. Nếu f ‘(x) = 0, ∀x ∈ (a; b) thì hàm số y = f (x) không đổi trên (a; b);
C. Nếu hàm số y = f (x) nghịch biến trên (a; b) thì f ‘(x) ≤ 0 với mọi x ∈ (a; b);
D. Nếu hàm số y = f (x) đồng biến trên (a; b) thì f ‘(x) > 0 với mọi x ∈ (a; b);
Lời giải:
+) Nếu f ‘(x) > 0, ∀x ∈ (a; b) thì hàm số y = f (x) đồng biến trên (a; b)
Vậy mệnh đề A là đúng.
+) Nếu f ‘(x) = 0, ∀x ∈ (a; b) thì hàm số y = f (x) không đổi trên (a; b)
Vậy mệnh đề B là đúng.
+) Nếu hàm số y = f (x) nghịch biến trên (a; b) thì f ‘(x) ≤ 0 với mọi x ∈ (a; b)
Vậy mệnh đề C là đúng.
+) Nếu hàm số y = f (x) đồng biến trên (a; b) thì f ‘(x) ≥ 0 với mọi x ∈ (a; b)
Vậy mệnh đề D là sai.
Chọn đáp án D.
Câu 20: Tìm số đo mỗi góc của ngũ giác đều.
Lời giải:
Tổng số đo các góc của ngũ giác là:
180° . (5 − 2) = 540°
Vì ngũ giác đều có 5 góc bằng nhau nên số đo mỗi góc là:
540° : 5 = 108°
Vậy số đo mỗi góc của ngũ giác đều là: 108°.
Câu 21: Đồ thị hàm số nào sau đây không nhận trục Oy làm trục đối xứng?
A. y1 = xsin2 x;
B. y2 = sin2 x;
C. y3 = cos x;
D. y4 = xtan 2x.
Lời giải:
• Xét hàm số y2 = sin2 x có sin x = −sin (−x) ⇒ sin2 x = sin2 (−x)
Do đó hàm y2 là hàm chẵn nên nó nhận trục Oy làm trục đối xứng.
• Xét hàm số y3 = cos x có cos x = cos (−x)
Do đó hàm y3 là hàm chẵn nên nó nhận trục Oy làm trục đối xứng.
• Xét hàm số y4 = xtan 2x có (−x)tan (−2x) = xtan 2x
Do đó hàm y4 là hàm chẵn nên nó nhận trục Oy làm trục đối xứng.
• Xét hàm số y1 = xsin2 x có (−x)sin2 (−x) = − xsin2 x
Do đó hàm y1 là hàm lẻ nên không nhận tục Oy làm trục đối xứng.
Chọn đáp án A.
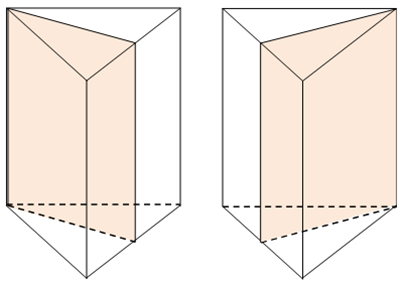
Câu 22: Hình lăng trụ tam giác đều có tất cả các cạnh bằng nhau có bao nhiêu mặt phẳng đối xứng?
Lời giải:
Hình lăng trụ tam giác đều có tất cả các cạnh bằng nhau có 4 mặt phẳng đối xứng như hình vẽ sau.
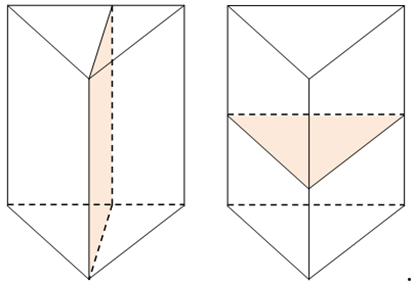
Câu 23: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = (3 − 5sin x)2018 là M và m. Khi đó giá trị M + m là:
Lời giải:
Ta có: −1 ≤ sin x ≤ 1 ⇔ −5 ≤ −5sin x ≤ 5
⇔ −2 ≤ 3 − 5sin x ≤ 8
Suy ra 0 ≤ (3 − 5sin x)2018 ≤ 82018 = 26054
Vậy M = 26054 và m = 0.
Do đó M + m = 26054 + 0 = 26054.
Câu 24: Cho đường tròn (O; R). Có bao nhiêu phép vị tự biến (O; R) thành chính nó?
Lời giải:
Gọi O là tâm đường tròn
Để qua phép vị tự V biến đường tròn (C) thành chính nó thì sẽ biến tâm đường tròn O thành chính nó.
Suy ra, tâm vị tự chính là tâm đường tròn.
Vì R' = R nên k = 1 hoặc k = −1
Vậy có hai phép vị tự thỏa mãn: Phép vị tự tâm O tỉ số 1 và phép vị tự tâm O tỉ số −1.
Câu 25: Cho hàm số y = (m − 1)x + m. Xác định giá trị của m để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2.
Lời giải:
Để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2 thì:
y = (m − 1).0 + m = 2
⇔ m = 2.
Vậy m = 2 là giá trị của m thỏa mãn.
Câu 26: Cho y = 2x + m + 1. Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2.
Lời giải:
Để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2 thì:
y = 2.0 + m + 1 = 2
⇔ m + 1 = 2
⇔ m = 1.
Vậy m = 1 là giá trị của m thỏa mãn.
Câu 27: Tìm tập xác định D của hàm số y = ln(x – 1).
A. D = (−∞; −1);
B. D = (−1; + ∞);
C. D = (−∞; 1);
D. D = (1; +∞).
Lời giải:
Đáp án đúng là: C
Điều kiện xác định: 1 – x > 0 ⇔ x < 1
Vậy tập xác định của hàm số là: D = (−∞; 1).
Câu 28: Tìm tập xác định D của hàm số y = ln(x – 3).
A. D = (3; +∞);
B. D = (−∞; + ∞);
C. D = (0; +∞);
D. D = (e; +∞).
Lời giải:
Đáp án đúng là: A.
Điều kiện xác định: x – 3 > 0 ⇔ x > 3
Vậy tập xác định của hàm số là: D = (3; +∞).
Câu 29: Cho tứ giác ABCD như hình dưới đây: Điểm E là trung điểm của đoạn thẳng AB. Điểm F là trung điểm của đoạn thẳng BC. Điểm G là trung điểm của đoạn thẳng DC. Điểm H là trung điểm của đoạn thẳng AD. Hỏi tứ giác EFGH là hình gì? Chứng minh điều đó.
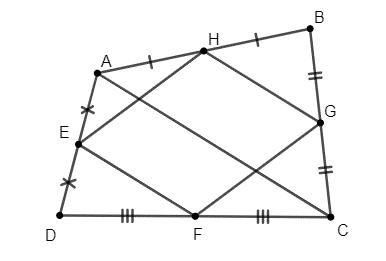
Lời giải:
Ta có:
• EF là đường trung bình của tam giác ABC, nên ta suy ra được EF // AC (1)
• HG là đường trung bình của tam giác ADC, nên ta suy ra được HG // AC (2)
Từ (1) và (2) suy ra EF // HC
Tương tự ta có:
• FG là đường trung bình của tam giác BDC, nên FG // BD (3)
• EH là đường trung bình của tam giác BDA, nên EH // BD (4)
Từ (3) và (4) ta có FG // EH
Xét tứ giác EFGH ta có: EF // HG và FG // EH.
Do đó suy ra tứ giác EFGH là hình bình hành.
Câu 30: Hình bên là đồ thị của ba hàm số y = ax, y = bx, y = cx (0 < a, b, c ≠ 1) được vẽ trên cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?
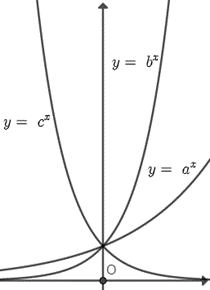
A. a > b > c;
B. c > b > a;
C. a > c > b;
D. b > a > c.
Lời giải:
Đáp án đúng là: D.
Đồ thị hàm số y = cx có dạng đi xuống nên 0 < c < 1.
Đồ thị hàm số y = bx; y = ax có dạng đi lên và đồ thị y = bx nằm phía trên đồ thị hàm số y = ax nên b > a > 1.
Do đó ta có b > a > c.
Câu 31: Cho hàm số y = log2 x. Khẳng định nào sau đây sai?
A. Đồ thị hàm số nhận trục tung làm tiệm cận đứng.
B. Đồ thị hàm số cắt trục hoành tại điểm A(1; 0).
C. Đồ thị hàm số luôn nằm trên phía trục hoành.
D. Hàm số đồng biến trên khoảng (0; +∞).
Lời giải:
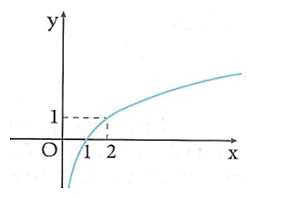
Hàm số y = log2 x có đồ thị như hình trên.
Từ đồ thị hàm số ta thấy các khẳng định A, B, D là đúng, khẳng định C sai.
Câu 32: Một trong các bạn A, B, C và D làm vỡ kính cửa sổ. Khi được hỏi, họ trả lời như sau:
A: “C làm vỡ”.
B: “Không phải tôi”.
C: “D làm vỡ”.
D: “C đã nói dối”.
Nếu có đúng một người nói thật thì ai đã làm vỡ cửa số.
Lời giải:
• Trường hợp 1: A, B nói thật ⇒ D nói dối ⇒ C nói thật.
⇒ Loại.
• Trường hợp 2: C nói thật ⇒ D làm vỡ
C nói thật ⇒ B nói dối ⇒ B làm vỡ.
⇒ Loại.
• Trường hợp 3: D nói thật ⇒ B nói dối
⇒ B làm vỡ.
Vậy B là người là vỡ.
Câu 33: Số đo mỗi góc của ngũ giác đều là bao nhiêu?
Lời giải:
Tổng số đo các góc của ngũ giác là: 180º . (5 − 2) = 540º .
Vì ngũ giác đều có 5 góc bằng nhau nên số đo mỗi góc là: 540º : 5 = 108º.
Câu 34: Trong các hình sau: hình chữ nhật, hình lục giác đều, hình tam giác. Hình nào không có tâm đối xứng?
Lời giải:
Tâm đối xứng của hình chữ nhật, hình vuông, hình lục giác đều được biểu diễn dưới hình sau.
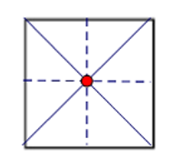
Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo.
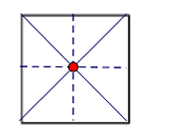
Tâm đối xứng của hình vuông là giao điểm của ba đường chéo.
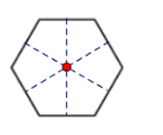
Tâm đối xứng của hình lục giác đều là giao điểm của ba đường chéo chính.
Vậy hình không có tâm đối xứng là hình tam giác.
Câu 35: Tìm m để phương trình: cos2x = m – 1 có nghiệm.
Lời giải:
Ta có: cosx ∈ [−1; 1]
Để phương trình có nghiệm thì:
− 1 ≤ m − 1 ≤ 1 suy ra 0 ≤ m ≤ 2
Vậy m ∈ [0; 2].
Câu 36: Tính đạo hàm của hàm số sin2 x.
Lời giải:
(sin2 x)’ = 2sin x.(sin x)’ = 2sin x cos x = sin 2x.
Vậy đạo hàm của hàm số sin2 x là sin 2x.
Câu 37: Có 6 quả cầu xanh đánh số từ 1 đến 6, 5 quả cầu đỏ đánh số từ 1 đến 5 và 7 quả màu vàng đánh số từ 1 đến 7. Hỏi có bao nhiêu cách lấy ra 3 quả cầu vừa khác màu vừa khác số?
Lời giải:
Để lấy ra ba quả cầu vừa khác màu vừa khác số ta phải thực hiện qua ba giai đoạn:
• Chọn một quả cầu đỏ
• Chọn một quả cầu xanh
• Chọn một quả cầu vàng
Chọn quả cầu đỏ có 5 cách chọn
Chọn quả cầu xanh có 5 cách chọn (trừ quả cầu được đánh số trùng với quả cầu đỏ)
Chọn quả cầu vàng có 5 cách chọn (trừ hai quả cầu được đánh số trùng với quả cầu đỏ và quả cầu xanh)
Theo quy tắc nhân ta được 5. 5. 5 = 125 cách lấy ra ba quả cầu vừa khác màu vừa khác số
Vậy có 125 cách lấy ra ba quả cầu vừa khác màu vừa khác số.
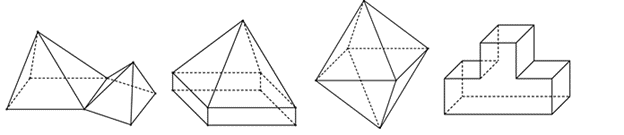
Câu 38: Có bao nhiêu hình đa diện trong các hình dưới đây?
Lời giải:
Quan sát hình vẽ ta thấy có hình 1 không phải hình đa diện.
Ba hình còn lại đều là hình đa diện.
Vậy có 3 hình đa diện.
Câu 39: Gọi S là tập hợp các số tự nhiên có hai chữ số. Trong các số: 7; 15; 106; 99, số nào thuộc và số nào không thuộc tập S? Dùng kí hiệu để trả lời.
Lời giải:
Vì S là tập hợp các số tự nhiên có hai chữ số nên tập S là tập hợp các số tự nhiên lớn hơn 9 và nhỏ hơn 100.
Do đó: S = {x | x là số tự nhiên và 9 < x < 100}.
Nhận thấy: 15; 99 là phần tử của S, 7; 106 không là phần tử của S
Vậy 7 ∉ S; 15 ∈ S; 106 ∉ S; 99 ∈ S.
Câu 40: Trong không gian Oxyz, mặt phẳng (Oxz) có phương trình là
A. z = 0.
B. x + y + z = 0.
C. y = 0.
D. x = 0.
Lời giải:
Đáp án đúng là: C
Mặt phẳng (Oxz) có phương trình là y = 0.
Câu 41: Trên một kệ sách có 5 quyển sách Toán, 4 quyển sách Lí, 3 quyển sách Văn. Các quyển sách đều khác nhau. Hỏi có bao nhiêu cách sắp xếp các quyển sách trên:
a) Một cách tuỳ ý?
b) Theo từng môn và sách Toán nằm ở giữa?
Lời giải:
a) Có tất cả 5 + 4 + 3 = 12 quyển sách.
Cách sắp xếp các quyển sách một cách tùy ý là: 12! (cách)
b) Chọn vị trí ở giữa cho 5 quyển sách Toán nên có số cách là 5! (cách)
Chọn vị trí đầu cho sách lý, có số cách là 4! (cách)
Chọn vị trí cuối cho sách văn, có số cách là 3! (cách)
Hoán đổi vị trí đầu và vị trí cuối nên thêm 2! (cách)
Vậy số cách sắp xếp các quyển sách trên theo từng môn và sách Toán nằm ở giữa là:
4!.5!.3!.2! = 34560 (cách)
Câu 42: Trên một kệ sách có 5 quyển sách Toán, 4 quyển sách Lí, 3 quyển sách Văn. Các quyển sách đều khác nhau. Hỏi có bao nhiêu cách sắp xếp các quyển sách trên theo từng môn?
Lời giải:
Ta phân nhóm mỗi loại sách theo từng môn, xếp 3 nhóm có 3!3! (cách).
Trong mỗi nhóm, ta xếp từng loại sách:
+) Xếp sách Toán có 5! (cách).
+) Xếp sách Lí có 4! (cách).
+) Xếp sách Văn có 3! (cách).
Như vậy có 3!.5!.4!.3!=103680 (cách)
Câu 43: Cho a, b, c là ba số thực dương và khác 1. Đồ thị các hàm số y = ax, y = logbx, y = logcx được cho trong hình dưới đây:
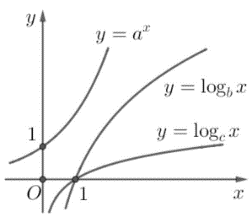
Mệnh đề nào dưới đây đúng?
A. a < b < c.
B. c < b < a.
C. b < c < a.
D. b < a < c.
Lời giải:
Đáp án đúng là: D.
Kẻ đường thẳng x = 1 cắt đồ thị hàm số y = ax tại điểm có tung độ a; kẻ đường thẳng y = 1 cắt đồ thị hàm số y = logbx, y = logcx lần lượt tại các điểm có hoành độ b, c.
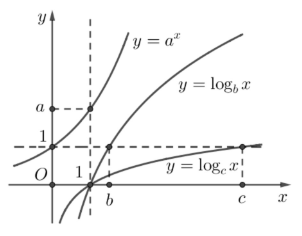
Quan sát hình vẽ suy ra c > a > b.
Câu 44: Với a là số thực dương tùy ý, tìm giá trị của log3(3a).
Lời giải:
Ta có: log3(3a) = log33 + log3a = 1 + log3a.
Câu 45: Một đĩa gốm cổ cần được phục hồi. Hãy xác định tâm và bán kính của đĩa. Lấy 2 điểm A, B thuộc đường tròn lớn và 2 điểm C, D thuộc đường tròn nhỏ. Xác định giao điểm 2 đường trung trực của AB và CD.

Lời giải:
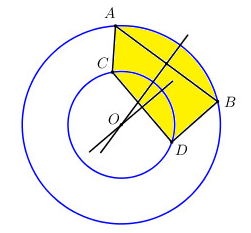
Dễ thấy đĩa có 2 đường tròn, đường tròn lớn và đường tròn nhỏ là hai đường tròn đồng tâm.
Lấy hai điểm A, B trên đường tròn lớn và 2 điểm C, D trên đường tròn nhỏ.
Dựng d là đường trung trực của AB, d’ là trung trực của CD. Gọi O = d ∩ d′.
Ta có:
Do O thuộc trung trực của AB nên OA = OB.
Do O thuộc trung trực của CD nên OC = OD.
Vậy khi đó O chính là tâm của đĩa.
Câu 46: Phân tích đa thức sau thành nhân tử: x2 – 6x + 2(x – 6).
Lời giải:
Ta có: x2 – 6x + 2(x – 6) = x(x – 6) + 2(x – 6) = (x + 2)(x – 6).
Câu 47: Một người đem gửi tiền tiết kiệm vào một ngân hàng với lãi suất 1% một tháng. Biết rằng cứ sau mỗi quý (3 tháng) thì lãi sẽ được cộng dồn vào vốn gốc. Hỏi sau tối thiểu bao nhiêu năm thì người đó nhận lại được số tiền bao gồm cả vốn lẫn lãi gấp ba lần số tiền ban đầu?
Lời giải:
Gọi T là số tiền sau khi lãi được cộng dồn vào gốc, P là số tiền ban đầu.
Gọi n là số quý gửi tiết kiệm (quý).
Cứ sau mỗi quý thì lãi sẽ được cộng dồn vào vốn gốc ⇒ Kì hạn là 1 quý (3 tháng)
⇒ Lãi suất là: 1%.3 = 3% (1 quý)
Để nhận được số tiền gấp 3 lần ban đầu thì T = 3P ⇔ P(1 + 3%)n = 3P
⇔ (1 + 3%)n = 3 ⇔ n = log1,033 = 37,16.
Mà mỗi năm có 4 quý ⇒ Cần tối thiếu số năm là: 37,16 : 4 = 9,29 (năm)
⇒ Làm tròn lên 10 năm.
Câu 48: Có bao nhiêu cặp số nguyên (x; y) thỏa mãn 0 ≤ x ≤ 2020 và log3(3x + 3) + x = 2y + 9y?
Lời giải:
ĐKXĐ: 3x + 3 > 0 ⇔ x > −1.
Ta có: log3(3x + 3) + x = 2y + 9y
⇔ log3[3(x + 1)] + x = 2y + 32y
⇔ log33 + log3(x + 1) + x = 2y + 32y
⇔ log3(x + 1) + x + 1 = 2y + 32y
⇔log3(x + 1) + 3log3(x + 1) = 2y + 32y
Xét hàm đặc trưng f(t) = t + 3t ta có f ′(t) = 1 + 3tln3 > 0.
⇒ Hàm số y = f(t) đồng biến trên ℝ, do đó ta có log3(x + 1) = 2y
⇔ x + 1 = 32y.
Theo bài ra ta có: 0 ≤ x ≤ 2020
⇔ 0 ≤ 32y – 1 ≤ 2020
⇔ 1 ≤ 32y ≤ 2020
⇔ 0 ≤ 2y ≤ log32020 ≈ 6,9
Mà y ∈ Z ⇒ y ∈ {0; 1; 2; 3}.
Ứng với mỗi giá trị của y cho 1 giá trị x tương ứng.
Vậy có 4 cặp số nguyên (x;y) thỏa mãn yêu cầu bài toán.
Câu 49: Bạn An ra nhà sách và mang theo một số tiền vừa đủ để mua 10 quyển tập và 6 cây bút. Nhưng khi ra đến nơi, giá một quyển tập mà bạn An định mua đã tăng lên 500 đồng một quyển tập, còn giá một cây bút thì giảm 1000 đồng một cây so với dự định. Vậy để mua 10 quyển tập và 6 cây bút như trên thì bạn An còn thừa hay thiếu số tiền là bao nhiêu?
Lời giải:
Gọi x (đồng), y (đồng) lần lượt là giá 1 quyển tập và 1 cây cây bút dự định (x > 0,
y > 1000)
Số tiền An mang theo: S1 = 10x + 6y (đồng)
Số tiền An mua trong thực tế: S2 = 10(x + 500) + 6(y – 1000) (đồng)
Ta có S2 = 10x + 5000 + 6y – 6000 = 10x + 6y – 1000 = S1 – 1000
Vậy để mua 10 quyển tập, 6 cây bút như trên thì bạn An còn thiếu số tiền là 1000 đồng.
Câu 50: Một bồn nước inox có dạng một hình trụ với chiều cao 1,75m và diện tích đáy là 0,32m2. Hỏi bồn nước này đựng đầy được bao nhiêu mét khối nước?
Lời giải:
Thể tích bồn nước là:
V = S.h = 0,32.1,75 = 0,56 (m3)
Vậy bồn nước đựng đầy được 0,56 mét khối nước.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.