Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 40) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 40)
Câu 1: Tìm số tự nhiên nhỏ nhất có ba chữ số khi chia cho 18; 30; 45 có số dư lần lượt là: 8; 20; 35
Lời giải:
Gọi số cần tìm là a, ta có:
• a = 18.n + 8 ⇔ a + 10 = (18.n + 18) ⋮ 18;
• a = 30.m + 20 ⇔ a + 10 = (30.m + 30) ⋮ 30;
• a = 45.k + 35 ⇔ a + 10 = (45.k + 45) ⋮ 45.
(với n, m, k ∈ ℕ)
Do đó A + 10 là bội chung của 18; 30; 45.
Mà BCNN(18, 30, 45) = 90 nên BC(18, 30, 45) = 90.x với x ∈ ℕ*
Do đó ta có: A + 10 = 90.x.
Vì A là số có 3 chữ số nhỏ nhất nên 1 < x < 3
Với x = 2 ⇔ A + 10 = 180
Vậy A = 170.
Câu 2: Hỗn số 314 được viết dưới dạng số thập phân là bao nhiêu?
Lời giải:
Hỗn số 314 được viết dưới dạng số thập phân là:
134= 6,25.
Lời giải:
Gọi a (học sinh) là số học sinh khối 6.
Ta có:
• a : 8 dư 3 ⇔ (a - 3) ⋮ 8
• a : 11 dư 1 ⇔ (a - 1) ⋮ 11
Ta có: (a - 3) ∈ B(8) và (a - 1) ∈ B(11)
Mà 100 < a < 200
Khi đó:
• (a -3) ∈ {104; 112; 120; ... ; 152; ... ; 192} và
• (a -1) ∈ {110; 121; ...154; ... 198}
Do đó a = 155
Vậy số học sinh khối 6 của trường đó là 55 học sinh.
Lời giải:
Gọi x là số học sinh khối 6 (x ∈ ℕ, đơn vị: học sinh)
Ta có: x ⋮ 8; x ⋮ 10; x ⋮ 15; x ⋮ 20
x ∈ BC(8, 10, 15, 20)
8 = 23 ; 10 = 2.5; 15 = 3.5; 20 = 22.5
BCNN(8, 10, 15, 20) = 23.3.5 = 120
x ∈ B(120) = {0; 120; 240; 480; ...}
mà 100 < x < 200 nên x = 120
Vậy số học sinh khối 6 là 120 học sinh.
Lời giải:
Nếu làm xong trong 14 ngày thì cần số người là:
14 × 3 = 42 (người)
Vậy làm xong trong 7 ngày thì cần số người là:
42 : 7 = 6 (người)
Đáp số: 6 người.
Lời giải:
1 thùng chứa:
27 : 3 = 9 (lít)
Có tất cả số thùng là:
12 + 5 = 17 (thùng)
Có tất cả số lít mật ong là:
9 × 17 = 153 (lít)
Đáp số: 153 lít mật ong
Lời giải:
Để ăn hết số gạo đó trong 1 ngày cần số em là:
120 × 20 = 2400 (em)
Số gạo còn ăn được trong số ngày nữa là:
20 - 4 = 16 (ngày)
Số em đến thêm là:
(2400 : 16) - 120 = 30 (em)
Đáp số: 30 em.
Lời giải:
Gọi ¯a1a2a3a4a5 là các số tự nhiên cần tìm
Xét a1 = 5
Chọn ¯a1a2a3a4a5: A46cách
⇔ 360 số
Xét a1 ≠ 5 ⇔ a1 có 5 cách
Đặt chữ số 5 có 4 cách
Chọn 3 vị trí còn lại A35
⇔ Có 5.4.A35=1200 số
Vậy có 1200 + 360 = 1560 số
Lời giải:
Vì ABCD là hình bình hành nên AB = CD = 35 cm.
Diện tích hình bình hành đó là:
35 × 42 = 1470 (cm2)
Độ dài đường cao AK là:
1470 : 30 = 49 (cm)
Đáp số: 49 cm.
Lời giải:
Cả 3 đợt cửa hàng đã nhập về:
150 × 3 = 450 (kg)
Đợt 2 cửa hàng nhập về:
170 + 40 = 210 (kg)
Đợt 3 cửa hàng nhập về:
450 - 170 - 210 = 70 (kg)
Đáp số: 70 kg.
Lời giải:
Một bạn lớp 5A trồng 3 cây thì thừa 2 cây.
Một bạn 5B trồng 4 cây thì thiếu 38 cây, cũng như 1 bạn 5A trồng 4 cây thì thiếu:
38 + 5 = 43 (cây)
Số cây đủ cho một bạn trồng 4 cây nhiều hơn số cây đủ cho một bạn trồng 3 cây là:
2 + 43 = 45 (cây)
Một bạn trồng 4 cây nhiều hơn một bạn trồng 3 cây số cây là:
4 - 3 = 1 (cây)
Số học sinh lớp 5A (hoặc lớp 5B) là:
45 : 1 = 45 (học sinh)
Lớp 5A trồng được số cây là:
45 × 3 + 2 = 137 (cây)
Lớp 5B trồng được số cây là:
45 × 4 - 38 = 142 (cây)
Đáp số: Lớp 5A: 137 cây;
Lớp 5B: 142 cây.
Lời giải:
Số có 4 chữ số khác nhau và tổng các chữ số bằng 9 là: 6210; 6120.
Tích các chữ số là: 6 × 2 × 1 × 0 = 0; 6 × 1 × 2 × 0 = 0.
Đáp số: 0.
Câu 13: Tìm hiệu của số lớn nhất có bốn chữ số khác nhau và số bé nhất có bốn chữ số khác nhau.
Lời giải:
Số lớn nhất có 4 chữ số khác nhau là: 9876
Số bé nhất có 4 chữ số khác nhau là: 1023
Hiệu của chúng là: 9876 - 1023 = 8853
Đáp số: 8853.
Lời giải:
Số chia hết cho cả 8 và 6 là:
6 × 8 = 48
Hiệu của 8 và 6 là:
8 - 6 = 2
Số cần tìm là:
48 : 2 × 4 = 96
Đáp số: 96.
Lời giải:
Chiều cao miếng đất là:
57 : 3 = 28,5 (m)
Diện tích miếng đất là:
25 × 28,5 = 712,5 (m2)
Đáp số: 712,5 m2.
Lời giải:
Chiều cao miếng đất là:
51 : 3 = 17 (m)
Diện tích miếng đất là:
25 × 17 = 425 (m2)
Đáp số: 425 m2.
Lời giải:
Số khăn mỗi ngày chị thứ nhất dệt ít hơn chị thứ hai là:
56 - 48 = 8 (cái)
Sau khi dệt một số ngày thì số khăn chị thứ nhất dệt ít hơn chị thứ hai là:
48 : 8 = 6 (cái)
Số khăn mỗi chị dệt được là:
48 × 6 + 62 = 350 (cái)
Đáp số: 350 cái
Câu 18: Tính: 1 + 2 + 3 + ... + 99 + 100
Lời giải:
1 + 2 + 3 + ... + 99 + 100
= (1 + 99) + (2 + 98) + (3 + 97) + ... + 100
= 100 + 100 + 100 + ... + 100 (50 số 100)
= 100 × 50
= 5000
Lời giải:
Gọi x là ước chung của ba số
144 = 24.32
192 = 26.3
240 = 24.3.5
ƯCLN(144, 192, 240) = 24.3
ƯC(144, 192, 240) ∈ {0; 48; 96; 144; ...}
mà x là số tự nhiên có hai chữ số nên x ∈ {48; 96}.
Vậy x ∈ {48; 96}.
Câu 20: Tìm số tự nhiên x biết 144 ⋮ x, 192 ⋮ x và x > 20.
Lời giải:
Gọi x là ước chung của hai số
Ta có 144 = 24.32; 192 = 26.3.
Suy ra ƯCLN(144, 192) = 24.3
Do đó ƯC(144, 192) ∈ {0; 48; 96; 144; ...}
Mà x là số tự nhiên có hai chữ số nên x ∈ {48; 96}
Vậy x ∈ {48; 96}.
Lời giải:
Gọi x là số nhỏ nhất cần tìm (x > 1950)
Ta có x ⋮ 5 dư 4; x ⋮ 4 dư 3; x ⋮ 3
⇒{(x−4) ⋮ 5(x−3) ⋮ 4x ⋮ 3⇒{(x−4+25) ⋮ 5(x−3+24) ⋮ 4x ⋮ 3⇒{(x+21) ⋮ 5(x+21) ⋮ 4(x+21) ⋮ 3
x + 21 là BC(3, 4, 5)
Mà x + 21 là số nhỏ nhất
⇔ (x + 21) là BCNN(3, 4, 5) ∈ {0; 60; 120; 180; ... ; 1920; 1980; ... }
Mà x > 1950 ⇔ (x + 21) > 1971
⇔ x + 21 = 1980
⇔ x = 1961.
Vậy số nhỏ nhất thoả mãn các điều kiện bài toán là 1961.
Câu 22: Tính nhanh 1 + 3 + 9 + 27 + 81 + 243 + 729 + 2 187 + 6 561 + 19 683 + 59 049
Lời giải:
Ta có: 1 + 3 + 9 + 27 + 81 + 243 + 729 + 2 187 + 6 561 + 19 683 + 59 049
= (1 + 59 049) + (3 + 2 187) + (9 + 6 561) + (27 + 243) + (81 + 729) + 19 683
= 59 050 + 2 190 + 6 570 + 270 + 810 + 19 683
= 59 050 + (2190 + 810) + 6570 + 270 + 19 683
= 59 050 + 3 000 + 6 570 + 270 + 19 683
= 59 050 + (3 000 + 6 570) + 270 + 19 683
= 59 050 + 9 570 + 270 + 19 683
= 68 620 + 270 + 19 683
= 68 890 + 19 683
= 88 583.
Câu 23: Tìm số tự nhiên x biết 280 ⋮ x, 700 ⋮ x, 420 ⋮ x và 40 < x < 100.
Lời giải:
Do 280 ⋮ x; 700 ⋮ x; 420 ⋮ x
⇔ x ∈ ƯC(280, 700, 420)
280 = 23.5.7
700 = 22.52.7
420 = 22.3.5.7
Mà ƯCLN(280, 700, 420) = 22.5.7 = 140
x ∈ ƯC(140) = {1; 2; 4; 5; 7; 10; 14; 20; 28; 35; 70; 140}
Mà 40 < x < 100
⇔ x = 70
Vậy x = 70
Lời giải:
Gọi khoảng thời gian để 2 xe cùng rời bến lần 2 là a (phút); a ∈ ℕ*
Theo bài ra, ta có: a ⋮ 10; a ⋮ 12 và a nhỏ nhất nên a = BCNN(10, 12).
Ta có: 10 = 2.5; 12 = 22.3
Suy ra BCNN(10, 12) = 22.3.5 = 60.
Hay A = 60
Do đó khoảng thời gian để 2 xe cùng cập bến lần 2 là 60 phút tức 1 giờ
Vậy 2 xe cùng cập bến lần tiếp theo lúc: 6 + 1 = 7 (giờ).
Lời giải:
Số phút tiếp theo sớm nhất để một xe buýt tuyến 26 và một xe buýt tuyến 50 cùng đến sân vận động Quốc gia Mỹ Đình là bội chung nhỏ nhất của 10 và 15.
Mà BCNN(10, 15) = 30.
Khi đó sau ít nhất 30 phút thì xe buýt tuyến 26 và một xe buýt tuyến 50 cùng đến sân vận động Quốc gia Mỹ Đình.
Vậy thời điểm tiếp theo là lúc 3 giờ 30 phút chiều thì một xe buýt tuyến 26 và một tuyến xe buýt 50 cùng đến sân vận động Quốc gia Mỹ Đình.
Lời giải:
Ta có sơ đồ:
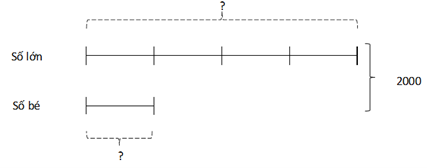
Tổng chúng là : 1975 + 79 - 54 = 2000
Tổng số phần bằng nhau : 1 + 4 = 5 (phần)
Số bé là : 2000 : 5 = 400
Số lớn là : 2000 - 400 = 1600
Đáp số: Số bé: 400;
Số lớn: 1600.
Lời giải:
Chiều dài gấp rưỡi chiều rộng nghĩa là chiều dài bằng 32 chiều rộng.
Nếu chiều rộng thêm 20 m và chiều dài thêm 40 m thì chiều dài vẫn gấp đôi chiều rộng.
Như thế chiều dài tăng thêm:
40 - 15 = 25 (m)
25 m ứng với:
42−32=12 (chiều rộng khi đã thêm)
Chiều rộng khi đã thêm 20 m là:
25 × 2 = 50 (m)
Chiều rộng ban đầu là:
50 - 20 = 30 (m)
Chiều dài ban đầu là:
30 × 2 = 60 (m)
Diện tích thửa ruộng là:
60 × 30 = 1800 (m2)
Đáp số: 1800 m2.
Câu 28: Thực hiện phép tính (x + 2y + z)(x + 2y – z).
Lời giải:
(x + 2y + z)(x + 2y – z)
= (x + 2y)2 – z2
= x2 + 4y + 4y2 – z2.
Câu 29: Điền vào chỗ trống cho thích hợp:
a) x2 + 4x + 4 = …
b) (x + 2).(x2 – 2x + 4) = …
c) x3 – 6x2 + 12x – 8 = …
d) (x + 5).(x – 5) = …
Lời giải:
a) x2 + 4x + 4 = (x + 2)2
b) (x + 2).(x2 – 2x + 4) = x3 + 8
c) x3 – 6x2 + 12x – 8 = (x – 2)3
d) (x + 5).(x – 5) = x2 – 25
Câu 30: Điền vào chỗ trống cho thích hợp
a) x2 + 4x + 4 = …
b) (x – 3)(x2 + 3x + 9) = …
c) x2 – 1 = …
d) 36x2 + 36x + 9 = …
Lời giải:
a) x2 + 4x + 4 = (x + 2)2
b) (x - 3)(x2 + 3x + 9) = x3 – 27
c) x2 – 1 = (x – 1)(x + 1)
d) 36x2 + 36x + 9 = 9(2x + 1)2
Câu 31: So sánh A và B biết: A = (2 + 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1) và B = 232.
Lời giải:
A = (2 – 1)(2 + 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1) (nhân với 2 – 1 =1. Giá trị không thay đổi)
A = (22 – 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1)
A = (24 – 1)(24 + 1)(28 + 1)(216 + 1)
A = (28 – 1)(28 + 1)(216 + 1)
A = (216 – 1)(216 + 1)
A = 232 – 1 < 232 = B
Vậy A < B.
Câu 32: Tỉ số phần trăm của 28 và 80 là bao nhiêu?
Lời giải:
Tỉ số phần trăm của 28 và 80 là :
(28 : 80) × 100 % = 35 %
Câu 33: Cho số tự nhiên, mệnh đề đúng là:
A. ∀ n, n + 1 là số chẵn;
B. ∀ n, n(n + 1) là số lẻ;
C. ∃ n, n(n + 1)(n + 2) là số lẻ;
D. ∀ n, n(n + 1)(n + 2) là số chia hết cho 6.
Lời giải:
Đáp án đúng là: D
A sai vì nếu n là số lẻ thì n + 1 là số chẵn
B sai vì hai số tự nhiên liên tiếp có một số chẵn nên tích của hai số tự nhiên liên tiếp luôn là số chẵn
C sai vì ba số tự nhiên liên tiếp có ít nhất 1 số chẵn nên tích của ba số tự nhiên liên tiếp luôn là số chẵn
D đúng vì tích của 3 số tự nhiên liên tiếp luôn chia hết cho 2 và 3 nên chia hết cho 6
Câu 34: Cho n là số tự nhiên, mệnh đề nào sau đây đúng?
A. ∀ n, n(n + 1) là số chính phương;
B. ∀ n, n(n + 1) là số lẻ;
C. ∃ n, n(n + 1)(n + 2) là số lẻ;
D. ∀ n, n(n + 1)(n + 2) là số chia hết cho 6.
Lời giải:
Đáp án đúng là: D
∀ n ∈ ℕ, n(n + 1)(n + 2) là tích của 3 số tự nhiên liên tiếp, trong đó, luôn có một số chia hết cho 2 và một số chia hết cho 3 nên nó chia hết cho 2.3 = 6.
Lời giải:
Nếu đổ đầy số can 10 lít bằng với số can 6 lít thì còn thiếu:
10 × 5 - 2 = 48 (lít)
Thiếu 48 lít này do mỗi can 6 lít ít hơn:
10 - 6 = 4 (lít)
Số can 6 lít: 48 : 4 = 12 (can)
Số lít dầu: 6 × 12 = 72 (lít)
Lời giải:
Giả sử bạn Dung mua số quyển vở gấp đôi và số bút chì cũng gấp đôi thì giá tiền là:
57 000 × 2 = 114 000 (đồng)
Vậy số bút chì bạn Dung mua nhiều hơn số bút chì bạn Công mua là:
12 - 3 = 9 (bút chì)
Số tiền mua 9 bút chì là:
114 000 - 51 000 = 63 000 (đồng)
Giá của 3 bút chì là:
63 000 : 9 × 3 = 21 000 (đồng)
Giá 10 quyển vở là:
51 000 - 21 000 = 30 000 (đồng)
Giá của 1 quyển vở là:
30 000 : 10 = 3000 (đồng)
Đáp số: 3000 đồng
Lời giải:
Giả sử bạn Lan mua số quyển vở và số bút gấp 5 lần: 15 vở và 25 bút
Giả sử bạn Bình mua số quyển vở và số bút gấp 3 lần: 15 vở và 9 bút
Số tiền tương ứng của bạn Lan là:
51 000 × 5 = 255 000 (đồng)
Số tiền tương ứng của bạn Bình là:
53 000 × 3 = 159 000 (đồng)
Số bút bạn Lan nhiều hơn số bút bạn Bình mua là:
25 - 9 = 16 (bút)
Số tiền bạn Lan mua bút nhiều hơn số tiền bạn Bình mua là:
255 000 - 159 000 = 96 000 (đồng)
Vậy giá mua cây bút chì là:
96 000 : 16 = 6000 (đồng)
Giá mua 3 cây bút chì là:
6000 × 3 = 18 000 (đồng)
Giá mua 1 quyển vở là:
(53 000 - 18 000) : 5 = 7000 (đồng)
Đáp số: Bút chì: 6 000 đồng;
Vở: 7000 đồng.
Lời giải:
Gọi a là số học sinh đồng diễn sau khi đã bớt 5 học sinh thừa.
Khi đó a vừa xếp đủ hàng thành 12, và hàng 15 mà không thừa ai. Do đó A chia hết cho 12 và 15, tức là chia hết cho 3, 4, 5 (hay là bội của 3 × 4 × 5 = 60)
Xét số học sinh là 60. Số hàng 15 là 4, số hàng 12 là 5, tức là ít hơn 1 hàng.
Để ít hơn 4 hàng thì cần 60 × 4 = 240 (học sinh)
Vậy số học sinh ban đầu đồng diễn là 240 + 5 = 245 học sinh
Lời giải:
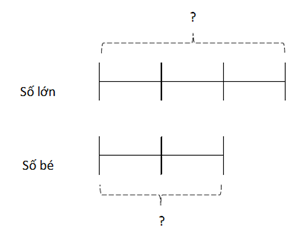
Coi hiệu của 2 số là 1 phần thì tổng của chúng là 5 phần.
Do đó số lớn là: (5 + 1) : 2 = 3 (phần)
Số bé là: 3 - 1 = 2 (phần)
Tích của hai số là: 2 × 3 = 6 (phần)
Mà tích hai số là 4008 nên giá trị một phần là:
4008 : 6 = 668
Số bé là: 668 × 2 =1336
Số lớn là: 668 × 3 = 2004
Đáp số: Số bé: 1336;
Số lớn là 2004
Lời giải:
Hàm số y = mx + 3 có các hệ số a = m, b = 3.
Hàm số y = (2m + 1)x - 5 có các hệ số a' = 2m + 1, b' = -5
Vì hai hàm số là hai hàm số bậc nhất nên a và a' phải khác 0, tức là:
m ≠ 0 và 2m + 1≠ 0 hay
m ≠ 0 và m≠−12
Theo đề bài ta có: b ≠ b' (vì 3 ≠ -5)
Vậy đồ thị của hai hàm số là đường thẳng song song với nhau khi và chỉ khi a ≠ a' tức là:
m = 2m + 1 ⇔ m = -1
Kết hợp với điều kiện ta thấy m = -1 là giá trị cần tìm
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.