Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 22) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 22)
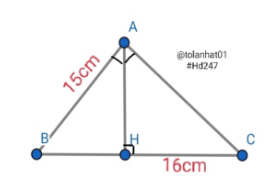
Câu 1: Cho vuông tại A có đường cao AH. Biết AC = 15cm; HB = 16cm. Tính BC; AB; AH; CH
Lời giải:
Ta có:
Áp dụng định lí Pytago vào vuông tại H, ta được:
hay AH = 12cm
Áp dụng định lí Pytago vào vuông tại H, ta được:
hay AB = 20cm
Ta có: BC = BH + HC
nên BC = 9 + 16 = 25cm
Câu 2: Cho vuông tại A đường cao AH. Biết AB = 15cm, HC = 16cm. Tính BC, AC, HC
Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông ABC có:
+ Xét tam giác vuông ABC có: AH . BC = AB . AC ( hệ thức lượng )
Vậy BC = 25(cm); AC = 20(cm); HC = 16(cm).
Lời giải:
Mỗi giờ vòi thứ nhất chảy được số phần bể là:
(bể)
Mỗi giờ vòi thứ hai chảy được số phần bể là:
(bể)
Mỗi giờ vòi thứ ba rút số phần bể là:
(bể)
Khi mở vòi I và vòi II mỗi giờ chảy được số phần bể là:
(bể)
Sau 3 giờ bể mở vòi I và vòi II bể chứa số nước là:
(bể)
Khi mở cả ba vòi thì mỗi giờ chảy được số phần bể là:
(bể)
Sau khi mở vòi thứ ba thì bể nước đầy sau số giờ là:
(giờ)
Lời giải:
Trong 1 giờ vòi I và II chảy được bể
Trong 1 giờ vòi II và III chảy được bể
Trong 1 giờ vòi III và I chảy được bể
Do đó trong 1 giờ cả 3 vòi chảy được
(bể)
Vậy thời gian để cả 3 vòi chảy đầy bể là 1:
(giờ) = 320 (phút)
b) Trong 1 giờ vòi III chảy được
(bể)
Lời giải:
Khi ta viết thêm vào bên trái số đó 1 thì tổng của số mới và số đã cho là:
(168 - 100) : 2 = 34
Đáp số: 34
Lời giải:
Đặt g(x) = f(x) – 10 (bậc 4)
(m là hằng số)
Vậy A = 336(9 − m) + 336(m + 5) – 20 = 4684
Câu 7: Tìm 4 số lập thành một CSN biết tổng bốn số bằng 15 và tổng các bình phương của chúng bằng 85
Lời giải:
Giả sử 4 số cần tìm là
Theo Đề bài ta có:
Với ta có CSN: 1; 2; 4; 8
Với ta có CSN: 8; 4; 2; 1
A.3,5 m
B.7 m
C.14 m
D.9 m
Lời giải:
Trung bình cộng hai đáy của hình thang là: 7 : 2 = 3,5 (m)
Đáp án cần chọn là: A
Lời giải:
Đặt
Cộng 1 vào ta được
Thay vào P ta được
Câu 10: Tìm x biết 135 - 5(x + 4) = 35
Lời giải:
135 - 5(x + 4) = 35
5(x + 4) = 135 - 35
5(x + 4) = 100
x + 4 = 100 : 5
x + 4 = 20
x = 20 - 4
x = 16
Câu 11: Có 4 đội bóng đá thi đấu vòng tròn( hai đội bất kì đều gặp nhau một trận)
a) Hỏi có bao nhiêu trận.
b) Câu hỏi với n đội bóng thi đấu vòng tròn thì có tất cả bao nhiêu trận
Lời giải:
a) Có 4 đội bóng thi đấu với nhau mà mỗi đội đều được đá với 3 đội còn lại nên số trận đấu là:
4 x 3 = 12 ( trận đấu )
Nhưng do mỗi trận đã bị tính hai lần nên số trận đấu là:
12 : 2 = 6 ( trận đấu )
b) Tương tự như câu a ta sẽ có công thức tổng quát cho n đội
n ( n - 1 ) : 2 ( trận đấu )
Lời giải:
Tổng số trận trong bảng đấu là: 4 . 3 : 2 = 6 ( trận)
Tổng số điểm trong trận thắng ( cũng như trận thua) là: 3 + 0 = 3 ( điểm)
Tổng số điểm trong trận hòa là: 1 + 1 = 2 ( điểm)
Nếu cả 6 trận đều thắng thì có tổng số điểm là: 6 . 3 = 18 ( điểm)
Số điểm còn thiếu là: 18 – 16 = 2 ( điểm)
Có số trận hòa là: 2 : 1 = 2 ( trận)
Vậy có 2 trận hòa
Câu 13: Cho tam giác ABC có AB = 2, AC = 3, . Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn
a) Tính
b) Biểu diễn theo
c) Chứng minh
Lời giải:
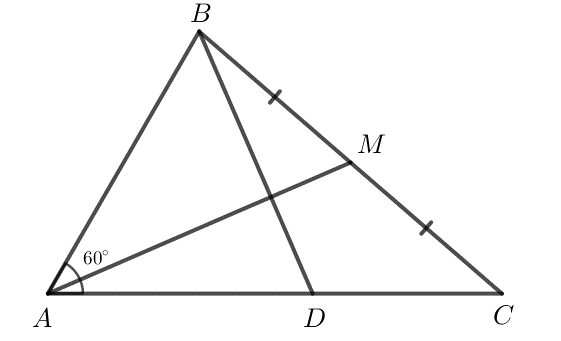
a) Ta có
Vậy
b) Do M là trung điểm của BC nên
Ta có
c) Ta có
Do đó .
Câu 14: Khoanh vào chữ đặt trước câu trả lời đúng:
Có 20 viên bi, trong đó có 3 viên bi nâu, 4 viên bi xanh, 5 viên bi đỏ, 8 viên bi vàng. Như vậy, 1515 số viên bi có màu:
A. Nâu
B. Xanh
C. Đỏ
D. Vàng
Lời giải:
số viên bi có màu nâu.
số viên bi có màu xanh
số viên bi có màu đỏ.
số viên bi có màu vàng.
Khoanh vào B.
Lời giải:
Ta có:
Gọi số túi mà Hoa chia được là x (túi)
Vì số bi mỗi màu ở mỗi túi cũng bằng nhau nên và
ƯC(48; 30; 60)
Vì x là lớn nhất nên x = ƯCLN(48; 30; 60)
Ta có: 48 = 24 . 3; 30 = 2 . 3 . 5; 60 = 22 . 3 . 5
x = ƯCLN(48; 30; 60) = 2 . 3 = 6 .
Vậy Hoa chia được nhiều nhất là 6 túi mà mỗi túi có số bi mỗi màu bằng nhau.
Đáp án cần chọn là: A
Câu 16: Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng
(d) : y = (m - 3)x + 1 bằng
Lời giải:
Gọi A là giao điểm của d với Ox
Gọi B là giao điểm của d với Oy
Từ O kẻ OH vuông góc AB
Áp dụng hệ thức lượng trong tam giác vuông OAB:
Câu 17: Tìm m để khoảng cách từ gốc tọa độ O đến đồ thị hàm số (1) bằng
Lời giải:
Điều kiện
Gọi A, B lần lượt là các giao điểm của đường thẳng (1) với các trục Ox, Oy.
Khi đó ta có:
Gọi H là hình chiếu của O trên đường thẳng (1)
Khi đó ta có vuông tại O và có đường cao OH.
Áp dụng hệ thức lượng cho vuông tại O và có đường cao OH ta có:
Vậy thỏa mãn điều kiện bài toán.
Chọn C.
Lời giải:
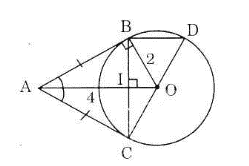
Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét có :
CI = IB
CO = OD (bán kính)
⇒ BD // HO (HO là đường trung bình của BCD) ⇒ BD // AO.
a) Biểu diễn AB, AC theo hai vectơ và biểu diễn AJ qua AB, AC
b) Biểu diễn AG theo hai vectơ
Lời giải:
a) I là điểm trên cạnh BC mà:
Tương tự
J là điểm trên BC kéo dài:
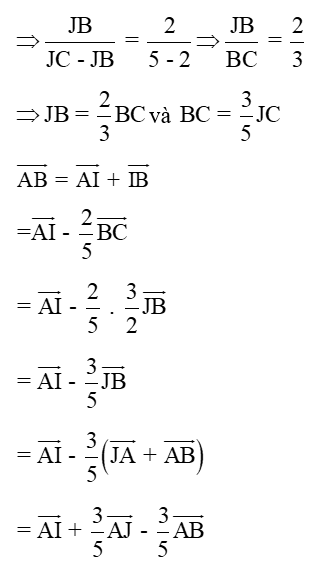
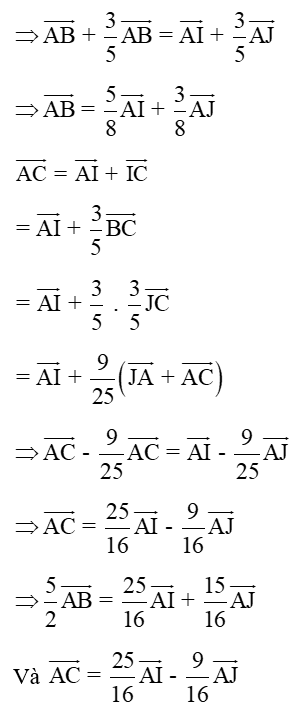

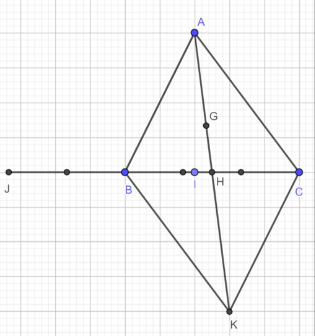
Lời giải:
- Tìm điểm A’ đối xứng với A qua d
- Nối A’B cắt d tại M. M chính là điểm cần tìm.
- Thật vậy : Vì A’ đối xứng với A qua d cho nên MA = MA’.
Do đó : MA + MB = MA’ + MB = A’B .
- Giả sử tồn tại M’ khác M thuộc d thì : M’A + M’B = M’A’ + M’B lớn hơn hoặc bằng A'B. Dấu bằng chỉ xảy ra khi A’M’B thẳng hàng. Nghĩa là M trùng với M’
Câu 21: Cho hàm số y = f(x). Đồ thị của hàm số y = f’(x) như hình bên.
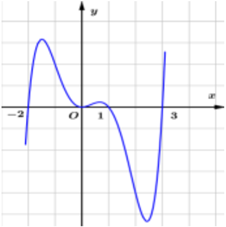
Hàm số g(x) = f(x2) có bao nhiêu điểm cực trị?
A. 4
B. 3
C. 5
D. 2
Lời giải:
Đáp án đúng là: C
Ta có g’(x) = 2x.f’(x2).
Cho g’(x) = 0 ⇔ 2x.f’(x2) = 0.
Bảng biến thiên:
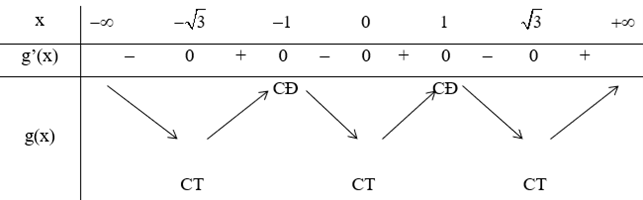
Dựa vào bảng biến thiên, ta thấy hàm số g(x) có tất cả 5 điểm cực trị.
Vậy ta chọn phương án C.
Câu 22: Phân tích đa thức thành nhân tử: 9x2 – 6xy + y2 – 81.
Lời giải:
9x2 – 6xy + y2 – 81 = (3x – y)2 – 92
= (3x – y – 9)(3x – y + 9).
Lời giải:
Ta có đồ thị của hàm số đã cho đi qua gốc tọa độ O(0; 0).
Suy ra 0 = (1 – 3m).0 + m + 3.
⇔ m = –3.
Vậy m = –3 thỏa mãn yêu cầu bài toán.
A. x + y + 2z – 3 = 0;
B. x + y + 2z – 6 = 0;
C. x + 3y + 4z – 7 = 0;
D. x + 3y + 4z – 26 = 0.
Lời giải:
Ta có .
Mặt phẳng (P) đi qua điểm A(0; 1; 1) và có vectơ pháp tuyến .
Suy ra phương trình mặt phẳng (P): 1.(x – 0) + 1.(y – 1) + 2.(z – 1) = 0.
⇔ x + y + 2z – 3 = 0.
Vậy ta chọn phương án A.
Câu 25: Giải phương trình sau: 16,7.Pn = 2004.Pn – 5.
Lời giải:
Ta có 16,7.Pn = 2004.Pn – 5 (Điều kiện: n ≥ 6).
⇔ 16,7.n! = 2004.(n – 5)!
⇔ 16,7.n.(n – 1)(n – 2)(n – 3)(n – 4)(n – 5)! = 2004.(n – 5)!
⇔ (n – 5)!.[16,7.n.(n – 1)(n – 2)(n – 3)(n – 4) – 2004] = 0
⇔ 16,7.n.(n – 1)(n – 2)(n – 3)(n – 4) – 2004 = 0
⇔ n.(n – 1)(n – 4)(n – 2)(n – 3) – 120 = 0
⇔ n.(n2 – 5n + 4)(n2 – 5n + 6) – 120 = 0
⇔ (n3 – 5n2 + 4n)(n2 – 5n + 6) – 120 = 0
⇔ n5 – 5n4 + 6n3 – 5n4 + 25n3 – 30n2 + 4n3 – 20n2 + 24n – 120 = 0
⇔ n5 – 10n4 + 35n3 – 50n2 + 24n – 120 = 0
⇔ (n5 – 5n4) – (5n4 – 25n3) + (10n3 – 50n2) + (24n – 120) = 0
⇔ n4.(n – 5) – 5n3.(n – 5) + 10n2.(n – 5) + 24(n – 5) = 0
⇔ (n – 5)(n4 – 5n3 + 10n2 + 24) = 0 (1)
Ta có .
Ta có
.
Khi đó phương trình (1) tương đương với: n – 5 = 0.
⇔ n = 5 (nhận).
Vậy phương trình đã cho có nghiệm là n = 5.
A. A(x – x0) + B(y0 – y) = 0;
B. x0(x – A) + y0(y – B) = 0;
C. B(x – x0) + A(y – y0) = 0;
D. A(x – x0) + B(y – y0) = 0.
Lời giải:
Ta có .
Ta có M(x; y) ∈ d.
⇔ A(x – x0) + B(y – y0) = 0.
Vậy điều kiện cần và đủ để điểm M(x; y) nằm trên đường thẳng d đi qua điểm M(x0; y0) và có vectơ pháp tuyến là A(x – x0) + B(y – y0) = 0.
Do đó ta chọn phương án D.
Lời giải:
Ta có a2 – 2b = c2 – 2a.
⇔ a2 – c2 = 2b – 2a.
⇔ (a – c)(a + c) = 2(b – a)
Chứng minh tương tự, ta được và .
Ta có A = (a + b + 2)(b + c + 2)(c + a + 2).
= –2.2.2 = –8.
Vậy A = –8.
Lời giải:
Ta có u1 = 3.1 – 1 = 2 và u2 = 3.2 – 1 = 5.
Suy ra công sai d = u2 – u1 = 5 – 2 = 3.
Vậy số hạng đầu u1 = 2 và công sai d = 3.
Câu 29: Khảo sát sự biến thiên và vẽ đồ thị hàm số y = x2 – 2x – 3.
Lời giải:
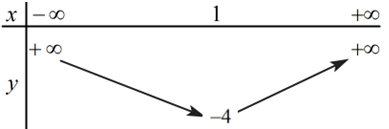
Tập xác định: D = ℝ.
Tọa độ đỉnh I(1; –4).
Sự biến thiên:
Do a = 1 > 0 nên hàm số đồng biến trên khoảng (1; +∞) và nghịch biến trên khoảng (–∞; 1).
Bảng biến thiên:
Điểm đặc biệt:
|
x |
–1 |
0 |
1 |
2 |
3 |
|
y = x2 – 2x – 3 |
0 |
–3 |
–4 |
–3 |
0 |
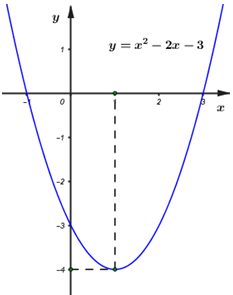
Đồ thị:
Đồ thị hàm số là đường parabol có đỉnh I(1; –4), hướng bề lõm lên trên và nhận đường thẳng x = 1 làm trục đối xứng.
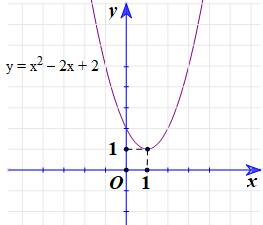
Câu 30: Vẽ đồ thị hàm số f(x) = x2 – 2x + 2.
Lời giải:
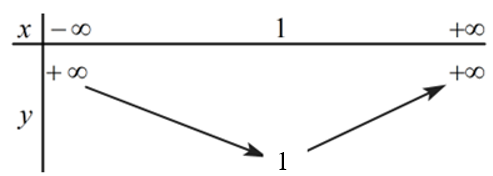
Tập xác định: D = ℝ.
Tọa độ đỉnh I(1; 1).
Sự biến thiên:
Do a = 1 > 0 nên hàm số đồng biến trên khoảng (1; +∞) và nghịch biến trên khoảng (–∞; 1).
Bảng biến thiên:
Điểm đặc biệt:
|
x |
–1 |
0 |
1 |
2 |
3 |
|
f(x) = x2 – 2x + 2 |
5 |
2 |
1 |
2 |
5 |
Đồ thị:
Đồ thị hàm số là đường parabol có đỉnh I(1; 1), hướng bề lõm lên trên và nhận đường thẳng x = 1 làm trục đối xứng.
Câu 31: Chứng minh rằng: a4 + b4 + c4 ≥ abc(a + b + c).
Lời giải:
Áp dụng bất đẳng thức:
a2 + b2 + c2 ≥ ab + ac + bc
⇒ a4 + b4 + c4 ≥ a2b2 + a2c2 + b2c2
Mà: a2b2 + a2c2 + b2c2 ≥ a2bc + ab2c + abc2
Mặc khác: a2bc + ab2c + abc2 = abc(a + b + c).
Vậy: a4 + b4 + c4 ≥ abc(a + b + c).
Lời giải:
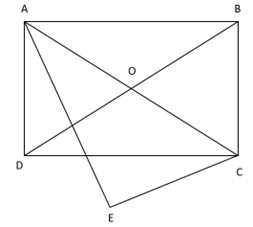
Vì ABCD là hình chữ nhật nên nội tiếp đường tròn .
Xét tứ giác ADEC có
Do đó tứ giác ADEC nội tiếp
Vậy 5 điểm A, B, C, D, E cung thuộc đường tròn .
a) A = x2 + 4y2 – 4x + 32y + 2078;
b) B = 3x2 + y2 + 4x – y .
Lời giải:
a) Ta có A = x2 + 4y2 – 4x + 32y + 2078
= (x2 – 4x +2) + (4y2 + 32y + 64) + 2010
= (x – 2)2 + (2y + 8)2 + 2010
Vì (x – 2)2 ≥ 0; (2y + 8)2 ≥ 0 nên A = (x – 2)2 + (2y + 8)2 + 2010 ≥ 2010.
Dấu = xảy ra khi x – 2 = 0 và 2y + 8 = 0.
Vây Amin = 2010 ⇔ (x; y) = (2; – 4).
b) Ta có: B = 3x2 + y2 + 4x – y
Dấu = xảy ra khi ; .
Vậy .
Lời giải:
Ở phép chia lần thứ hai khi cùng giảm cả số bị chia và số chia đi 5 thì thương số là 75 số dư là 4 nên thương và số dư không thay đổi.
Suy ra ở phép chia lần thức nhất thương ban đầu vẫn là 75 và số dư ban đầu là 4.
Vì số dư lớn nhất là 4 nên số bị chia là 5.
Số chia ban đầu là: 75 × 5 + 4 = 379.
Vậy phép chia ban đầu là 379 : 5 = 75 dư 4.
Lời giải:
Ở phép chia mới khi cùng giảm cả số bị chia và số chia đi 2 thì thương số là 162 số dư là 10 nên thương và số dư không thay đổi.
Suy ra ở phép chia lần thức nhất thương ban đầu vẫn là 162 và số dư ban đầu là 10.
Vì số dư lớn nhất là 10 nên số bị chia là 11.
Số chia ban đầu là: 162 × 11 + 10 = 1792.
Vậy phép chia ban đầu là 1792 : 11 = 162 dư 10.
Câu 36: 25% của số đó là 40. Số đó là số nào?
Lời giải:
Vì 25% của số đó là 40.
Vậy số đã cho là: 40 : 25% = 160.
Đáp số: 160.
Câu 37: Biết 25% của 1 số là 40. Tính số đó.
Lời giải:
Vì 25% của số là 40 nên giá trị của số đó là: 40 : 25% = 160
Giá trị của số đó là: .
Đáp số: 32.
Lời giải:
Điều kiện xác định của hàm số :
Vậy để hàm số xác định trên khoảng (−1;1) .
Câu 39: Cho hàm số f(x) xác định trên . Trong các khẳng định sau, khẳng định nào đúng?
A. Nếu hàm số f(x) liên tục trên đoạn và f(a).f(b) > 0 thì phương trình f(x) = 0 không có nghiệm trong khoảng (a; b);
B. Nếu f(a).f(b) < 0 thì phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (a;b);
C. Nếu phương trình f(x) = 0 có nghiệm trong khoảng (a; b) thì hàm số y = f(x) liên tục trên khoảng (a;b);
D. Nếu hàm số y = f(x) liên tục tăng trên đoạn và f(a).f(b) > 0 thì phương trình f(x) = 0 không thể có nghiệm trong (a; b).
Lời giải:
Đáp án D đúng vì : hàm số y = f(x) liên tục tăng trên đoạn nên f(a) < f(x) < f(b) ∀x ∈ (a; b).
Ta có: f(a).f(b) > 0
Vậy f(x) = 0 không thể có nghiệm trong (a; b).
Câu 40: Phân tích đa thức thành nhân tử: a(a + 2b)3 − b(2a + b)3 .
Lời giải:
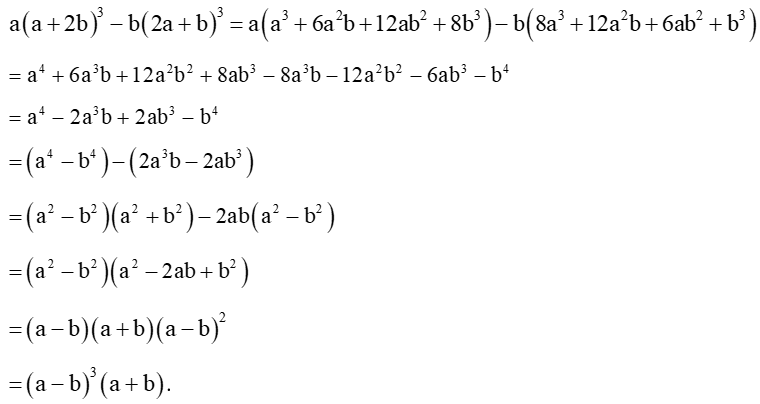
A. 2%;
B. 1,7%;
C. 5,9%;
D. 1,2%.
Lời giải:
Sai số tỉ đối của phép đo đó là: .
Đáp án đúng là B.
A. 2%;
B. 1,7%;
C. 0,6%;
D. 1,3%.
Lời giải:
Sai số tương đối của phép đo đó là: .
Đáp án đúng là D.
Câu 43: Tìm số tự nhiên a nhỏ nhất có ba chữ số. Biết rằng a chia cho 11 dư 3 và a chia cho 13 dư 5.
Lời giải:
Gọi số cần tìm là a thì a + 8 ∈ BC (11; 13) và a là số nhỏ nhất thỏa mãn 100 ≤ a ≤ 999.
Ta có BCNN (11; 13) = 11.13 = 143.
BC (11;13) ∈ {0; 143; 286; ...}.
Vì a là số tự nhiên có ba chữ số nhỏ nhất nên a + 8 = 143 ⇒ a = 135.
Vậy số cần tìm là 135.
Câu 44: Cho 2 đường thẳng (d): y = – x + m + 2 và (d'): y= (m2 – 2).x + 1.
a) Khi m = – 2, hãy tìm tọa độ giao điểm của hai đường thẳng.
b) Tìm m để (d) song song với (d').
Lời giải:
a) m = – 2 thì (d): y = − x; (d'): y = 2x + 1.
Gọi M (x0; y0) là giao điểm của 2 đường thẳng (d) và (d')
⇒ (d): y0 = – x0 ; (d'): y0 = 2x0 + 1
Vậy tọa độ giao điểm của 2 đường thẳng trên là: .
b) Điều kiện để (d) song song với (d'):
Vậy m = 1 thì (d) song song với (d').
Câu 45: Tam giác ABC vuông tại A có AB = 6 cm; AC = 8 cm và BC = 10 cm. Đường cao AH dài là:
А. 4,8 сm;
В. 9,6 сm;
С. 8,4 cm;
D. 8,4 m.
Lời giải:
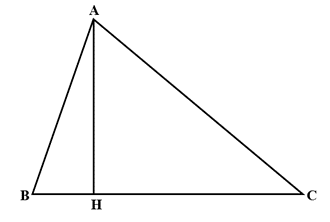
Độ dài đường cao AH của tam giác ABC vuông tại A là:
(cm).
Đáp án đúng là A.
Lời giải:
Số các chọn 3 học sinh vào mỗi tổ: .
Chia 3 bạn nữ vào 3 tổ: 3! = 6
Xếp 6 bạn nam vào 3 tổ: .
Xác suất: .
Lời giải:
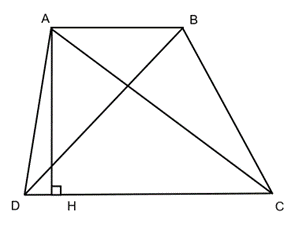
Chiều cao hình thang ABCD là: 225.2 : ( 12 + 18 ) = 15 (cm)
Ta có: Chiều cao của hình thang ABCD chính là chiều cao của hình tam giác ACD và độ dài đáy của hình tam giác ACD bằng 18 cm.
Diện tích hình tam giác ACD là : 15.18 : 2 = 135 (m2).
Diện tích hình tam giác ABC là : 225 − 135 = 90 (m2).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.