Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24)

Ngọc Nguyễn Ngày: 13-06-2023 Tổng hợp kiến thức

426

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24)

Câu 1: Cho phương trình (m – 4)x² – 2m(m – 2)x + m – 1 = 0. Định m để phương trình có hai nghiệm trái dấu và nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương.

Lời giải:

Phương trình đã cho có hai nghiệm trái dấu $\Leftrightarrow \{\begin{cases} a \neq 0 \\ P < 0 \end{cases}$ .

$\Leftrightarrow \{\begin{cases} m - 4 \neq 0 \\ \frac{m - 1}{m - 4} < 0 \end{cases} \Leftrightarrow \{\begin{cases} m \neq 4 \\ 1 < m < 4 \end{cases} \Leftrightarrow 1 < m < 4$ (1)

Phương trình đã cho có nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương.

⇔ S < 0 $\Leftrightarrow \frac{2 m (m - 2)}{m - 4} < 0 \Leftrightarrow 2 m (m - 2) > 0$ (do theo (1) thì m – 4 < 0)

$\Leftrightarrow \frac{2 m (m - 2)}{m - 4} < 0 \Leftrightarrow 2 m (m - 2) > 0$ (2)

Từ (1), (2), suy ra 2 < m < 4.

Vậy 2 < m < 4 thỏa mãn yêu cầu bài toán.

Câu 2: Trong các nhóm hình sau, nhóm nào có tâm đối xứng?

A. Hình thang cân, hình thoi, hình bình hành;

B. Hình vuông, hình chữ nhật, hình thang cân;

C. Hình thang vuông, hình bình hành, hình thoi;

D. Hình bình hành, hình chữ nhật, hình vuông.

Lời giải:

Đáp án đúng là: D

Tâm đối xứng của hình bình hành, hình chữ nhật, hình thoi, hình vuông là giao điểm của hai đường chéo.

Tâm đối xứng của đường tròn là tâm của đường tròn đó.

Vậy ta chọn phương án D.

Câu 3: Nhóm hình nào đều có trục đối xứng?

A. Hình thang cân, hình chữ nhật, hình thoi, hình vuông;

B. Hình thang cân, hình thoi, hình vuông, hình bình hành;

C. Hình bình hành, hình thang cân, hình chữ nhật;

D. Hình thang cân, hình chữ nhật, hình bình hành, hình vuông.

Lời giải:

Đáp án đúng là: A

Vì hình bình hành không có trục đối xứng nên ta loại các phương án B, C, D.

Vậy ta chọn phương án A.

Câu 4: Tìm ảnh của đường tròn (C): (x + 1)² + (y – 1)² = 4 qua:

a) Q_{(O; 90°)};

b) Q_{(O; 45°)}.

Lời giải:

a) Gọi (C’) là ảnh của (C) qua phép quay Q_{(O; 90°)}.

Suy ra (C’) có bán kính R’ = R = 2 và có tâm I’ = Q_{(O; 90°)}(I).

Do đó tọa độ I’(–1; –1).

Vậy phương trình (C’): (x + 1)² + (y + 1)² = 4.

b) Gọi (C’’) là ảnh của (C) qua phép quay Q_{(O; 45°)}.

Suy ra (C’’) có bán kính R’’ = R = 2 và có tâm I’’ = Q_{(O; 45°)}(I).

Khi đó $\{\begin{cases} x_{{I^{'}}^{'}} = x_{I} \cos 45 ° - y_{I} \sin 45 ° = - 1. \frac{\sqrt{2}}{2} - 1. \frac{\sqrt{2}}{2} = - \sqrt{2} \\ y_{{I^{'}}^{'}} = x_{I} \sin 45 ° + y_{I} \cos 45 ° = - 1. \frac{\sqrt{2}}{2} + 1. \frac{\sqrt{2}}{2} = 0 \end{cases}$

Vì vậy tọa độ ${I^{'}}^{'} (- \sqrt{2}; 0)$ .

Vậy phương trình (C’’): ${(x + \sqrt{2})}^{2} + y^{2} = 4$ .

Câu 5: Tìm ảnh của (C): x² + y² + 2x – 84 = 0 qua Q_{(O; –45°)}.

Lời giải:

Gọi (C’) là ảnh của (C) qua phép quay Q_{(O; –45°)}.

Suy ra (C’) có bán kính $R = \sqrt{85}$ và có tâm I’ = Q_{(O; –45°)}(I).

Khi đó $\{\begin{cases} x_{I^{'}} = x_{I} \cos (- 45 °) - y_{I} \sin (- 45 °) = - 1. \frac{\sqrt{2}}{2} + 0. \frac{\sqrt{2}}{2} = - \frac{\sqrt{2}}{2} \\ y_{I^{'}} = x_{I} \sin (- 45 °) + y_{I} \cos (- 45 °) = 1. \frac{\sqrt{2}}{2} + 0. \frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{2} \end{cases}$

Vì vậy tọa độ $I^{'} (- \frac{\sqrt{2}}{2}; \frac{\sqrt{2}}{2})$ .

Vậy phương trình (C’): ${(x + \frac{\sqrt{2}}{2})}^{2} + {(y - \frac{\sqrt{2}}{2})}^{2} = 85$ .

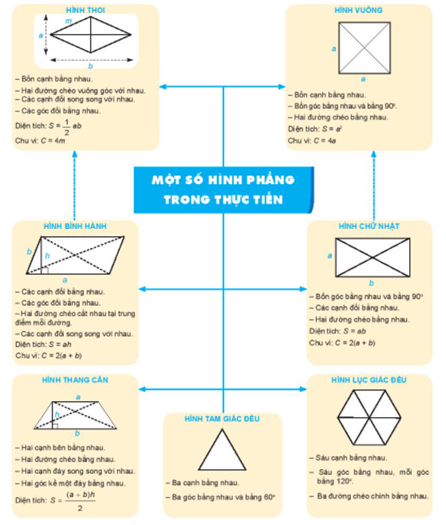
Câu 6: Sơ đồ tư duy chương 4 hình học lớp 6.

Lời giải:

Sơ đồ tư duy chương IV – Một số hình phẳng trong thực tiễn – Toán 6.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 1)

Câu 7: Cách chuyển hỗn số thành số thập phân, ta làm như thế nào?

Lời giải:

Muốn đổi hỗn số thành số thập phân, ta làm các bước sau:

Bước 1: Đưa hỗn số thành phân số:

– Lấy phần nguyên nhân với mẫu số, kết quả nhận được cộng thêm tử số;

– Thay kết quả ở trên thành tử số mới, giữ nguyên mẫu số, ta được một phân số từ hỗn số đã cho.

Bước 2: Đưa mẫu số về 10; 100; 1000; … và thực hiện đổi phân số thập phân về số thập phân.

Ví dụ: Đổi các hỗn số $5 \frac{1}{10}$ và $5 \frac{3}{4}$ thành số thập phân.

Hướng dẫn giải

Ta có: $5 \frac{1}{10} = \frac{5 \times 10 + 1}{10} = \frac{51}{10} = 5,1$ ;

$5 \frac{3}{4} = \frac{5 \times 4 + 3}{4} = \frac{23}{4} = \frac{23 \times 25}{4 \times 25} = \frac{575}{100} = 5,75$ .

Câu 8: Cho hình bình hành có AB = 2AD. Gọi M, N theo thứ tự là trung điểm của AB và CD.

a) Chứng minh tứ giác AMCN là hình bình hành.

b) Chứng minh AN vuông góc với DM.

c) Gọi E là giao điểm của AN và DM, F là giao điểm của MC và BN. Chứng minh EF = MN.

d) Chứng minh diện tích hình bình hành ABCD gấp 4 lần diện tích tam giác ADN.

Lời giải:

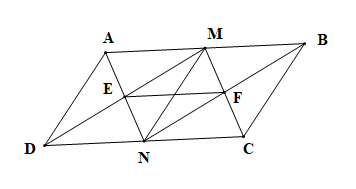
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 2)

a) Vì ABCD là hình bình hành

Nên AB = CD, AB // CD

Vì M, N theo thứ tự là trung điểm của AB và CD

Nên AM = MB = $\frac{1}{2}$ AB, CN = DN = $\frac{1}{2}$ CD

Mà AB = CD (chứng minh trên)

Suy ra AM = CN = MB = DN

Xét tứ giác AMCN có

AM = CN, AM // CN (chứng minh trên)

Suy ra AMCN là hình bình hành

Vậy AMCN là hình bình hành.

b) Xét tứ giác AMND có

AM = DN, AM // DN (chứng minh trên)

Suy ra AMND là hình bình hành

Ta có AB = 2AM, AB = 2AD

Suy ra AM = AD

Mà AMND là hình bình hành

Do đó AMND là hình thoi

Lại có AN, DM là hai đường chéo

Suy ra AN ⊥ DM

Vậy AN ⊥ DM.

c) Xét tứ giác BMNC có

BM = CN, BM // CN (chứng minh câu a)

Suy ra BMNC là hình bình hành

Mà hai đường chéo MC và BN cắt nhau tại F

Suy ra F là trung điểm của MC, BN

Do đó MF = $\frac{1}{2}$ MC

Vì AMND là hình bình hành có hai đường chéo AN, DM cắt nhau tại E

Nên E là trung điểm của AN

Suy ra NE = $\frac{1}{2}$ AN

Vì AMCN là hình bình hành nên AN // CM, AN = CM

Ta có MF = $\frac{1}{2}$ MC, NE = $\frac{1}{2}$ AN, AN = CM

Suy ra MF = NE

Xét tứ giác EMFN có

FM = EN, FM // EN (chứng minh trên)

Suy ra EMFN là hình bình hành

Mà $\hat{M E N} = 90 °$ (do AN ⊥ DM)

Do đó EMFN là hình chữ nhật

Lại có MN và EF là hai đường chéo

Suy ra MN = FE

Vậy MN = FE.

d) Gọi h là chiều cao của hình bình hành ABCD kẻ từ A

Ta có $\frac{S_{A B C D}}{S_{A D N}} = \frac{h . C D}{\frac{1}{2} h . D N} = \frac{2 C D}{D N} = \frac{2.2 D N}{D N} = 4$

Suy ra S_ABCD= 4 S_ADN

Vậy diện tích hình bình hành ABCD gấp 4 lần diện tích tam giác ADN.

Câu 9: Cho tam giác ABC vuông tại A biết AB = 3 cm, AC = 4 cm.

Tính tỉ số lượng giác của góc B và góc C.

Lời giải:

Áp dụng định lý Pytago trong tam giác vuông ABC ta có

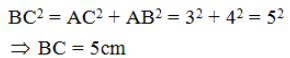
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 3)

Xét tam giác ABC vuông tại A có

sin B = cos C = $\frac{A C}{B C} = \frac{4}{5}$

cos B = sin C = $\frac{A B}{B C} = \frac{3}{5}$

tan B = cot C = $\frac{A C}{B A} = \frac{4}{3}$

cot B = tan C = $\frac{A B}{A C} = \frac{3}{4}$

Câu 10: Chứng minh rằng hai tam giác ABC và MNP có cùng trọng tâm khi và chỉ khi $\vec{A M} + \vec{B N} + \vec{C P} = \vec{0}$

Lời giải:

Gọi G là trọng tâm tam giác ABC, G’ là trọng tâm tam giác MNP

Ta có:

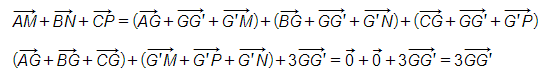
1500 câu hỏi ôn tập môn Toán có đáp án (Phần 13) (ảnh 1)

hai tam giác ABC và MNP có cùng trọng tâm khi và chỉ khi G ≡ G’

$\Leftrightarrow \vec{G G'} = \vec{0} \Leftrightarrow \vec{A M} + \vec{B N} + \vec{C P} = \vec{0}$

Vậy hai tam giác ABC và MNP có cùng trọng tâm khi và chỉ khi $\vec{A M} + \vec{B N} + \vec{C P} = \vec{0}$

Câu 11: Cho tam giác ABC. Lấy các điểm M, N, P thỏa mãn $\vec{A M} = \vec{A B} - 2 \vec{B C}, \vec{B N} = 3 \vec{B C} + \vec{A C}, \vec{C P} = 2 \vec{C A}$ . Chứng minh hai tam giác ABC và MNP có cùng trọng tâm.

Lời giải:

Ta có

$\vec{A M} + \vec{B N} + \vec{C P} = \vec{A B} - 2 \vec{B C} + 3 \vec{B C} + \vec{A C} + 2 \vec{C A} \vec{A B} - 2 \vec{B C} + 3 \vec{B C} + \vec{A C} + 2 \vec{C A} = \vec{A B} + \vec{B C} + \vec{C A} = \vec{A C} + \vec{C A} = \vec{0}$

Suy ra hai tam giác ABC và MNP có cùng trọng tâm

Vậy hai tam giác ABC và MNP có cùng trọng tâm.

Câu 12: Tìm tích của số chẵn lớn nhất có hai chữ số và số lớn nhất có một chữ số.

Lời giải:

Số chẵn lớn nhất có hai chữ số là 98

Số lớn nhất có một chữ số là 9

Tích của số chẵn lớn nhất có hai chữ số và số lớn nhất có một chữ số là:

98 x 9 = 882

Vậy tích của số chẵn lớn nhất có hai chữ số và số lớn nhất có một chữ số bằng 882.

Câu 13: Tập xác định D của hàm số $y = {(x^{2} - 3 x + 2)}^{π}$

A. (– ∞; 1) ∪ (2; + ∞);

B. ℝ;

C. (0; + ∞);

D. (1; 2).

Lời giải:

Đáp án đúng là: A

Hàm số $y = {(x^{2} - 3 x + 2)}^{π}$ là hàm lũy thừa có số mũ π nên hàm số xác định khi

x² – 3x + 2 > 0 ⇔ (x – 1)(x – 2) > 0

⇔ $[\begin{array}{l} x < 1 \\ x > 2 \end{array}$ ⇔ x ∈ (– ∞; 1) ∪ (2; + ∞)

Vậy ta chọn đáp án A.

Câu 14: Tìm tập xác định của hàm số sau: y = x² – 3x +2

Lời giải:

Hàm số y = x² – 3x +2 luôn xác định với mọi giá trị của x

Vậy tập xác định của hàm số là D = ℝ.

Câu 15: Thế nào thế nào là hai đa thức đồng dạng? Cho ví dụ?

Lời giải:

Hai đơn thức đồng dạng là hai đơn thức có hệ số khác không và có cùng phần biến

Ví dụ: 2x2y, – 3x5y, 7x4y là các đơn thức đồng dạng.

Câu 16: Rút gọn $A = \frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{3} - 1}$

Lời giải:

$A = \frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{3} - 1} A = \frac{\sqrt{3} - 1 + \sqrt{3} + 1}{(\sqrt{3} + 1) (\sqrt{3} - 1)} A = \frac{2 \sqrt{3}}{3 - 1} A = \frac{2 \sqrt{3}}{2} = \sqrt{3}$

Vậy A = $\sqrt{3}$ .

Câu 17: Tính:

2m² 85 cm² = ............. m²

2m² 85 dm² = ............. m²

$\frac{85}{100}$ ha = ...................km

Lời giải:

Ta có

2m² 85 cm² = 2,008 5 m²

2m² 85 dm² = 2,85 m²

$\frac{85}{100}$ ha = 0,008 5 km.

Câu 18: Tìm số nguyên x, biết 2x chia hết cho (x – 1)

Lời giải:

Ta có 2x ⋮ x – 1

⇔ 2x – 2 + 2 ⋮ x – 1

⇔ 2(x – 1) + 2 ⋮ x – 1

⇔ 2 ⋮ x – 1 (vì 2(x – 1) ⋮ x – 1)

⇔ x – 1 ∈ Ư(2)

⇔ x – 1 ∈ {1; 2; – 1; – 2}

⇔ x ∈ {2; 3; 0; – 1}

Vậy x ∈ {2; 3; 0; – 1}.

Câu 19: Tìm số nguyên x, biết (2x + 1) chia hết cho (x – 1)

Lời giải:

Ta có 2x + 1 ⋮ x – 1

⇔ 2x – 2 + 3 ⋮ x – 1

⇔ 2(x – 1) + 3 ⋮ x – 1

⇔ 3 ⋮ x – 1 (vì 2(x – 1) ⋮ x – 1)

⇔ x – 1 ∈ Ư(3)

⇔ x – 1 ∈ {1; 3; – 1; – 3}

⇔ x ∈ {2; 4; 0; – 2}

Vậy x ∈ {2; 4; 0; – 2}.

Câu 20: Điền vào chỗ trống

3,4 giờ = .... giờ .....phút

Lời giải:

Ta có 1 giờ = 60 phút

Nên 3,4 giờ = 3 giờ 24 phút

Vậy 3,4 giờ = 3 giờ 24 phút.

Câu 21: Giải phương trình : $A_{x}^{3} + C_{x}^{x - 2} = 14 x$

Lời giải:

Điều kiện xác định x ∈ N, x > 3

Ta có $A_{x}^{3} + C_{x}^{x - 3} = 14 x$

⇔ x(x – 1)(x – 2) + $\frac{x (x - 1)}{2!}$ = 14x

⇔ (x – 1)(x – 2) + $\frac{x - 1}{2}$ = 14

⇔ 2(x – 1)(x – 2) + (x – 1)= 28

⇔ 2x² – 4x – 2x + 4 + x – 1 = 28

⇔ 2x² – 5x – 25 = 0

⇔ (x – 5)(2x + 5) = 0

⇔ $[\begin{array}{l} x = 5 \\ x = - \frac{5}{2} \end{array}$

Mà x > 3 nên x = 5

Vậy x = 5.

Câu 22: Giải phương trình : $A_{x}^{3} + C_{x}^{x - 3} = 14 x$ (x là ẩn số)

A. x = 5 và x = – 2

B. x = 5

C. x = – 2

D. Vô nghiệm.

Lời giải:

Đáp án đúng là B

Điều kiện xác định x ∈ N, x ≥ 3

Ta có $A_{x}^{3} + C_{x}^{x - 3} = 14 x$

⇔ x(x – 1)(x – 2) + $\frac{x (x - 1) (x - 2)}{3!}$ = 14x

⇔ (x – 1)(x – 2) + $\frac{(x - 1) (x - 2)}{6}$ = 14

⇔ 6(x – 1)(x – 2) + (x – 1)(x – 2) = 84

⇔ 7(x – 1)(x – 2) = 84

⇔ (x – 1)(x – 2) = 12

⇔ x² – 2x – x +2 = 12

⇔ x² – 3x – 10 = 0

⇔ (x – 5)(x + 2) = 0

⇔ $[\begin{array}{l} x = 5 \\ x = - 2 \end{array}$

Mà x ≥ 3 nên x = 5

Vậy ta chọn đáp án B.

Câu 23: Có thể viết được bao nhiêu phân số có tử số và mẫu số là 1 hoặc 2?

Lời giải:

Ta viết được 4 phân số có tử số và mẫu số là 1 hoặc 2 là $\frac{1}{2}, \frac{2}{1}, \frac{12}{1}, \frac{1}{12}$ .

Câu 24: Giải phương trình $\sqrt{3}$ cos 2x – sin 2x = $\sqrt{2}$

Lời giải:

Ta có:

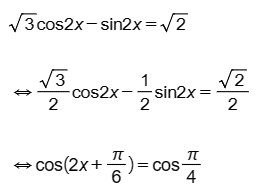
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 4)

$\Leftrightarrow [\begin{array}{l} 2 x + \frac{π}{6} = \frac{π}{4} + k 2 π \\ 2 x + \frac{π}{6} = - \frac{π}{4} + k 2 π \end{array} \Leftrightarrow [\begin{array}{l} 2 x = \frac{π}{4} - \frac{π}{6} + k 2 π \\ 2 x = - \frac{π}{4} - \frac{π}{6} + k 2 π \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{π}{24} + k π \\ x = \frac{- 5 π}{24} + k π \end{array}$

Vậy phương trình có nghiệm x = $\frac{π}{24} + k π$ , x = $\frac{- 5 π}{24} + k π$ .

Câu 25: Giải phương trình: cos 2x – $\sqrt{3}$ sin2x = 2

Lời giải:

Ta có:

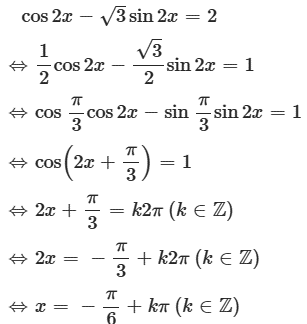
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 5)

Vậy phương trình có nghiệm $x = - \frac{π}{6} + k π$ , k ∈ Z.

Câu 26: Tìm m để ba điểm A (2; – 1), B (1; 1), C (3, m + 1) thẳng hàng.

Lời giải:

Phương trình đường thẳng AB có dạng y = ax + b

A (2; – 1) nên 2a + b = – 1

B (1; 1) nên a + b = 1

Suy ra $\{\begin{cases} 2 a + b = - 1 \\ a + b = 1 \end{cases} \Leftrightarrow \{\begin{cases} 2 a + 1 - a = - 1 \\ b = 1 - a \end{cases} \Leftrightarrow \{\begin{cases} a = - 2 \\ b = 1 - a \end{cases} \Leftrightarrow \{\begin{cases} a = - 2 \\ b = 3 \end{cases}$

Do đó y = – 2x + 3

Để 3 điểm A, B, C thẳng hàng thì C (3, m + 1) thuộc đường thẳng AB

Suy ra m + 1 = – 2 . 3 + 3

⇔ m = – 4

Vậy m = – 4.

Câu 27: Theo dõi thời gian làm bài tập (tính theo phút) của 30 học sinh (ai cũng làm được) và ghi lại như sau:

10 5 8 8 9 7 8 9 14 7

5 7 8 10 9 8 10 7 14 8

9 8 9 9 9 9 10 5 5 14

a) Bảng trên được gọi là bảng gì? Dấu hiệu cần tìm hiểu ở đây là gì?

b) Lập bảng “ tần số ” và tính số trung bình cộng

c) Tìm mốt của dấu hiệu và nêu nhận xét

d) Vẽ biểu đồ đoạn thẳng.

Lời giải:

a) Bảng trên được gọi là bảng theo dõi thời giàn làm bài tập của 30 học sinh

Dấu hiệu cần tìm hiểu ở đây là thời giàn làm bài tập của mỗi học sinh

b) Ta có bảng tần số sau:

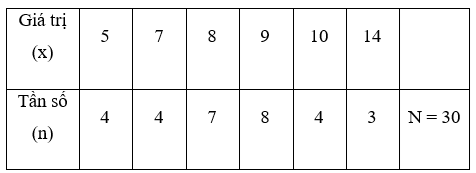
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 6)

Số trung bình cộng là: $\bar{X} = \frac{5.4 + 7.4 + 8.7 + 9.8 + 10.4 + 14.3}{30} = \frac{258}{30} = 8,6$

c) Mốt của dấu hiệu là M₀ = 9

Nhận xét:

+ Có 30 giá trị nhưng chỉ có 6 giá trị khác nhau

+ Thời gian làm bài ít nhất là 5 phút

+ Thời gian làm bài nhiều nhất là 14 phút

+ Số đông các bạn đềi hoàn thành bài tập khoảng từ 8 đến 10 phút

d) Biểu đồ đoạn thẳng

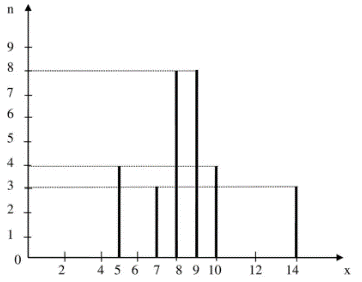
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 7)

Câu 28: Quan sát hình vẽ sau , biết $\hat{B A C} = \hat{A C D} = 30 °$ . Em hãy giải thích tại sao AB // CD.

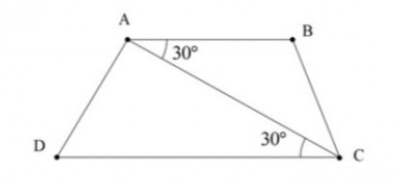
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 8)

Lời giải:

Ta có $\hat{B A C} = \hat{A C D} = 30 °$ (giả thiết)

Mà hai góc này ở vị trí so le trong

Suy ra AB // CD (dấu hiệu nhận biết)

Vậy AB // CD.

Câu 29: Cho x, y, z thỏa mãn x² + y² + z² ≤ 3.

Tìm giá trị nhỏ nhất của $P = \frac{1}{1 + x y} + \frac{1}{1 + y z} + \frac{1}{1 + x z}$ .

Lời giải:

Ta có (x + y + z)² ≥ 0

⇔ x² + y² + z² – 2xy – 2xz – 2yz ≥ 0

⇔ x² + y² + z² ≥ xy + yz + xz

Mà x² + y² + z² ≤ 3

Suy ra xy + yz + xz ≤ 3

Ta có P ≥ $\frac{{(1 + 1 + 1)}^{2}}{3 + (x y + y z + x z)}$

⇔ P ≥ $\frac{9}{3 + (x y + y z + x z)}$

Mà P ≥ $\frac{{(1 + 1 + 1)}^{2}}{3 + (x y + y z + x z)}$

Suy ra P ≥ $\frac{9}{3 + 3} = \frac{3}{2}$

Do đó P đạt giá trị nhỏ nhất bằng $\frac{3}{2}$ khi x = y = z = 1

Vậy giá trị nhỏ nhất của P bằng $\frac{3}{2}$ khi x = y = z = 1.

Câu 30: Cho x, y, z là số dương thỏa mãn x² + y² + z² = 3. Chứng minh rằng

$\frac{1}{1 + x y} + \frac{1}{1 + y z} + \frac{1}{1 + x z} \geq \frac{3}{2}$

Lời giải:

Áp dụng bất đẳng thức AM – GM có

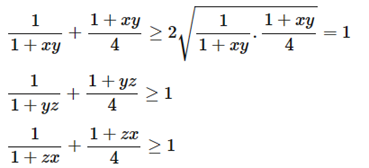
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 9)

Suy ra

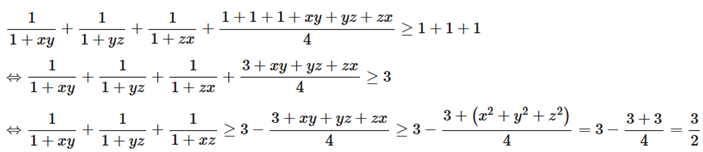
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 10)

Dấu “ = ” xảy ra khi x = y = z = 1

Vậy $\frac{1}{1 + x y} + \frac{1}{1 + y z} + \frac{1}{1 + x z} \geq \frac{3}{2}$ khi x² + y² + z² = 3.

Câu 31: Tìm tập xác định của hàm số:

a) y = cot(1 – x);

b) $y = x + \frac{1}{(\sin x + 1) \cot x}$ .

Lời giải:

a) ĐKXĐ: sin(1 – x) ≠ 0.

⇔ 1 – x ≠ kπ (k ∈ ℤ).

⇔ x ≠ 1 – kπ (k ∈ ℤ).

Vậy TXĐ: D = ℝ \ {1 – kπ | k ∈ ℤ).

b) ĐKXĐ: $\{\begin{cases} \sin x \neq 0 \\ \sin x + 1 \neq 0 \\ \cot x \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} \sin x \neq 0 \\ \sin x \neq - 1 \\ \cos x \neq 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} x \neq k π \\ x \neq - \frac{π}{2} + k 2 π \\ x \neq \frac{π}{2} + k π \end{cases} (k \in ℤ)$ .

$\Leftrightarrow x \neq \frac{k π}{2} (k \in ℤ)$ .

Vậy TXĐ: $D = ℝ \ \{\frac{k π}{2} | k \in ℤ\}$ .

Câu 32: Tính A = sin²2° + sin²4° + sin²6° + … + sin²84° + sin²86° + sin²88°.

A. 20;

B. 22;

C. 24;

D. 23.

Lời giải:

Đáp án đúng là: B

Ta có A = sin²2° + sin²4° + sin²6° + … + sin²84° + sin²86° + sin²88°.

= (sin²2° + sin²88°) + (sin²4° + sin²86°) + (sin²6° + sin²84°) + … + (sin²44° + sin²46°)

= (sin²2° + cos²2°) + (sin²4° + cos²4°) + (sin²6° + cos²6°) + … + (sin²44° + cos²44°)

= 1 + 1 + 1 + … + 1 (22 số 1)

= 22.

Vậy ta chọn phương án B.

Câu 33: Tính giá trị biểu thức A = sin²1° + sin²2° + … + sin²88° + sin²89° + sin²90°.

A. 46;

B. $\frac{93}{2}$ ;

C. $\frac{91}{2}$ ;

D. 45.

Lời giải:

Đáp án đúng là: C

Ta có A = sin²1° + sin²2° + … + sin²88° + sin²89° + sin²90°.

= (sin²1° + sin²89°) + (sin²2° + sin²88°) + … + (sin²44° + sin²46°) + sin²45° + sin²90°.

= (sin²1° + cos²1°) + (sin²2° + cos²2°) + … + (sin²44° + cos²44°) + sin²45° + sin²90°.

= $= \underset{44 s o 1}{\underset{⏟}{1 + 1 + ... + 1}} + \frac{1}{2} + 1 = 44.1 + \frac{3}{2} = \frac{91}{2}$ .

Vậy ta chọn phương án C.

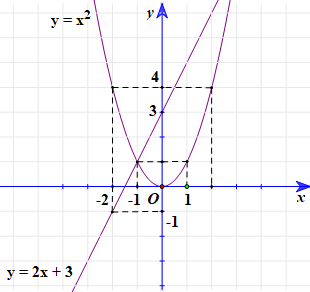
Câu 34: Vẽ đồ thị hai hàm số trên cùng hệ trục tọa độ y = x² và y = 2x + 3.

Lời giải:

Bảng giá trị của hàm số y = x²:

x	–2	–1	0	1	2
y	4	1	0	1	4

Bảng giá trị của hàm số y = 2x + 3:

x	–2	–1	0
y	–1	1	3

Đồ thị:

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 11)

Câu 35:

a) Vẽ đồ thị hàm số y = –x² (P) và hàm số y = –2x – 3 (D) trên cùng hệ tọa độ.

b) Tìm tọa độ giao điểm của (P) và (D).

c) Gọi giao điểm (P) và (D) là A. Tính độ dài từ A đến B(5; –7).

Lời giải:

a) Bảng giá trị của hàm số y = –x²:

x	–2	–1	0	1	2
y	–4	–1	0	–1	–4

Bảng giá trị của hàm số y = –2x – 3:

x	–2	–1	0
y	1	–1	–3

Đồ thị:

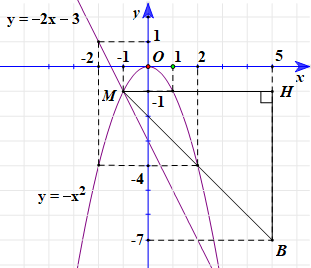
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 12)

b) Phương trình hoành độ giao điểm của (P) và (D): –x² = –2x – 3

⇔ x² – 2x – 3 = 0

⇔ (x – 3)(x + 1) = 0

⇔ x = 3 hoặc x = –1.

Với x = 3, ta có: y = –3² = –9.

Với x = –1, ta có: y = –(–1)² = –1.

Vậy giao điểm của (P) và (D) là M(–1; –1), N(3; –9).

c) Trường hợp 1: A ≡ M(–1; –1).

Gọi H là giao điểm của hai đường thẳng x = 5 và y = –1.

Suy ra tọa độ H(5; –1).

Ta có: MH = 5 + 1 = 6, BH = 7 – 1 = 6.

Tam giác MBH vuông tại H: MB² = MH² + BH² (Định lí Pytago).

= 6² + 6² = 72.

Suy ra $M B = 6 \sqrt{2}$ .

Trường hợp 2: A ≡ N(3; –9).

Ta thực hiện tương tự trường hợp 1, ta được: $N B = 2 \sqrt{2}$ .

Vậy độ dài từ A đến B(5; –7) lần lượt là $6 \sqrt{2}$ (khi A(–1; –1)) và $2 \sqrt{2}$ (khi A(3; –9)).

Câu 36: Trong hình 97, biết diện tích miền gạch sọc là 86 cm². Tính diện tích hình tròn.

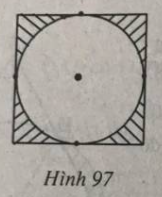
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 13)

Lời giải:

Gọi R là bán kính hình tròn.

Suy ra cạnh hình vuông là 2R.

Diện tích hình vuông là: S_hv = 4R².

Diện tích hình tròn là: S_tròn = π.R².

Theo đề, ta có S_sọc = 86.

⇔ S_hv – S_tròn = 86

⇔ 4R² – π.R² = 86

⇔ R².(4 – π) = 86

$\Leftrightarrow R^{2} = \frac{86}{4 - π}$

Suy ra $R = \sqrt{\frac{86}{4 - π}}$ (cm).

Vậy diện tích hình tròn là: $π . \frac{86}{4 - π} \approx 314,74 (c m^{2})$ .

Câu 37: Cho hình vuông ABCD cạnh a. Tính $|\vec{A D} + 3 \vec{A B}|$ theo a.

A. $a \sqrt{10}$ ;

B. $2 a \sqrt{2}$ ;

C. $2 a \sqrt{3}$ ;

D. 3a.

Lời giải:

Đặt $P = |\vec{A D} + 3 \vec{A B}|$ .

Suy ra $P^{2} = A D^{2} + 9 A B^{2} + 6. \vec{A D} . \vec{A B} = A D^{2} + 9 A B^{2} + 6. \vec{0}$ (vì AD ⊥ AB).

= AD² + 9AB² = a² + 9a² = 10a².

Suy ra $P = a \sqrt{10}$ .

Vậy ta chọn phương án A.

Câu 38: Tam giác ABC có AB = 3, AC = 6, $\hat{B A C} = 60 °$ . Tính độ dài đường cao HA của tam giác.

Lời giải:

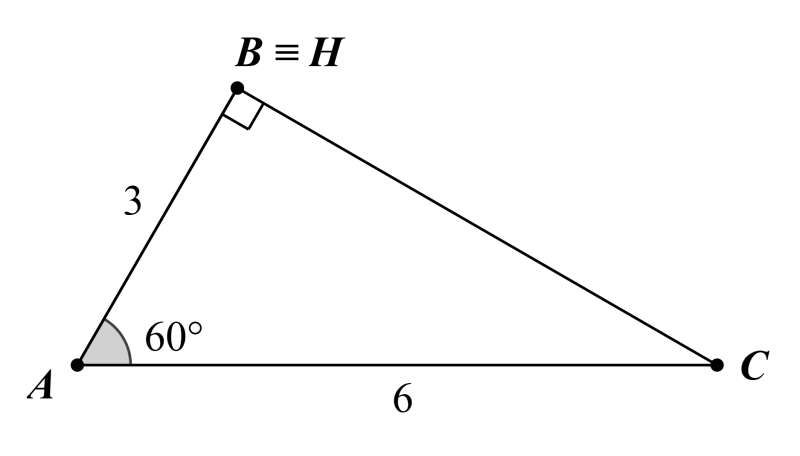
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 14)

BC² = AB² + AC² – 2.AB.AC.cos $\hat{B A C}$ .

= 9 + 36 – 2.3.6.cos60°

= 27.

Suy ra $B C = 3 \sqrt{3}$ .

$\cos \hat{A B C} = \frac{A B^{2} + B C^{2} - A C^{2}}{2. A B . B C} = \frac{9 + 27 - 36}{2.3.3 \sqrt{3}} = 0$ .

Suy ra $\hat{A B C} = 90 °$ .

Do đó tam giác ABC vuông tại A.

Vì vậy B ≡ H.

Vậy AH = AB = 3.

Câu 39: Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của DA, BC. Tính góc giữa hai đường thẳng AB và CD biết AB = CD = 2a; $M N = a \sqrt{3}$ .

A. 30°;

B. 45°;

C. 60°;

D. 90°.

Lời giải:

Đáp án đúng là: C

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 15)

Ta có $\vec{M N} = \frac{1}{2} (\vec{M A} + \vec{A B} + \vec{B N}) + \frac{1}{2} (\vec{M D} + \vec{D C} + \vec{C N})$

$= \frac{1}{2} (\vec{M A} + \vec{M D}) + \frac{1}{2} (\vec{B N} + \vec{C N}) + \frac{1}{2} (\vec{A B} + \vec{D C})$ (M, N lần lượt là trung điểm của DA, BC).

$= \frac{1}{2} . \vec{0} + \frac{1}{2} . \vec{0} + \frac{1}{2} (\vec{A B} + \vec{D C}) = \frac{1}{2} (\vec{A B} + \vec{D C})$ .

Suy ra $M N^{2} = \frac{1}{4} (A B^{2} + D C^{2} + 2 \vec{A B} . \vec{D C})$

$\Leftrightarrow 3 a^{2} = \frac{1}{4} (4 a^{2} + 4 a^{2} + 2 \vec{A B} . \vec{D C})$

$\Leftrightarrow \vec{A B} . \vec{D C} = 2 a^{2}$ .

Ta có $\cos (\vec{A B}, \vec{D C}) = \frac{\vec{A B} . \vec{D C}}{A B . D C} = \frac{2 a^{2}}{2 a .2 a} = \frac{1}{2}$ .

Suy ra $(\vec{A B}, \vec{D C}) = 60 °$ .

Vậy góc giữa hai đường thẳng AB và CD bằng 60°.

Do đó ta chọn phương án C.

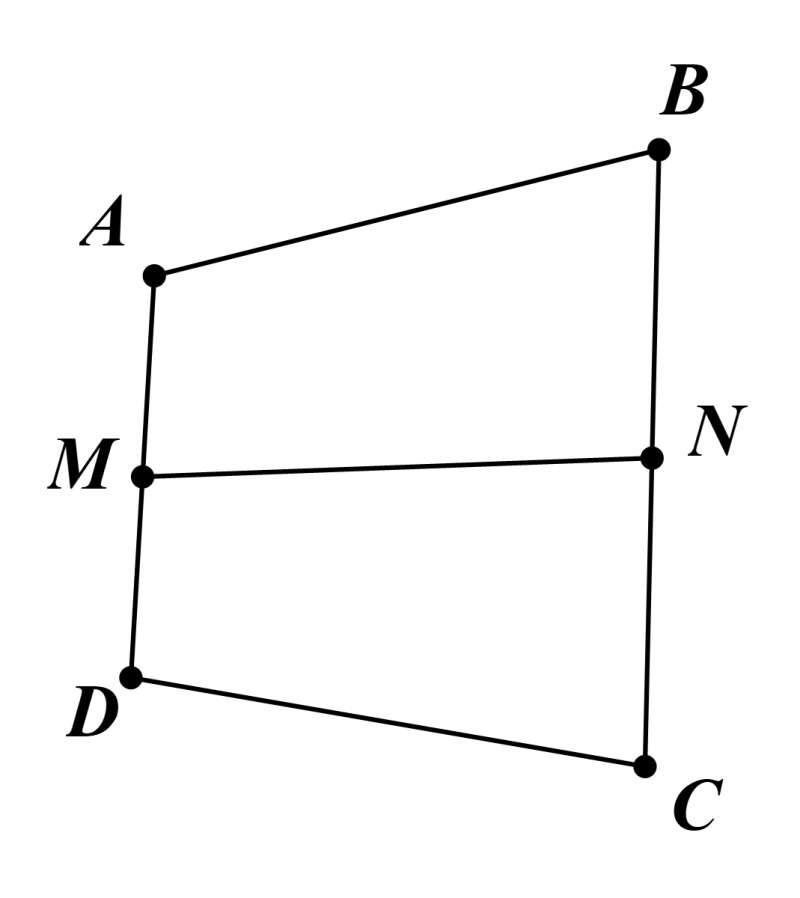
Câu 40: Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AD, BC.

a) Chứng minh $\vec{M N} = \frac{1}{2} (\vec{A B} + \vec{D C})$ .

b) Xác định điểm O sao cho $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{0}$ .

Lời giải:

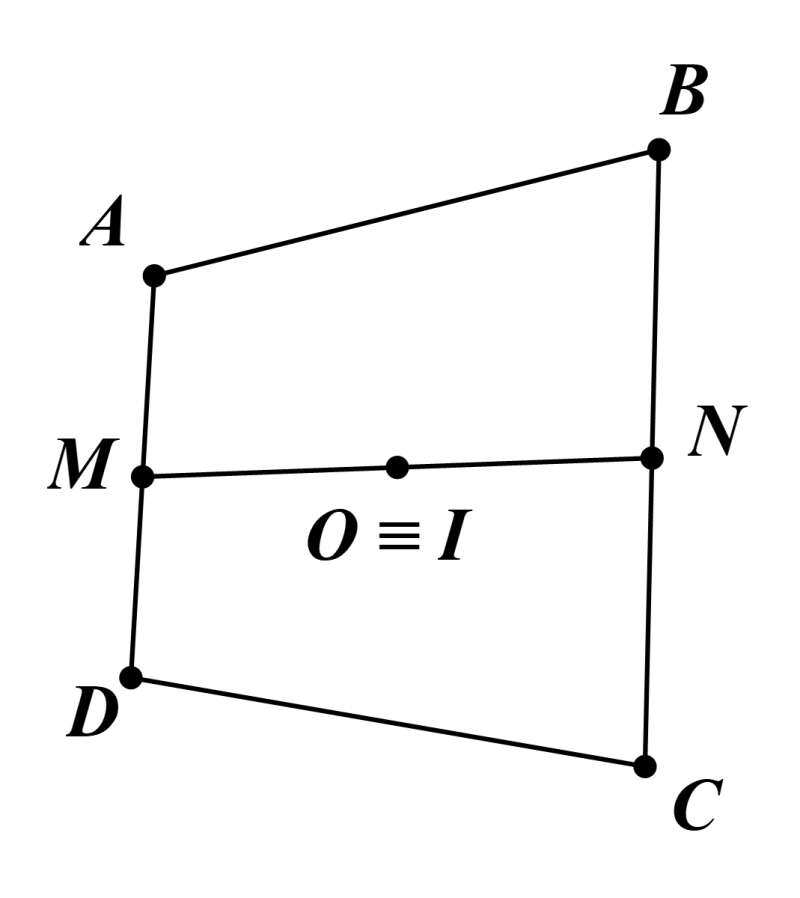
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 16)

a) Ta có $V T = \vec{M N} = \frac{1}{2} (\vec{M A} + \vec{A B} + \vec{B N}) + \frac{1}{2} (\vec{M D} + \vec{D C} + \vec{C N})$

$= \frac{1}{2} (\vec{M A} + \vec{M D}) + \frac{1}{2} (\vec{B N} + \vec{C N}) + \frac{1}{2} (\vec{A B} + \vec{D C})$ (M, N lần lượt là trung điểm của DA, BC).

$= \frac{1}{2} . \vec{0} + \frac{1}{2} . \vec{0} + \frac{1}{2} (\vec{A B} + \vec{D C}) = \frac{1}{2} (\vec{A B} + \vec{D C}) = V P$ .

Vậy ta có điều phải chứng minh.

b) Ta có $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{O A} + \vec{O D} + \vec{O C} + \vec{O B}$

$= 2 \vec{O M} + 2 \vec{O N} = 2 (\vec{O M} + \vec{O N}) = 4 \vec{O I}$ , với I là trung điểm MN.

Khi đó $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{0} \Leftrightarrow \vec{O I} = \vec{0}$ .

Tức là, O ≡ I.

Vậy O ≡ I thỏa mãn yêu cầu bài toán.

Câu 41: Tính $\sqrt{6 - 2 \sqrt{5}}$ .

Lời giải:

Ta có $\sqrt{6 - 2 \sqrt{5}} = \sqrt{5 - 2 \sqrt{5} + 1} = \sqrt{{(\sqrt{5} - 1)}^{2}} = |\sqrt{5} - 1| = \sqrt{5} - 1$ .

Câu 42: Rút gọn biểu thức $\sqrt{6 + 2 \sqrt{5}} - \sqrt{6 - 2 \sqrt{5}}$ .

Lời giải:

Ta có

$\sqrt{6 + 2 \sqrt{5}} - \sqrt{6 - 2 \sqrt{5}} = \sqrt{5 + 2 \sqrt{5} + 1} - \sqrt{5 - 2 \sqrt{5} + 1} = \sqrt{{(\sqrt{5} + 1)}^{2}} - \sqrt{{(\sqrt{5} - 1)}^{2}} = |\sqrt{5} + 1| - |\sqrt{5} - 1| = \sqrt{5} + 1 - (\sqrt{5} - 1) = 2$

Câu 43: Phân tích nhân tử x³ – y³.

Lời giải:

Ta có x³ – y³ = (x – y)(x² + xy + y²).

Câu 44: Khai triển hằng đẳng thức: x³ + y³.

Lời giải:

Ta có x³ + y³ = (x + y)(x² – xy + y²).

Câu 45: Tìm tất cả các giá trị nguyên của tham số m ∈ [–3; 5] để hàm số y = (2m – 3)x + 5m – 1 nghịch biến trên ℝ.

Lời giải:

Hàm số nghịch biến trên ℝ ⇔ 2m – 3 < 0 $\Leftrightarrow m < \frac{3}{2}$ .

Ta có m ∈ [–3; 5].

Suy ra m ∈ {–3; –2; –1; 0; 1}.

Vậy m ∈ {–3; –2; –1; 0; 1} thỏa mãn yêu cầu bài toán.

Câu 46: Tìm tất cả các giá trị thực của tham số m để hàm số y = (m – 1)x⁴ – 2(m – 3)x² + 1 không có cực đại?

A. 1 ≤ m ≤ 3;

B. m ≤ 1;

C. m ≥ 1;

D. 1 < m ≤ 3.

Lời giải:

Đáp án đúng là: A

Trường hợp 1: m = 1.

Khi đó y = 4x² + 1 ≥ 1 > 0, ∀x ∈ ℝ.

Cho y’ = 0 ⇔ 8x = 0 ⇔ x = 0.

Vì vậy hàm số không có cực đại, chỉ có cực tiểu x = 0 khi m = 1.

Trường hợp 2: m ≠ 1.

Hàm số đã cho không có cực đại $\Leftrightarrow \{\begin{cases} m - 1 > 0 \\ - 2 (m - 3) \geq 0 \end{cases} \Leftrightarrow \{\begin{cases} m > 1 \\ m \leq 3 \end{cases} \Leftrightarrow 1 < m \leq 3$ .

Vậy 1 ≤ m ≤ 3 thỏa mãn yêu cầu bài toán.

Do đó ta chọn phương án A.

Câu 47: Tìm tất cả các giá trị thực của tham số m để hàm số $y = (m + 1) x^{4} - m x^{2} + \frac{3}{2}$ chỉ có cực tiểu mà không có cực đại.

A. m < –1;

B. –1 < m < 0;

C. m > 1;

D. –1 ≤ m < 0.

Lời giải:

Đáp án đúng là: D

Trường hợp 1: m = –1.

Khi đó $y = x^{2} + \frac{3}{2} \geq \frac{3}{2} > 0, \forall x \in ℝ$ .

Cho y’ = 0 ⇔ 2x = 0 ⇔ x = 0.

Vì vậy hàm số không có cực đại, chỉ có cực tiểu x = 0 khi m = –1.

Trường hợp 2: m ≠ –1.

Hàm số đã cho không có cực đại $\Leftrightarrow \{\begin{cases} m + 1 > 0 \\ - m \geq 0 \end{cases} \Leftrightarrow \{\begin{cases} m > - 1 \\ m \leq 0 \end{cases} \Leftrightarrow - 1 < m \leq 0$ .

Vậy –1 ≤ m ≤ 0 thỏa mãn yêu cầu bài toán.

Do đó ta chọn phương án D.

Câu 48: Cho hai hàm số y = –2x² (P) và y = 3x + m – 1 (d). Tìm m để (d) cắt (P) tại hai điểm nằm bên trái trục tung.

Lời giải:

Phương trình hoành độ giao điểm của (P) và (d): 2x² + 3x + m – 1 = 0 (1)

∆ = 3² – 4.2.(m – 1) = 9 – 8m + 8 = 17 – 8m.

Ta có (P) cắt (d) tại hai điểm nằm bên trái trục tung.

⇔ Phương trình (1) có 2 nghiệm âm phân biệt.

$\Leftrightarrow \{\begin{cases} Δ > 0 \\ S < 0 \\ P > 0 \end{cases} \Leftrightarrow \{\begin{cases} 17 - 8 m > 0 \\ \frac{- 3}{2} < 0 (d u n g) \\ \frac{m - 1}{2} > 0 \end{cases} \Leftrightarrow \{\begin{cases} m < \frac{17}{8} \\ m > 1 \end{cases} \Leftrightarrow 1 < m < \frac{17}{8}$

Vậy $1 < m < \frac{17}{8}$ thỏa mãn yêu cầu bài toán.

Câu 49: Tìm m để giao điểm của d: y = 12x + 5 – m; d’: y = 3x + m + 3 nằm bên trái trục tung.

A. m < 1;

B. m = 1;

C. m > 1;

D. m > 2.

Lời giải:

Phương trình hoành độ giao điểm của d và d’: 12x + 5 – m = 3x + m + 3.

⇔ 9x = 2m – 2.

$\Leftrightarrow x = \frac{2 m - 2}{9}$ .

Do d cắt d’ tại điểm nằm bên trái trục tung nên ta có x < 0.

$\Leftrightarrow \frac{2 m - 2}{9} < 0 \Leftrightarrow 2 m - 2 < 0 \Leftrightarrow m < 1$ .

Vậy m < 1 thỏa mãn yêu cầu bài toán.

Do đó ta chọn phương án A.

Câu 50: Cho 4 điểm A, B, C, D bất kì. Gọi E, F lần lượt là trung điểm AB, CD, O là trung điểm EF. Chứng minh $4 \vec{A O} = \vec{A B} + \vec{A C} + \vec{A D}$ .

Lời giải:

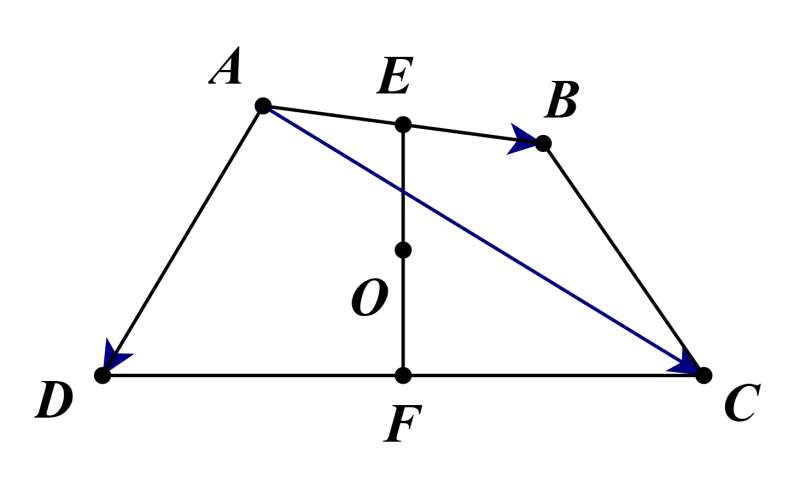
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 17)

Ta có $V P = \vec{A O} + \vec{O B} + \vec{A O} + \vec{O C} + \vec{A O} + \vec{O D}$

$= 3 \vec{A O} + \vec{O E} + \vec{E B} + 2 \vec{O F} = 3 \vec{A O} + \vec{O E} + \vec{A E} + 2 \vec{O F}$ (do E, F lần lượt là trung điểm của AB, CD).

$= 3 \vec{A O} + \vec{O E} + \vec{A O} + \vec{O E} + 2 \vec{O F} = 4 \vec{A O} + 2 (\vec{O E} + \vec{O F})$

(do O là trung điểm EF).

Vậy ta có điều phải chứng minh.

Câu 51: Cho 4 điểm A, B, C, D bất kì. Gọi E, F lần lượt là trung điểm AB, CD. O là trung điểm EF. Chứng minh rằng $\vec{A D} + \vec{B C} = 2 \vec{E F}$ .

Lời giải:

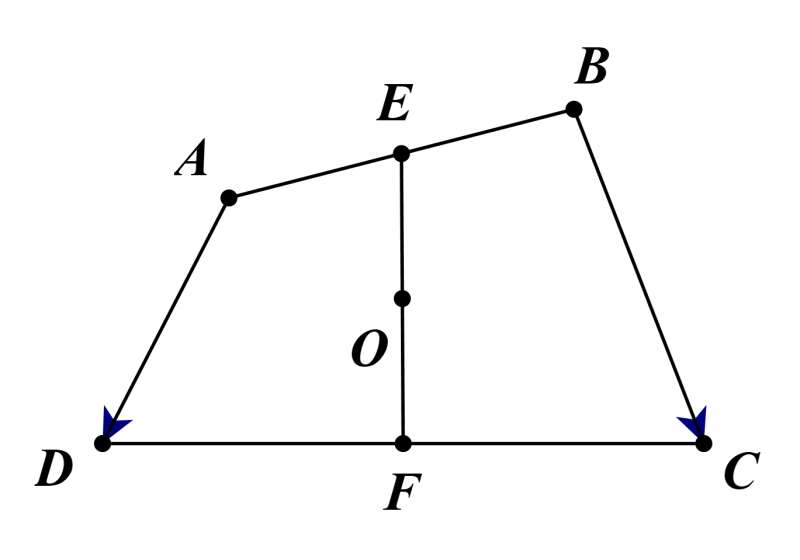
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) (ảnh 18)

Ta có $V T = \vec{A E} + \vec{E F} + \vec{F D} + \vec{B E} + \vec{E F} + \vec{F C}$

$= 2 \vec{E F} + (\vec{A E} + \vec{B E}) + (\vec{F D} + \vec{F C})$ (do E, F lần lượt là trung điểm của AB, CD).

$= 2 \vec{E F} + \vec{0} + \vec{0} = 2 \vec{E F} = V P$ .

Vậy ta có điều phải chứng minh.

Câu 52:

a) Tìm x, biết: x(x + 3) – x² + 9 = 0.

b) Thực hiện phép chia: A = 2x² + 3x – 2 cho B = 2x – 1.

Lời giải:

a) x(x + 3) – x² + 9 = 0

⇔ x(x + 3) – (x² – 9) = 0

⇔ x(x + 3) – (x + 3)(x – 3) = 0

⇔ (x + 3)(x – x + 3) = 0

⇔ (x + 3).3 = 0

⇔ x + 3 = 0

⇔ x = –3.

Vậy x = –3.

$\begin{matrix} 2 x^{2} & + & 3 x & - & 2 \\ \bar{} & 2 x^{2} & - & x \\ 4 x & - & 2 \\ 4 x & - & 2 \\ 0 \end{matrix} \begin{matrix} 2 x - 1 \\ x + 2 \end{matrix}$

Vậy A : B = x + 2.

Câu 53: Tìm x, biết: 2x(x – 3) + x² – 9 = 0.

Lời giải:

2x(x – 3) + x² – 9 = 0

⇔ 2x(x – 3) + (x – 3)(x + 3) = 0

⇔ (x – 3)(2x + x + 3) = 0

⇔ (x – 3)(3x + 3) = 0

⇔ x – 3 = 0 hoặc 3x + 3 = 0

⇔ x = 3 hoặc x = –1.

Vậy x = 3 hoặc x = –1.

Câu 54: Biểu thức $\sqrt{\frac{1}{a}}$ có nghĩa khi nào?

Lời giải:

ĐKXĐ: $\{\begin{cases} \frac{1}{a} \geq 0 \\ a \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} a \geq 0 \\ a \neq 0 \end{cases} \Leftrightarrow a > 0$ .

Vậy biểu thức $\sqrt{\frac{1}{a}}$ có nghĩa khi và chỉ khi a > 0.

Câu 55: Giải phương trình $x - 2 \sqrt{x - 3} = 3$ .

Lời giải:

$x - 2 \sqrt{x - 3} = 3$ (điều kiện: x ≥ 3).

$\Leftrightarrow x - 3 - 2 \sqrt{x - 3} = 0 \Leftrightarrow \sqrt{x - 3} (\sqrt{x - 3} - 2) = 0 \Leftrightarrow [\begin{array}{l} \sqrt{x - 3} = 0 \\ \sqrt{x - 3} = 2 \end{array} \Leftrightarrow [\begin{array}{l} x - 3 = 0 \\ x - 3 = 4 \end{array}$