Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 24) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Vẽ đồ thị hàm số y = –x2 (P) và hàm số y = –2x – 3 (D) trên cùng hệ tọa độ.
Câu 35:
a) Vẽ đồ thị hàm số y = –x2 (P) và hàm số y = –2x – 3 (D) trên cùng hệ tọa độ.
b) Tìm tọa độ giao điểm của (P) và (D).
c) Gọi giao điểm (P) và (D) là A. Tính độ dài từ A đến B(5; –7).
Lời giải:
a) Bảng giá trị của hàm số y = –x2:
|
x |
–2 |
–1 |
0 |
1 |
2 |
|
y |
–4 |
–1 |
0 |
–1 |
–4 |
Bảng giá trị của hàm số y = –2x – 3:
|
x |
–2 |
–1 |
0 |
|
y |
1 |
–1 |
–3 |
Đồ thị:
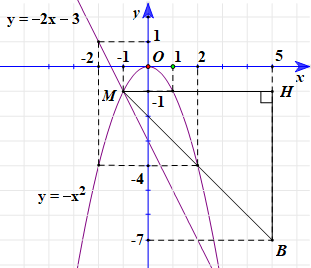
b) Phương trình hoành độ giao điểm của (P) và (D): –x2 = –2x – 3
⇔ x2 – 2x – 3 = 0
⇔ (x – 3)(x + 1) = 0
⇔ x = 3 hoặc x = –1.
Với x = 3, ta có: y = –32 = –9.
Với x = –1, ta có: y = –(–1)2 = –1.
Vậy giao điểm của (P) và (D) là M(–1; –1), N(3; –9).
c) Trường hợp 1: A ≡ M(–1; –1).
Gọi H là giao điểm của hai đường thẳng x = 5 và y = –1.
Suy ra tọa độ H(5; –1).
Ta có: MH = 5 + 1 = 6, BH = 7 – 1 = 6.
Tam giác MBH vuông tại H: MB2 = MH2 + BH2 (Định lí Pytago).
= 62 + 62 = 72.
Suy ra .
Trường hợp 2: A ≡ N(3; –9).
Ta thực hiện tương tự trường hợp 1, ta được: .
Vậy độ dài từ A đến B(5; –7) lần lượt là (khi A(–1; –1)) và (khi A(3; –9)).
Bài viết cùng bài học:




