Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 8) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 8)
Lời giải:
Xét tam giác ABC có:
Vậy có 6 vecto khác vecto không có điểm đầu; điểm cuối là các đỉnh của tam giác.
Câu 2: Cho n thuộc ℕ. Chứng minh n2 + n + 1 không chia hết cho 4 và không chia hết cho 5.
Lời giải:
+) Ta có: n2 + n + 1 = n(n + 1) + 1
Thấy n(n + 1) là hai số tự nhiên liên tiếp nên sẽ bao gồm một số chẵn và một số lẻ. Do đó, n(n + 1) ⋮ 2
⇒ n(n + 1) + 1 không chia hết cho 2
⇒ n2 + n + 1 không chia hết cho 2
⇒ n2 + n + 1 không chia hết cho 4.
+) Tích 2 số tự nhiên liên tiếp có chữ số tận cùng là 0; 2; 6
⇒ n(n + 1) có chữ số tận cùng là 0; 2; 6
⇒ n(n + 1) + 1 có chữ số tận cùng là 1; 3; 7 hay n2 + n + 1 có chữ số tận cùng là 1; 3; 7
⇒ n2 + n + 1 không chia hết cho 5
Lời giải:
Tổng học sinh ít nhất giỏi 1 môn học là:
40 – 22 =18
Theo bài ra, có 10 học sinh giỏi toán, 15 bạn học sinh giỏi lí
Do đó, tổng số học chỉ giỏi toán, học sinh chỉ giỏi lí và học sinh vừa giỏi toán vừa giỏi lí là 10 + 15 = 25 (học sinh)
Vậy số học sinh giỏi toán và lí là : 25 – 18 = 7 (học sinh)
Câu 4: Xác định a, b, c biết parabol y = ax2 + bx + c đi qua 3 điểm A(–1; –3), B(4; 42), C(–2; 0).
Lời giải:
Parabol y = ax2 + bx + c đi qua điểm A(–1; –3) nên ta có:
–3 = a.(–1)2 + b.(–1) + c ⇒ a – b + c = –3
Parabol y = ax2 + bx + c đi qua điểm B(4; 42) nên ta có:
42 = a.42 + b.4 + c ⇒ 16a + 4b + c = 42
Parabol y = ax2 + bx + c đi qua điểm C(–2; 0) nên ta có:
0 = a.(–2)2 + b.(–2) + c ⇒ 4a – 2b + c = 0
Từ đó, ta có hệ phương trình:
Vậy a = 2, b = 3, c = –2
Câu 5: Xác định a, b, c biết parabol y = ax2 + bx + c đi qua 3 điểm A( 0; –1), B(1; –1), C(–1; 1).
Lời giải:
Parabol y = ax2 + bx + c đi qua điểm A( 0; –1) nên ta có:
–1 = a.02 + b.0 + c ⇒ c = –1
Parabol y = ax2 + bx + c đi qua điểm B(1; –1) nên ta có:
–1 = a.12 + b.1 + c ⇒ a + b – 1 = –1 ⇒ a + b = 0
Parabol y = ax2 + bx + c đi qua điểm C(–1; 1) nên ta có:
1 = a.(–1)2 + b.(–1) + c ⇒ a – b – 1 = 1 ⇒ a – b = 2
Từ đó, ta có hệ phương trình:
Vậy a = 1, b = –1, c = –1.
Câu 6: Phương trình có bao nhiêu nghiệm ?
Lời giải:
(x ≠ 0)
(*)
Do –1 ≤ sinx ≤ 1 nên
Nếu x = x0 là nghiệm của phương trình (*) thì x = –x0 cũng là nghiệm của phương trình (*)
Vẽ đồ thị của hàm số y = sinx và
Ta thấy:
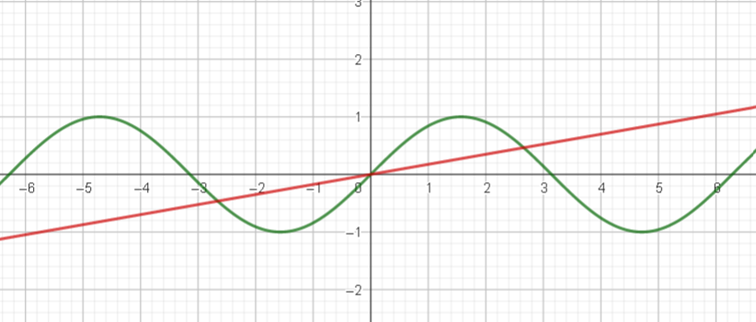
Trên đoạn ta thấy phương trình (*) có ba nghiệm phân biệt, trong đó có 1 nghiệm x = 0 (loại).
Vậy phương trình có hai nghiệm.
Câu 7: Cho tam giác ABC cân tại A đường cao AH và BK cắt nhau tại I. Chứng minh:
a) Đường tròn đường kính AI đi qua K.
b) HK là tiếp tuyến của đường tròn đường kính AI.
Lời giải:
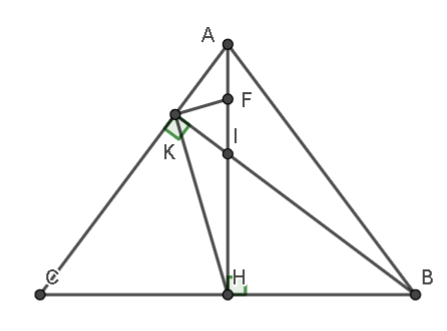
a)
Gọi F là trung điểm của AI
Do BK là đường cao của tam giác ABC nên
Xét tam giác AKI vuông tại K có:
KF là đường trung tuyến ứng với cạnh huyền.
Do đó, KF = FI = FA
Vậy K nằm trên đường tròn đường kính AI.
b)
Xét tam giác AKF có: FA =FK (cmt)
Do đó, AKF cân tại F
(1)
Do AH là đường cao của tam giác ABC cân tại A nên ta AH cũng là đường trung tuyến hay H là trung điểm của BC
Xét tam giác CKB vuông tại K có:
KH là đường trung tuyến ứng với cạnh huyền
⇒ KH = CH = BH
Xét tam giác CHK có: CH = HK (cmt)
Do đó, tam giác CHK cân tại H (2)
Xét tam giác AHC vuông tại H có: (3)
Từ (1), (2) và (3) ta có:
Do đó, HK vuông góc với FK mà FK là bán kính của đường tròn đường kính AI.
Vậy HK là tiếp tuyến của đường tròn đường kính AI.
Câu 8: Giải phương trình lượng giác: 2sinx.(1 + cos2x) + sin2x = 1 + 2cosx
Lời giải:
2sinx(1 + cos2x) + sin2x = 1 + 2cosx
⇔ 2sinx.(1 + 2cos2x – 1) + 2sinxcosx = 1 + 2cosx
⇔ 2sinx.2cos2x + 2sinxcosx = 1 + 2cosx
⇔ 2sinxcosx(2cosx + 1) = 1 + 2cosx
⇔ 2sinxcosx(2cosx + 1) – (1 + 2cosx) = 0
⇔ (2cosx + 1)(2sinxcosx – 1) = 0
⇔ (2cosx + 1).(sin2x – 1) = 0
a) BE vuông góc với AF.
b) BM vuông góc với EF.
c) Các đường thẳng BM, AF và CE đồng quy.
Lời giải:
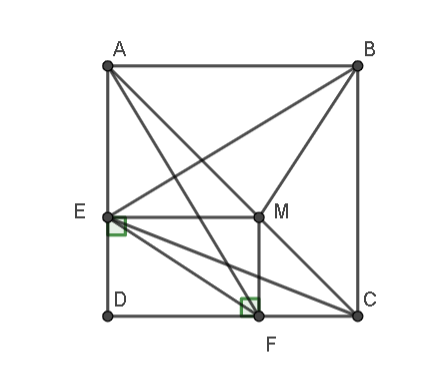
a)
Gọi giao của BM với EF là I, FM và AB là K
Vì tam giác ADF bằng tam giác BAE (cạnh huyền–cạnh góc vuông)
Nên
⇒
Do đó, AF vuông góc với EB
b)
Vì ABCD là hình vuông nên AC là phân giác của
Xét tứ giác AKME có
AK // ME
MK //AE
AM là phân giác của
Do đó, AKME là hình vuông
⇒ MK = ME và KB = MF
Do đó, tam giác KMB bằng tam giác MEF
Mà
Do đó, BM vuông góc với EF
c)
Xét tam giác BEF có:
BM,AF là các đường cao
nên BM cắt AF tại trực tâm của tam giác
Do đó, M là trực tâm
Vậy BM,AF,CE đồng quy
Lời giải:
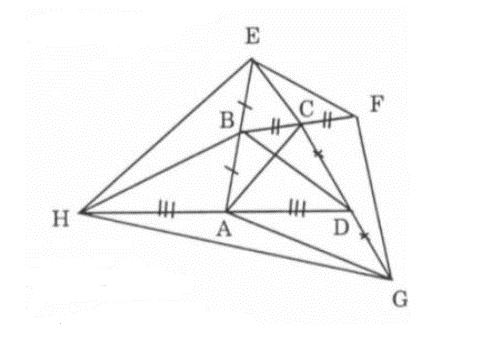
Ta có BA là trung tuyến của tam giác HBD nên diện tích tam giác BAH bằng diện tích tam giác BAD.
HB là trung tuyến của tam giác HEA nên
Do đó
Chứng minh tương tự có:
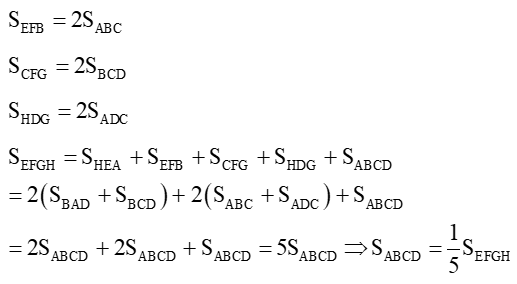
Câu 11: Phân tích đa thức thành nhân tử: a3 – 3a + 3b – b3
Lời giải:
a3 – 3a + 3b – b3
= (a3 – b3) – (3a – 3b)
= (a – b)(a2 + ab + b2) – 3(a – b)
= (a – b)(a2 + ab + b2 – 3)
Lời giải:
Vậy x ∈ {4; –1}
Lời giải:
|x–1| = 2 (*)
TH1: x – 1 ≥ 0 ⇒ x ≥ 1
(*) ⇔ x – 1 = 2
⇔ x = 3
TH2: x – 1 < 0 ⇒ x < 1
(*) ⇔ x – 1 = –2
⇔ x = –1
Câu 14: Cho hình thoi ABCD cạnh bằng 1 và có . Tính độ dài cạnh AC.
Lời giải:
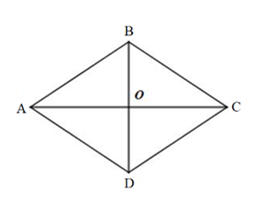
Do ABCD là hình thoi, có nên góc
Theo định lí hàm cosin, ta có
AC2 = AB2 + BC2 – 2AB.BC.cos = 12 + 12 – 2.1.1.cos = 3
Câu 15: Cho hình thoi ABCD có cạnh bằng a, . Tính
Lời giải:
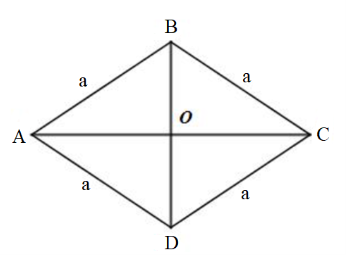
Ta có:
Gọi O la giao điểm hai đường chéo AC và BD.
Tam giác ABD đều nên BD = a, OD =
Xét tam giác OCD vuông tại O có:
Áp dụng định lý Py–ta–go ta có:
Câu 16: Tìm x biết: (x + 60%) : 16 = 5%
Lời giải:
(x + 60%) : 16 = 5%
(x + 0,6) : 16 = 0,05
x + 0,6 = 0,05.16
x + 0,6 = 0,8
x = 0,8 – 0,6
x = 0,2
Vậy x = 0,2
Lời giải:
Lời giải:
(A ∪ B) ∪ C = { 0;1;2;3;4;6;9;8}
A ∪ (B ∪ C) = { 0;1;2;3;4;6;9;8}
⇒ (A ∪ B) ∪ C = A ∪ (B ∪ C)
Lời giải:
Gọi A là tập hợp HS giỏi toán ( 10 bạn)
Gọi B là tập hợp HS giỏi lý ( 15 bạn)
A ∩ B là tập hợp các HS vừa giỏi toán vừa giỏi lý. Còn lại 22 bạn ko giỏi môn nào nên ta có: 40 – 22 = 18 (1)
Giao của 2 tập hợp A và B là: 15+10=25 (2)
Từ (1) và (2) suy ra:
A ∪ B : 25 – 18 = 7
Câu 20: Nghiệm của phương trình: sin4x + cos5x = 0 là
Lời giải:
Ta có:
sin4x + cos4x = 0 ⟺ cos5x = –sin4x
Vậy phương trình đã cho có nghiệm là hoặc .
Lời giải:
Do giá mỗi quyển sách tăng thêm 1000 đồng so với dự định, nên khi bạn An mua 5 quyển sách thì số tiền đã tăng lên thêm: 1000. 5 = 5000 (đồng) so với dự định. Do giá mỗi cây bút giảm đi 500 đồng so với dự định nên khi mua 2 cây bút thì bạn An được giảm:
2. 500 = 1000 (đồng) so với dự định
Do số tiền tăng lên (5000 đồng) nhiều hơn số tiền được giảm (1000 đồng) so với dự định, nên để mua 5 quyển tập và 2 cây bút như dự định ban đầu thì bạn An còn thiếu số tiền là: 5000 – 1000 = 4000 (đồng)
Vậy để mua 5 quyển tập và 2 cây bút như dự định ban đầu thì bạn An còn thiếu số tiền là: 4000 đồng.
Lời giải:
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
với
⟺ 2x + 1 = (x + 2)(2x – 1)
⟺ 2 + x – 3 = 0
⟺ x = 1 hoặc
Hai nghiệm này đều thỏa mãn điều kiện.
Với x = 1 ta có y = 3 suy ra A(1; 3)
Vậy ta có suy ra
Vậy đường thẳng d cắt đồ thị (C) tại hai điểm là A và B có tọa độ là: A(1;3) và
Câu 23: Giải phương trình: (3x – 5)(2x – 1) – (x + 2)(6x – 1) = 0.
Lời giải:
(3x – 5)(2x – 1) – (x + 2)(6x – 1) = 0
Lời giải:
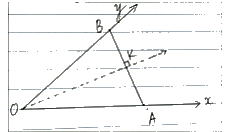
Ta có: ΔOAB cân tại O (vì OA = OB)
Mà OK là phân giác, do đó OK cũng là đường trung tuyến của tam giác OAB.
Nên K là trung điểm của AB ⇒ KA = KB.
Câu 25: Cho x, y, z > 0 và x + 2y + 3z ≥ 10. Tìm min P .
Lời giải:
P
Dấu = xảy ra khi .
Câu 26: Cho hệ phương trình: . Chứng minh phương trình luôn có nghiệm duy nhất với mọi m.
Lời giải:
Ta có:
Với m = 0 hệ phương trình tương đương: .
Hệ phương trình có nghiệm duy nhất
Với m ≠ 0,
Do > 0
Nên .
Với mỗi giá trị của m chỉ cho 1 cặp nghiệm (x, y).
Vậy với mọi giá trị của m hệ phương trình luôn có nghiệm duy nhất.
Lời giải:
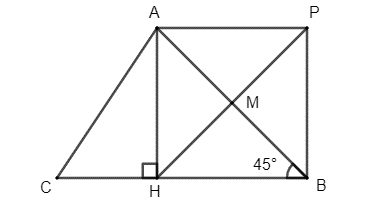
Xét tứ giác AHBP có
M là trung điểm chung của AB và HP
AH = HB (∆AHB vuông cân tại H)
Do đó: AHBP là hình vuông.
Câu 28: Cho 2 điểm A(3; –5); B(1; 0). Tìm tọa độ điểm C sao cho . Tính điểm D đối xứng qua C.
Lời giải:
C(x; y)
A(3; –5); B(1; 0)
Điểm D đối xứng với A qua D A là trung điểm AC .
Câu 29: Cho tam giác đều ABC cạnh a, M là trung điểm BC. Tính độ dài .
Lời giải: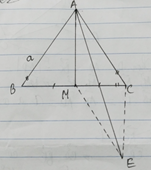
(hình vẽ)
⇒
⇒ .
Câu 30: Tìm giá trị lớn nhất của trên đoạn .
Lời giải:
⇒
⇒ Max = .
Câu 31: Tìm giá trị lớn nhất của hàm số trên đoạn .
Lời giải:
y(–1) = 1; y(1) = 3; = –1
⇒ Min = –1.
Câu 32: Chứng minh rằng với mọi giá trị của m thì phương trình luôn có nghiệm.
Lời giải:
Phương trình luôn có nghiệm (1)
Ta có: ∆1
Xét f(x) có:
⇒ f(x) > 0 ( m)
⇒ ∆1 > 0 m ⇒ (1) luôn có nghiệm với mọi m (đpcm).
Câu 33: Tìm tập nghiệm của phương trình .
Lời giải:
Điều kiện:
⟺
Thử lại ta thấy cả x = 0 và x = 2 đều thỏa mãn phương trình
Lời giải:
Điều kiện xác định:
Phương trình ⟺
⟺
Vậy tập nghiệm của phương trình đã cho là: .
Lời giải: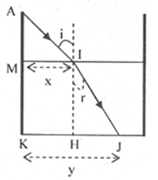
Theo hình vẽ ta có:
⟹ HJ = 51,25 cm
Độ dài vệt sáng dưới đáy bể là:
y = x + HJ = 85,9 cm
Lời giải:
xG yG
Vậy G(–1; –3).
Do điểm I thuộc trục hoành nên I(x; 0)
Do điểm I thuộc đường thằng BG nên
Suy ra
Vậy .
Lời giải:
Câu 38: Phân tích đa thức sau thành nhân tử: .
Lời giải:
Ta có: .
Câu 39: Cho tam giác ABC có trọng tâm G và độ dài 3 cạnh AB, BC, CA lần lượt là 15, 18, 27.
a) Tính diện tích và bán kính đường tròn nội tiếp tam giác ABC.
b) Tính diện tích tam giác GBC.
Lời giải:
a) Nửa chu vi của tam giác ABC là:
Áp dụng công thức Heron ta tính được diện tích tam giác ABC là:
Mặt khác S = pr (r là bán kính đường tròn nội tiếp tam giác ABC).
Suy ra
Vậy diện tích tam giá ABC là ( đơn vị diện tích), bán kính đường tròn nội tiếp tam giác ABC là (đơn vị độ dài).
b) Do G là trọng tâm tam giác ABC nên G chia tam giác ABC thành 3 tam giác GAB, GAC, GBC có diện tích bằng nhau.
Suy ra SGBC
Vậy diện tích của tam giác GBC: ( đơn vị diện tích).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.