Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 8) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho tam giác ABC cân tại A đường cao AH và BK cắt nhau tại I. Chứng minh:
Câu 7: Cho tam giác ABC cân tại A đường cao AH và BK cắt nhau tại I. Chứng minh:
a) Đường tròn đường kính AI đi qua K.
b) HK là tiếp tuyến của đường tròn đường kính AI.
Lời giải:
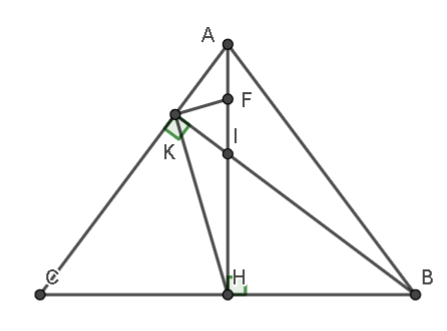
a)
Gọi F là trung điểm của AI
Do BK là đường cao của tam giác ABC nên
Xét tam giác AKI vuông tại K có:
KF là đường trung tuyến ứng với cạnh huyền.
Do đó, KF = FI = FA
Vậy K nằm trên đường tròn đường kính AI.
b)
Xét tam giác AKF có: FA =FK (cmt)
Do đó, AKF cân tại F
(1)
Do AH là đường cao của tam giác ABC cân tại A nên ta AH cũng là đường trung tuyến hay H là trung điểm của BC
Xét tam giác CKB vuông tại K có:
KH là đường trung tuyến ứng với cạnh huyền
⇒ KH = CH = BH
Xét tam giác CHK có: CH = HK (cmt)
Do đó, tam giác CHK cân tại H (2)
Xét tam giác AHC vuông tại H có: (3)
Từ (1), (2) và (3) ta có:
Do đó, HK vuông góc với FK mà FK là bán kính của đường tròn đường kính AI.
Vậy HK là tiếp tuyến của đường tròn đường kính AI.
Xem thêm các bài giải Tổng hợp kiến thức môn Toán hay, chi tiết khác:
Câu 2: Cho n thuộc ℕ. Chứng minh n2 + n + 1 không chia hết cho 4 và không chia hết cho 5.
Câu 4: Xác định a, b, c biết parabol y = ax2 + bx + c đi qua 3 điểm A(–1; –3), B(4; 42), C(–2; 0).
Câu 5: Xác định a, b, c biết parabol y = ax2 + bx + c đi qua 3 điểm A( 0; –1), B(1; –1), C(–1; 1).
Câu 6: Phương trình y có bao nhiêu nghiệm ?
Câu 7: Cho tam giác ABC cân tại A đường cao AH và BK cắt nhau tại I. Chứng minh:
Câu 8: Giải phương trình lượng giác: 2sinx.(1 + cos2x) + sin2x = 1 + 2cosx
Câu 11: Phân tích đa thức thành nhân tử: a3 – 3a + 3b – b3
Câu 14: Cho hình thoi ABCD cạnh bằng 1 và có . Tính độ dài cạnh AC.
Bài viết cùng bài học:




