Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 72)

Ngọc Nguyễn Ngày: 22-10-2023 Tổng hợp kiến thức

323

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 72) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 72)

Câu 1: Có 6 quả cầu xanh đánh số từ 1 đến 6, 5 quả cầu đỏ đánh số từ 1 đến 5 và 7 quả màu vàng đánh số từ 1 đến 7. Hỏi có bao nhiêu cách lấy ra 3 quả cầu vừa khác màu vừa khác số?

Lời giải:

Để lấy ra ba quả cầu vừa khác màu vừa khác số ta phải thực hiện qua ba giai đoạn:

• Chọn một quả cầu đỏ.

• Chọn một quả cầu xanh.

• Chọn một quả cầu vàng.

• Chọn quả cầu đỏ có 5 cách chọn.

• Chọn quả cầu xanh có 5 cách chọn (trừ quả cầu được đánh số trùng với quả cầu đỏ).

• Chọn quả cầu vàng có 5 cách chọn (trừ hai quả cầu được đánh số trùng với quả cầu đỏ và quả cầu xanh).

Theo quy tắc nhân ta được 5. 5. 5 = 125 cách lấy ra ba quả cầu vừa khác màu vừa khác số.

Vậy có 125 cách lấy ra ba quả cầu vừa khác màu vừa khác số.

Câu 2: Tính thể tích của khối bát diện đều cạnh a.

Lời giải:

Thể tích khối bát diện đều là:

$V = 2 V_{1} = 2. \frac{a^{3}}{3 \sqrt{2}} = \frac{a^{3} \sqrt{2}}{3}$

Vậy thể tích của khối bát diện đều cạnh a là $\frac{a^{3} \sqrt{2}}{3}$ .

Câu 3: Tìm x, biết: x² – 8x + 16 = 0.

Lời giải:

x² – 8x + 16 = 0

⇔ (x – 4)² = 0

⇔ x – 4 = 0

⇔ x = 4

Vậy x = 4.

Câu 4: Cho các hàm số: y = 2x − 2 và y = (m + 1)x − m² – m (m ≠ −1). Tìm m để đồ thị hai hàm số trên là các đường thẳng song song.

Lời giải:

Để hai đồ thị hàm số trên song song thì:

$\{\begin{matrix} m + 1 = 2 \\ m^{2} + m \neq 2 \end{matrix} \Leftrightarrow \{\begin{matrix} m = 1 \\ (m - 1) (m + 2) \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} m = 1 \\ m \neq 1 \\ m \neq - 2 \end{matrix}$ (vô lý)

Vậy không tồn tại m để 2 đường thẳng trên song song.

Câu 5: Tìm m để hai đường thẳng (d): y = 3x + 1 và (d′): y = (m−1)x − 2m song song với nhau.

Lời giải:

Để d // d’ thì: $\{\begin{matrix} m - 1 = 3 \\ - 2 m \neq 1 \end{matrix} \Leftrightarrow \{\begin{matrix} m = 4 \\ m \neq \frac{- 1}{2} \end{matrix}$

Vậy m = 4 thì d // d’.

Câu 6: Cho hàm số y = –x³ + 3x + 2. Tìm hai điểm trên đồ thị hàm số sao cho chúng đối xứng nhau qua điểm M(–1; 3).

Lời giải:

Gọi A(x₀; y₀) và B là điểm đối xứng với A qua điểm M(–1; 3)

Suy ra M là trung điểm của AB nên B(–2 – x₀; 6 – y₀).

Do A và B thuộc đồ thị hàm số (C) nên:

$\{\begin{cases} y_{0} = - x_{0}^{3} + 3 x_{0} + 2 (1) \\ 6 - y_{0} = - {(- 2 + x_{0})}^{3} + 3 (- 2 - x_{0}) + 2 (2) \end{cases}$

Từ (1) và (2) lấy vế cộng vế ta được:

6 = –x₀³ + 3x₀ + 2 – (–2 – x₀)³ + 3(–2 – x₀) + 2

⇔ 6 = –x₀³ + 3x₀ + 2 + 8 + 12x₀ + 6x₀² + x₀³ – 6 – 3x₀ + 2

⇔ 6x₀² + 12x₀ + 6 = 0

⇔ x₀ = –1 nên y₀ = 0.

Vậy 2 điểm cần tìm là: (–1; 0) và (–1; 6).

Câu 7: Trong mặt phẳng tọa độ Oxy cho hai đồ thị hàm số y = x – 5m và y’ = 3x – m². Tìm m để 2 đường thẳng cắt nhau tại 1 điểm có hoành độ bằng –3.

Lời giải:

Ta có: y = x – 5m (1)

y’ = 3x – m² (2)

Để (1) và (2) cắt nhau tại một điểm thì y = y’

⇔ x – 5m = 3x – m²

⇔ m² – 5m = 2x

Mà hai đồ thị cắt nhau tại điểm có hoành độ bằng –3 nên:

m² – 5m = 2. (–3)

⇔ m² – 5m + 6 = 0

⇔ m²– 2m – 3m + 6 = 0

⇔ m(m – 2) – 3(m – 2) = 0

⇔ (m – 2)(m – 3) = 0

$\Leftrightarrow [\begin{matrix} m - 2 = 0 \\ m - 3 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} m = 2 \\ m = 3 \end{matrix}$

Vậy giá trị m thỏa mãn là m = 2 hoặc m = 3.

Câu 8: Trong mặt phẳng tọa độ Oxy cho hàm số bậc nhất y = (2k – 1)x + 3 – k (k là hệ số) có đồ thị là đường thẳng (d). Tìm giá trị của k để đồ thị hàm số song song với đường thẳng (m): y = 0,5x – 3.

Lời giải:

Để đường thẳng (d) // (m) thì:

$\{\begin{matrix} 2 k - 1 = 0,5 \\ 3 - k \neq - 3 \end{matrix} \Leftrightarrow \{\begin{matrix} k = \frac{3}{4} (t m) \\ k \neq 6 \end{matrix}$

Vậy giá trị k thỏa mãn là $k = \frac{3}{4}$ .

Câu 9: Trong kì thi học sinh giỏi tỉnh có 4 bạn Phương, Dương, Hiếu, Hằng tham gia. Được hỏi quê mỗi người ở đâu ta nhận được các câu trả lời sau:

Phương: Dương ở Thăng Long còn tôi ở Quang Trung.

Dương : Tôi cũng ở Quang Trung còn Hiếu ở Thăng Long.

Hiếu : Không, tôi ở Phúc Thành còn Hằng ở Hiệp Hoà.

Hằng : Trong các câu trả lời trên đều có 1 phần đúng 1 phần sai.

Hỏi quê của Dương ở đâu?

Lời giải:

Vì trong mỗi câu trả lời đều có 1 phần đúng và 1 phần sai nên có các trường hợp:

• Giả sử Dương ở Thăng Long là đúng thì Phương ở Quang Trung là sai.

Suy ra Dương ở Quang Trung là sai. Vậy Hiếu ở Thăng Long là đúng.

Điều này vô lý vì Dương và Hiếu cùng ở Thăng Long.

• Giả sử Dương ở Thăng Long là sai, suy ra Phương ở Quang Trung và do đó Dương ở Quang Trung là sai.

Suy ra Hiếu ở Thăng Long. Vậy Hiếu ở Phúc Thành là sai. Suy ra Hằng ở Hiệp Hòa.

Còn lại Dương ở Phúc Thành.

Vậy Dương ở Phúc Thành.

Câu 10: Cho parabol (P): y = x² và hai điểm A(0; 1); B(1; 3). Viết phương trình đường thẳng AB.

Lời giải:

Gọi phương trình AB có dạng y = ax + b

Khi đó $\{\begin{matrix} 0 a + b = 1 \\ a + b = 3 \end{matrix} \Leftrightarrow \{\begin{matrix} a = 2 \\ b = 1 \end{matrix}$

Vậy phương trình đường thẳng AB là: y = 2x + 1.

Câu 11: Cho parabol (P): y = x² và hai điểm A(0; 1); B(1; 3). Viết phương trình đường thẳng d song song với AB và tiếp xúc với (P).

Lời giải:

Đường thẳng d song song với AB có dạng: y = 2x + b (b ≠ 1)

Phương trình hoành độ giao điểm của d và (P) là:

x² = 2x + b ⇔ x² − 2x – b = 0 (∗)

Ta có Δ’ = 1 + b.

Đường thẳng d tiếp xúc với (P) ⇔ Δ′ = 0 ⇔ 1 + b = 0 ⇔ b = −1 (tm)

Vậy đường thẳng d song song với AB và tiếp xúc với (P) là: y = 2x – 1.

Câu 12: Tìm x: x : 0,25 + x × 11 = 24

Lời giải:

x : 0,25 + x × 11 = 24

x × 4 + x × 11 = 24

x × (4 + 11) = 24

x × 15 = 24

x = 24 : 15

x = 1,6

Vậy x = 1,6.

Câu 13: Tìm x: x × 9,8 – x : 0,25 = 18,096

Lời giải:

x × 9,8 – x : 0,25 = 18,096

x × 9,8 – x × 4 = 18,096

x × (9,8 – 4) = 18,096

x × 4,8 = 18,096

x = 18,096 : 4,8

x = 3,77

Câu 14: Tìm x: 0,16 : (x : 3,5) = 2,8

Lời giải:

0,16 : (x : 3,5) = 2,8

0,16 : x × 3,5 = 2,8

0,56 : x = 2,8

x = 0,56 : 2,8

x = 0,2

Vậy x = 0,2

Câu 15: Giải phương trình: x⁴ + 2x² – 3 = 0

Lời giải:

x⁴ + 2x² – 3 = 0

⇔ (x⁴ + 2x²+ 1) – 4 = 0

⇔ (x² + 1)² − 2² = 0

⇔ (x² + 1 − 2)(x² + 1 + 2) = 0

⇔ (x²– 1)(x²+ 3) = 0

Vì x²≥ 0 nên x²+ 3 > 0 với mọi x

Do đó x²– 1 = 0

⇔ x²= 1

⇔ x = ± 1

Vậy tập nghiệm của phương trình đã cho là S = {−1; 1}.

Câu 16: Phân tích đa thức thành nhân tử: x³ – x²y – xy² + y³.

Lời giải:

Ta có: x³ – x²y – xy² + y³

= x²(x – y) – y²(x – y)

= (x² – y²)(x – y)

= (x – y)²(x + y)

Câu 17: Phân tích đa thức thành nhân tử: –6x² – 9xy + 15y².

Lời giải:

–6x² – 9xy + 15y²

= –(6x² + 9xy – 15y²)

= –(6x² – 6xy + 15xy – 15y²)

= –[6x(x – y) + 15y(x – y)]

= –[(x – y)(6x + 15y)]

Câu 18: Cùng một lúc hai xe xuất phát từ hai địa điểm A và B cách nhau 80 km. Chúng chuyển động thẳng đều và cùng chiều từ A đến B. Xe thứ nhất khởi hành từ A với vận tốc 30 km/h. Xe thứ hai đi từ B với vận tốc 40 km/h. Tính khoảng cách giữa hai xe sau 1 giờ kể từ lúc xuất phát.

Lời giải:

Sau 1 giờ, xe thứ nhất đi được quãng đường là:

30. 1 = 30 (km)

Sau 1 giờ, xe thứ hai đi được quãng đường là:

40. 1 = 40 (km)

Sau 1 giờ, hai xe cách nhau quãng đường là:

80 – 30 – 40 = 10 (km)

Đáp số: 10 km

Câu 19: Cùng một lúc hai xe xuất phát từ hai địa điểm A và B cách nhau 160 km. Chúng chuyển động thẳng đều và cùng chiều từ A đến B. Xe thứ nhất khởi hành từ A với vận tốc 30 km/h. Xe thứ hai đi từ B với vận tốc 40 km/h. Sau khi xuất phát 1 giờ, xe thứ nhất tăng tốc và đạt tối đa vận tốc 50 km/h. Xác định thời điểm hai xe gặp nhau.

Lời giải:

Sau 1 giờ, xe thứ nhất đi được quãng đường là:

30. 1 = 30 (km)

Sau 1 giờ, xe thứ hai đi được quãng đường là:

40. 1 = 40 (km)

Sau 1 giờ, hai xe cách nhau quãng đường là:

160 – 30 – 40 = 90 (km)

Sau khi xe thứ nhất tăng tốc, thời gian hai xe gặp nhau là:

90 : (50 + 40) = 1 (giờ)

Tổng thời gian 2 xe đã đi là:

1 + 1 = 2 (giờ)

Đáp số: 2 giờ.

Câu 20: Đĩa xích của xe đạp có 80 răng, đĩa líp có 40 răng. Tính số truyền i và cho biết chi tiết nào quay nhanh hơn?

Lời giải:

Áp dụng công thức ta có: $i = \frac{Ζ_{1}}{Ζ_{2}}$

Vậy tỉ số truyền ở đây là: $i = \frac{Ζ_{1}}{Ζ_{2}} = \frac{80}{20} = 4$ .

Câu 21: Tích: 1 × 2 × 3 × 4 × 5 × … × 45 × 46 có tận cùng bao nhiêu chữ số 0?

Lời giải:

Các thừa số tròn chục trong tích trên là: 10; 20; 30 và 40

⇒ Các thừa số trên tạo ra 4 chữ số 0.

Các thừa số có tận cùng là chữ số 5 trong tích trên là: 5; 15; 25; 35 và 45

trong đó, 25 = 5 × 5.

Mỗi thừa số có tận cùng là chữ số 5 nhân với một thừa số chẵn sẽ tạo ra một số có tận cùng là chữ số 0.

Do đó các thừa số trên tạo ra 6 chữ số 0.

Tích 1 × 2 × 3 × 4 × 5 × … × 45 × 46 có tận cùng số chữ số 0 là:

4 + 6 = 10 (chữ số)

Vậy tích 1 × 2 × 3 × 4 × 5 × … × 45 × 46 có tận cùng 10 chữ số 0.

Câu 22: Tích 2 × 11 × 6 × 14 × 15 × 17 × 18 × 25 × 45 có tận cùng bao nhiêu chữ số 0?

Lời giải:

Các thừa số có tận cùng là chữ số 5 trong tích trên là: 15; 25 và 45

trong đó, 25 = 5 × 5.

Mỗi thừa số có tận cùng là chữ số 5 nhân với một thừa số chẵn sẽ tạo ra một số có tận cùng là chữ số 0.

Do đó các thừa số trên tạo ra 4 chữ số 0

Vậy 2 × 11 × 6 × 14 × 15 × 17 × 18 × 25 × 45 có tận 4 chữ số 0.

Câu 23: Xác định hàm số y = ax²+ bx + c có giá trị nhỏ nhất bằng 2 khi x = 1 và nhận giá trị bằng 3 khi x = 2.

Lời giải:

Hàm số y = ax²+ bx + c có giá trị nhỏ nhất bằng 2 khi x = 1 nên ta có:

$\frac{- b}{2 a} = 1 \Leftrightarrow 2 a + b = 0$ (1)

2 = a. 1² + b. 1 + c ⇔ a + b + c = 2 (2)

Hàm số y = ax²+ bx + c nhận giá trị bằng 3 khi x = 2 nên ta có:

4a + 2b + c = 3 (3)

Từ (1), (2) và (3) ta có: $\{\begin{matrix} 2 a + b = 0 \\ a + b + c = 2 \\ 4 a + 2 b + c = 3 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} a = 1 \\ b = - 2 \\ c = 3 \end{matrix}$

Vậy hàm số cần tìm là: y = x² – 2x + 3.

Câu 24: Cho đa thức p(x) = ax² + bx + c (với a, b, c là các số hữu tỉ). Biết P(0), P(1), P(2) là các số nguyên. Chứng minh P(x) có giá trị nguyên với mọi x nguyên.

Lời giải:

P(0) = c mà P(0) nguyên

⇒ c nguyên

P(1) = a + b + c mà P(1) nguyên

⇒ a + b + c nguyên mà c nguyên

⇒ a + b nguyên

P(2) = 4a + 2b + c mà P(2) nguyên

⇒ 4a + 2b + c nguyên mà c nguyên

⇒ 4a + 2b nguyên hay 2a + b nguyên

⇒ 2a + b − (a + b) nguyên

⇒ a nguyên mà a + b nguyên

⇒ b nguyên

Do đó a, b, c nguyên

Vậy P(x) có giá trị nguyên với mọi x nguyên.

Câu 25: Cho nửa đường tròn đường kính AB cố định. C là một điểm trên nửa đường tròn, trên dây AC kéo dài lấy điểm D sao cho CD = CB. Trên tia CA lấy điểm E sao cho CE = CB. Tìm quỹ tích các điểm E khi C chạy trên nửa đường tròn đã cho.

Lời giải:

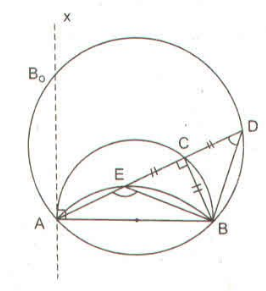
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 72) (ảnh 1)

Ta có: AB cố định

$\hat{A E B} = 135 °$ (góc ngoài của tam giác BCE vuông cân)

Suy ra khi C chuyển động trên nửa đường tròn đường kính AB cố định thì E chuyển động trên cung chứa góc 135° dựng trên đoạn thẳng AB cố định.

Vậy quỹ tích các điểm E khi C chạy trên nửa đường tròn đường kính AB là cung chứa góc 135° dựng trên đoạn thẳng AB cố định.

Câu 26: Có 6 quả cầu xanh đánh số từ 1 đến 6, 5 quả cầu đỏ đánh số từ 1 đến 5 và 7 quả màu vàng đánh số từ 1 đến 7. Hỏi có bao nhiêu cách lấy ra 3 quả cầu vừa khác màu vừa khác số?

Lời giải:

Để lấy ra ba quả cầu vừa khác màu vừa khác số ta phải thực hiện qua ba giai đoạn:

+ Chọn một quả cầu đỏ

+ Chọn một quả cầu xanh

+ Chọn một quả cầu vàng

Chọn quả cầu đỏ có 5 cách chọn

Chọn quả cầu xanh có 5 cách chọn (trừ quả cầu được đánh số trùng với quả cầu đỏ)

Chọn quả cầu vàng có 5 cách chọn (trừ hai quả cầu được đánh số trùng với quả cầu đỏ và quả cầu xanh)

Theo quy tắc nhân ta được 5. 5. 5 = 125 cách lấy ra ba quả cầu vừa khác màu vừa khác số

Vậy có 125 cách lấy ra ba quả cầu vừa khác màu vừa khác số.

Câu 27: Cho các hàm số: y = 2x − 2 và y = (m + 1)x −?² – ? (m ≠ −1). Tìm m để đồ thị hai hàm số trên là các đường thẳng song song.

Lời giải:

Để hai đồ thị hàm số trên song song thì:

Vậy không tồn tại m để 2 đường thẳng trên song song.

Câu 28: Tìm m để hai đường thẳng (d): y = 3x + 1 và (d′): y = (m−1)x − 2m song song với nhau.

Lời giải:

Để d // d’ thì: $\{\begin{matrix} m - 1 = 3 \\ - 2 m \neq 1 \end{matrix} \Leftrightarrow \{\begin{matrix} m = 4 \\ m \neq \frac{- 1}{2} \end{matrix}$

Vậy m = 4 thì d // d’.

Câu 29: Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AB. Gọi M, N lần lượt là trung điểm của SA, SB. Chứng minh MN // (SCD).

Lời giải:

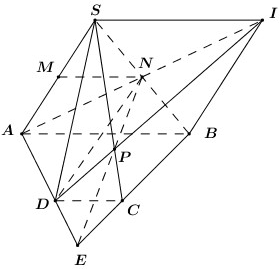
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 72) (ảnh 2)

Ta có: MN là đường trung bình của ΔSAB

⇒ MN // AB

Mà AB // CD (vì ABCD là hình thang)

⇒ MN // CD

Lại có: CD Ì (SCD)

⇒ MN // (SCD)

Vậy MN // (SCD).

Câu 30: Hình thoi ABCD có diện tích 20 cm² và đường chéo AC bằng 10 cm. Tính độ dài đường chéo BD.

Lời giải:

Độ dài đường chéo BD là:

$B D = \frac{2. 20}{10} = 4 (c m)$

Đáp số: 4 cm.

Câu 31: Tìm giá trị nhỏ nhất của biểu thức: A = |x – 3| + |x – 5| + |x – 7|.

Lời giải:

Ta có: A = |x – 3| + |x – 5| + |x – 7|

= |x – 3| + |x – 5| + |7 – x| ≥ | x − 3 + 7 − x | + | x − 5 |

= | 4 | + | x − 5 |

= 4 + | x − 5 |

Do |x – 5| ≥ 0 nên 4 + |x – 5| ≥ 4

⇒ |x – 3| + |x – 5| + |7 – x| ≥ 4

Dấu "=" xảy ra khi |x – 5| = 0

⇔ x − 5 = 0

⇔ x = 5

Vậy GTNN của A = 4 khi x = 5.

Câu 32: Tìm giá trị nhỏ nhất của biểu thức: M = |x + 5| + |x + 2| + |x – 7| + |x – 8|

Lời giải:

Ta có: M = |x + 5| + |x + 2| + |x – 7| + |x – 8| ≤ |−x + 8 – x – 2 + x + 5 + x + 7| = 18

Dấu bằng xảy ra khi −5 ≤ x ≤ −2.

Vậy M có giá trị nhỏ nhất là 18 khi −5 ≤ x ≤ −2.

Câu 33: Tìm n ∈ ℤ, biết: (n – 3) + (n – 2) + (n – 1) + … + 10 + 11 = 11.

Lời giải:

(n – 3) + (n – 2) + (n – 1) + … + 10 + 11 = 11

⇔ (n – 3) + (n – 2) + (n – 1) + … + 10 = 0

Gọi số các số hạng từ n – 3 đến 10 là x (số hạng) ( $x \in ℕ^{*}$ )

Ta có:

[10 + (n – 3)]. x : 2 = 0

⇔ (n + 7). x = 0

Vì x > 0 nên n + 7 = 0 ⇔ n = –7 (tmđk)

Vậy n = –7.

Câu 34: Tìm n ∈ ℤ, biết: (n + 1) + (n + 2) + (n + 3) + (n + 4) = 90

Lời giải:

(n + 1) + (n + 2) + (n + 3) + (n + 4) = 90

⇔ 4n + 10 = 90

⇔ 4n = 80

⇔ n = 20

Vậy n = 20.

Câu 35: Giải phương trình: (x + 3) – |x + 7| = 0.

Lời giải:

(x + 3) – |x + 7| = 0

⇔ x + 3 = |x + 7|

• Với x ≥ –3, ta có: x + 3 = x + 7

⇔ 0 = 4 (vô lí)

• Với x < –3, ta có: x + 3 = –x – 7

⇔ 2x = –10

⇔ x = –5 (TMĐK)

Vậy nghiệm của phương trình đã cho là x = –5.

Câu 36: Tìm x, y ∈ ℕ sao cho: xy + x + y = 17.

Lời giải:

xy + x + y = 17

⇔ x(y + 1) + (y + 1) = 18

⇔ (x + 1)(y + 1) = 18

Do x, y ∈ ℕ nên ta có bảng:

x + 1	1	2	3	6	9	18
y + 1	18	9	6	3	2	1
x	0	1	2	5	8	17
y	17	8	5	2	1	0

Vậy các cặp số (x, y) là (0; 17), (1; 8), (2; 5), (5; 2), (8; 1), (17; 0).

Câu 37: Tìm tất cả các số nguyên dương n để n² + 31 là số chính phương.

Lời giải:

Đặt n² + 31 = a² (a ∈ ℕ)

⇔ a² – n²= 33

⇔ (a - n)(a + n) = 33 = 1. 31

Dễ thấy a – n < a + n nên ta có:

$\{\begin{matrix} a - n = 1 \\ a + n = 31 \end{matrix} \Leftrightarrow \{\begin{matrix} a = 16 \\ n = 15 \end{matrix}$

Vậy n = 15

Câu 38: Chứng minh rằng với mọi số nguyên x, y thì:

A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y⁴ là số chính phương.

Lời giải:

Ta có: A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y⁴

= (x² + 5xy + 4y²)( x² + 5xy + 6y²) + y⁴

Đặt x² + 5xy + 5y² = t (t ∈ ℕ)

A = (t – y²)(t + y²) + y⁴= t²– y⁴ + y⁴ = t²

Vậy A là số chính phương.

Câu 39: Chứng minh A = n(n + 1)(n + 2)(n + 3) + 1 là số chính phương với n là số tự nhiên.

Lời giải:

Ta có: A = n(n + 1)(n + 2)(n + 3) + 1 = (n² + 3n)(n² + 3n + 2) + 1

Đặt n² + 3n = t (t ∈ ℕ)

A = t(t + 2) + 1

= t²+ 2t + 1 = (t + 1)²

Vậy A là số chính phương.

Câu 40: Tìm số dư của phép chia 37,99 cho 16 nếu lấy đến 2 chữ số ở phần thập phân của thương.

Lời giải:

Ta có: 37,99 = 16 × 2,37 + 0,07

Vậy số dư của phép chia 37,99 cho 16 là 0,07.

Câu 41: Tìm số dư của phép chia 32,451 chia cho 24 nếu lấy đến 3 chữ số ở phần thập phân của thương.

Lời giải:

Ta có: 32,451 = 24 × 1,352 + 0,003

Vậy số dư của phép chia 32,451 chia cho 24 là 0,003.

Câu 42: Tìm số tự nhiên n sao cho n² + 2n + 12 là số chính phương.

Lời giải:

Đặt n² + 2n + 12 = k² $(k \in ℕ)$

⇔ n² + 2n + 1 + 11 = k²

⇔ (n + 1)² + 11 = k²

⇔ k²– (n + 1)² = 11

⇔ (k – n – 1)(k + n + 1) = 11 = 1. 11

Dễ thấy k + n + 1 > k – n – 1 nên ta có:

$\{\begin{matrix} k + n + 1 = 11 \\ k - n - 1 = 1 \end{matrix} \Leftrightarrow \{\begin{matrix} k + n = 10 \\ k - n = 2 \end{matrix} \Leftrightarrow \{\begin{matrix} k = 6 \\ n = 4 \end{matrix}$