Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 61)

Ngọc Nguyễn Ngày: 07-08-2023 Tổng hợp kiến thức

300

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 61) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 61)

Câu 1: Cho f(x) = −x² − 2(m − 1)x + 2m − 1.

Tìm m để bất phương trình f(x) > 0 đúng với mọi x thuộc (0; 1)

Lời giải:

f(x) = −x² − 2(m − 1)x + 2m − 1

Xét ∆’ = (m − 1)²− (−1)(2m − 1) = m² ≥ 0, ∀x ∈ℝ

• TH1: ∆’= 0 ⇒ m = 0

Khi đó f(x) = −x² + 2x − 1 = −(x − 1)² ≤ 0, ∀x ∈ℝ

Vậy với m = 0 không thỏa mãn yêu cầu bài toán

• TH2: ∆’ > 0 ⇒ m ≠ 0

Khi đó f(x) = 0 cho hai nghiệm a, b

Ta có BBT của f(x) = 0 như sau:

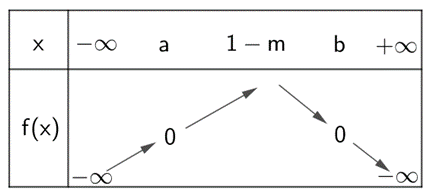
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 61) (ảnh 1)

Để f(x) > 0 đúng với mọi x thuộc (0; 1) thì:

$\{\begin{cases} f (0) \leq 0 \\ f (1) \geq 0 \end{cases} \Leftrightarrow \{\begin{cases} 2 m - 1 \leq 0 \\ 0 \geq 0 \end{cases} \Leftrightarrow m \leq \frac{1}{2}$

Vậy $m \leq \frac{1}{2}$ là giá trị thỏa mãn.

Câu 2: Tìm ba số, biết tổng thứ nhất và thứ hai bằng 182. Tổng của số thứ hai và thứ ba bằng 176, tổng của số thứ ba và số thứ nhất bằng 188.

Lời giải:

Tổng 3 số là:

(182+176+188): 2 = 273

Số thứ nhất là:

273 − 176 = 97

Số thứ 2 là:

182 − 97 = 85

Số thứ 3 là:

176 − 85 = 91

Đáp số: 97, 85 và 91.

Câu 3: Tổng của số thứ nhất và số thứ hai là 18,36;tổng của số thứ hai và số thứ ba là 21,64; tổng của số thứ ba và số thứ nhất là 20. Tính tổng của ba số đó?

Lời giải:

Tổng của 3 số là:

(18,36 + 21,64 + 20) : 2 = 30

Đáp số: 30.

Câu 4: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy và SA = a. Tính góc giữa đường thẳng SB và mặt phẳng đáy.

Lời giải:

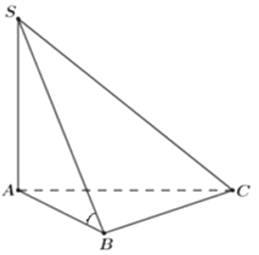
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 61) (ảnh 2)

SA vuông góc với mặt phẳng (ABC) nên góc giữa SB và mặt phẳng (ABC) là $\hat{S B A}$ .

Xét tam giác SBA vuông tại A ta có:

$\tan \hat{S B A} = \frac{S A}{A B} = \frac{a}{a} = 1 \Rightarrow \hat{S B A} = 45 °$ .

Câu 5: Cho B=3 + 3² + 3³ + ... + 3¹²⁰. Chứng minh:

a) B chia hết cho 3;

b) B chia hết cho 4;

c) B chia hết cho 13.

Lời giải:

a) B = 3 + 3² + 3³ + ... + 3¹²⁰

= 3(1 + 3 + 3² + ... + 3¹¹⁹)

Vì 3 ⋮ 3 ⇒3(1 + 3 + 3² + ... + 3¹¹⁹) ⋮ 3

Vậy suy ra B ⋮ 3

b) B = 3 + 3² + 3³ + ... + 3¹²⁰

= (3 + 3²) + (3³ + 3⁴) +... + (3¹¹⁹ + 3¹²⁰)

= 3(1 + 3) + 3³(1 + 3) +... + 3¹¹⁹(1 + 3)

= 3.4 + 3³.4 + ... + 3¹¹⁹.4

= 4(3 + 3³ + ... + 3¹¹⁹)

Vì 4 ⋮ 4 ⇒ 4(3 + 3³ + ... + 3¹¹⁹) ⋮ 4

Vậy suy ra B ⋮ 4

c) B = 3 + 3² + 3³ + ... + 3¹²⁰

= (3 + 3² + 3³) + (3⁴ + 3⁵ + 3⁶) +... + (3¹¹⁸ + 3¹¹⁹ + 3¹²⁰)

= 3(1 + 3 + 3²) + 3⁴(1 + 3 + 3²) + ... + 3¹¹⁸(1 + 3 + 3²)

= 3.13 + ... + 3¹¹⁸.13

= 13(3 + 3⁴ + ... + 3¹¹⁸)

Vì 13 ⋮ 13 nên 13(3 + 3⁴ + ... + 3¹¹⁸) ⋮ 13

Vậy suy ra B ⋮ 13

Câu 6: Cho B = 3 + 3² + 3³ + ... + 3¹²⁰. Chứng minh B chia hết cho 13.

Lời giải:

B = 3 + 3² + 3³ + ... + 3¹²⁰

= (3 + 3² + 3³) + (3⁴ + 3⁵ + 3⁶) +... + (3¹¹⁸ + 3¹¹⁹ + 3¹²⁰)

= 3(1 + 3 + 3²) + 3⁴(1 + 3 + 3²) + ... + 3¹¹⁸(1 + 3 + 3²)

= 3.13 + ... + 3¹¹⁸.13

= 13(3 + 3⁴ + ... + 3¹¹⁸)

Vì 13 ⋮ 13 nên 13(3 + 3⁴ + ... + 3¹¹⁸) ⋮ 13

Vậy suy ra B ⋮ 13

Câu 7: Chứng minh rằng biểu thức:

a) x² + 2x + 3 luôn dương với mọi x;

b) −x² + 4x − 5 luôn âm với mọi x.

Lời giải:

a) Ta có: x² + 2x + 3 = (x² + 2x + 1) + 2

= (x + 1)² + 2

Vì (x + 1)² ≥ 0, ∀ x ∈ℝ

Suy ra (x + 1)² + 2 ≥ 2, ∀ x ∈ℝ

Vậy x² + 2x + 3 luôn dương với mọi x

b) Ta có: −x² + 4x − 5 = −(x² − 4x + 4) − 1

= −(x − 2)² − 1

Vì (x − 2)² ≥ 0, ∀ x ∈ℝ

Suy ra −(x − 2)² ≤ 0, ∀ x ∈ℝ

⇒−(x − 2)² − 1 ≤ −1, ∀ x ∈ℝ

Vậy −x² + 4x − 5 luôn âm với mọi x.

Câu 8: Chứng minh 4x − 10 − x² luôn luôn âm với mọi x.

Lời giải:

Ta có: 4x − 10 − x²= −(x² − 4x + 4) − 6

= −(x − 2)² − 6

Vì (x − 2)² ≥ 0, ∀ x ∈ℝ

Suy ra −(x − 2)² ≤ 0, ∀ x ∈ℝ

⇒−(x − 2)² − 6 ≤ −6, ∀ x ∈ℝ

Vậy 4x − 10 − x² luôn luôn âm với mọi x.

Câu 9: Tìm GTNN của B = 2x²+ 3y²+ 4xy − 8x − 2y + 18

Lời giải:

B = 2x² + 3y² + 4xy − 8x − 2y + 18

⇒ 2B = 4x² + 6y² + 8xy − 16x − 4y + 36

= (4x² + 8xy + 4y²) + 2y² − 16x − 4y + 36

= [(2x + 2y)² − 2(2x + 2y).4 + 16] + (2y² + 12y + 18) + 2

= (2x + 2y − 2)² + 2(y² + 6y + 9) + 2

= (2x + 2y − 2)² + 2(y + 3)² + 2 ≥ 2

Dấu “=” xảy ra khi và chỉ khi: $\{\begin{cases} 2 x + 2 y - 2 = 0 \\ y + 3 = 0 \end{cases} \Leftrightarrow \{\begin{cases} x = 4 \\ y = - 3 \end{cases}$

Vậy GTNN của B là 2 khi x = 4; y =−3.

Câu 10: Có bao nhiêu số tự nhiên gồm 5 chữ số phân biệt sao cho 1,2,3 luôn đứng cạnh nhau.

Lời giải:

Gọi số tự nhiên có 5 chữ số $\bar{a b c d e} (a \neq b \neq c \neq d \neq e; a \neq 0)$

Buộc 3 chữ số 1, 2, 3 thành 1 cụm, đặt là A

Hoán vị các chữ số 1, 2, 3 cho nhau ta được 3! = 6 khả năng xảy ra của A

Có 3 cách chọn vị trí cho A trong $\bar{a b c d e}$

Sau khi chọn xong vị trí cho A, 2 chữ số còn lại có $A_{7}^{2} = 42$ cách chọn

Như vậy, sẽ có 3.6.42 = 756 số được tạo thành tính cả trường hợp a = 0.

Xét a = 0:

Khi đó, ta có 2 vị trí cho A, và mỗi vị trí có 6 khả năng xảy ra của A (Hoán vị 1, 2, 3)

Chữ số còn lại có 6 cách chọn

Vậy nếu a = 0 thì sẽ có 72 số được tạo thành.

Vậy, số số tự nhiên có 5 chữ số (a khác 0) thỏa mãn yêu cầu bài toán: 756 − 72 = 684 số tự nhiên.

Câu 11: Có bao nhiêu số tự nhiên có 3 chữ số khác nhau mà tổng các chữ số là chẵn?

Lời giải:

Gọi chữ số cần tìm là $\bar{a b c}$ (a ≠ 0)

Tổng các chữ số là chẵn khi cả 3 số đều chẵn hoặc 1 số chẵn và 2 số lẻ

TH1: cả 3 số đều chẵn.

Ta thấy a có 4 cách chọn, b có 4 cách chọn, c có 3 cách chọn

Suy ra có 4.4.3 = 48 (cách)

TH2: 2 số lẻ và 1 số chẵn.

• Nếu a chẵn thì a có 4 cách chọn, b có 5 cách chọn, c có 4 cách chọn

Suy ra có 4.5.4 = 80 (cách)

• Nếu a lẻ thì a có 5 cách, b và c lần lượt có (4 . 5 + 5 . 4) cách

Suy ra có 5(4 . 5 + 5 . 4) = 200 (cách).

Tổng cộng có: 48 + 80 + 200 = 328 số thỏa mãn.

Câu 12: Không thực hiện phép tính,so sánh các tính sau rồi điền dấu >, < hoặc = và viết vào chỗ chấm cho thích hợp:

a) 357,32× 0,34 ....... 35,732 × 3,4; vì ............

b) 491,5× 0,05 ....... 4,915 × 5; vì...............

Lời giải:

a) 357,32 × 0,34 = 35,732 × 3,4;

Vì 357,32 × 0,34 = 35,732 × 10 × 0,34 = 35,732 × 3,4.

b) 491,5× 0,05 = 4,915 × 5;

Vì 491,5× 0,05 = 4,915 × 100 ×0,05 = 4,915 × 5

Câu 13: Xét vị trí tương đối của hai đường thẳng d₁: x − 2y + 1 = 0 và d₂: −3x + 6y – 10 = 0.

Lời giải:

Ta có: $\frac{1}{- 3} = \frac{- 2}{6} \neq \frac{1}{- 10}$ .

Suy ra hai đường thẳng đã cho song song với nhau.

Câu 14: Cho đoạn thẳng AB. Xác định vị trí của điểm C trên đoạn thẳng AB sao cho CA ≤ CB.

Lời giải:

Xét ba trường hợp:

a) C = M

Ta có: MA = MB nên CA = CB

b) C nằm giữa A và M.

Do C nằm giữa A và M nên CA < MA mà MA = MB nên CA < MB ()

Mặt khác M nằm giữa C và B nên MB < CB (2)

Từ (1) và (2) ta có CA < CB.

c) C nằm giữa M và B

Do C nằm giữa M và B nên CB < MB mà MA = MB nên CB < MA (3)

Mặt khác M nằm giữa A và C nên MA < CA (4)

Từ (3) và (4) ta có: CB < CA.

Vậy nếu điểm C nằm trên đoạn thẳng MA thì ta luôn có CA ≤ CB.

Câu 15: Một thửa ruộng hình chữ nhật có chiều dài 60m, chiều dài bằng $\frac{3}{2}$ chiều rộng, trên thửa ruộng đó người ta trồng lúa cứ 100m² thu hoạch được 50 kg. Hỏi trên cả thửa ruộng thu hoạch được bao nhiêu tạ thóc?

Lời giải:

Chiều rộng của thửa ruộng là:

$60 : \frac{3}{2} = 40 (m)$

Diện tích của thửa ruộng là:

60 × 40 = 2 400 (m²)

Trên cả thửa ruộng thu hoạch được là:

2400 : 100 × 50 = 1 200 (kg) = 12 (tạ)

Đáp số:12 tạ thóc

Câu 16: Giải phương trình: 2^{x + 1} − 2^x = 32.

Lời giải:

Ta có: 2^{x + 1} − 2^x = 32

⇔ 2^x(2 – 1) = 32

⇔ 2^x = 32

⇔ 2^x = 2⁵

⇔ x = 5

Vậy x = 5 là nghiệm của phương trình.

Câu 17: Giải phương trình: 2^{2x + 1} = 32.

Lời giải:

Ta có: 2^{2x + 1} = 32

⇔ 2^{2x + 1} = 2⁵

⇔ 2x + 1 = 5

⇔ x = 2

Vậy x = 2 là nghiệm của phương trình.

Câu 18: Thu gọn biểu thức sau:

A = 1 – 3 + 3² – 3³ + … + 3²⁰²¹ – 3²⁰²²

Lời giải:

Ta có: A = 1 – 3 + 3² – 3³ + … + 3²⁰²¹ – 3²⁰²²

3A = 3 – 3² + 3³ – 3⁴ + … + 3²⁰²² – 3²⁰²³

⇒ 3A + A = (3 – 3² + 3³ – 3⁴ + … + 3²⁰²² – 3²⁰²³) + (1 – 3 + 3² – 3³ + … + 3²⁰²¹ – 3²⁰²²)

⇔ 4A = 1 – 3²⁰²³

$\Leftrightarrow A = \frac{1 - 3^{2023}}{4}$

Vậy $A = \frac{1 - 3^{2023}}{4}$ .

Câu 19: Tính giá trị của biểu thức: P = 1 + 2 + 2² + 2³ + 2⁴ + … + 2²⁰²⁰.

Lời giải:

Ta có: 2P = 2 + 2² + 2³ + 2⁴ + … + 2²⁰²⁰ + 2²⁰²¹

⇒ 2P – P = (2 + 2² + 2³ + 2⁴ + … + 2²⁰²⁰ + 2²⁰²¹) – (1 + 2 + 2² + 2³ + 2⁴ + … + 2²⁰²⁰)

⇔ P = 2²⁰²¹ – 1

Vậy P = 2²⁰²¹ – 1.

Câu 20: Tính tổng của tất cả số tự nhiên x, biết x là số có 2 chữ số và 12 < x < 91.

Lời giải:

Ta có: x ∈ {13; 14; 15 ....; 89; 90}.

Số số hạng là: (90 – 13) + 1 = 78 (số)

Tổng của các số tự nhiên x là:

(90 + 13) . 78 : 2 = 4017

Vậy tổng của các số tự nhiên x là 4017.

Câu 21: Cho ∆ABC có 3 góc nhọn, AH là đường cao. Vẽ HE vuông góc với AB tại E, HF vuông góc AC tại F .

a) Chứng minh: AE.AB = AF.AC.

b) Cho BH = 3cm, AH = 4cm. Tính AE, BE.

Lời giải:

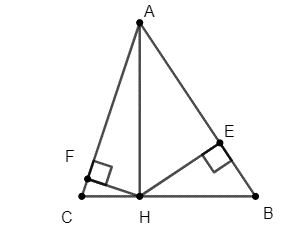
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 61) (ảnh 3)

a) Xét ΔAHB vuông tại H, HE là đường cao nên ta có AH² = AE.AB

Xét ΔAHC vuông tại H, HF là đường cao nên ta có AH² = AF.AC

⇒ AE.AB = AF.AC

b) Xét ΔAHB vuông tại H. Áp dụng định lý Py-ta-go:

AB² = AH² + BH² = 16 + 9 = 25

⇒ AB = 5 (cm)

Có AH² = AE.AB ⇒ AE = 3,2 (cm)

Có BE = AB – AE = 5 – 3,2 = 1,8 (cm)

Câu 22: Chứng minh rằng n⁴ + 2n³ – n² – 2n chia hết cho 24 với mọi số nguyên n.

Lời giải:

Ta có: n⁴ + 2n³ – n² – 2n

= (n⁴ + 2n³) – (n² + 2n)

= n³(n + 2) – n(n + 2)

= (n³ – n)(n + 2)

= n(n² – 1)(n + 2)

= (n – 1)n(n + 1)(n + 2)

Ta thấy (n – 1)n(n + 1)(n + 2) là tích bốn số nguyên liên tiếp nên sẽ chứa một số chia hết cho 2 và một số chia hết cho 4, từ đó suy ra tích bốn số nguyên liên tiếp chia hết cho 8.

Đồng thời, trong bốn số nguyên liên tiếp luôn chứa tích của ba số nguyên liên tiếp, đồng nghĩa với việc tích bốn số nguyên liên tiếp chia hết cho 3.

Mà 24 = 3.8

Vì vậy tích bốn số nguyên liên tiếp chia hết cho 3.8 = 24.

Vậy n⁴ + 2n³ – n² – 2n chia hết cho 24 với mọi số nguyên n.

Câu 23: Có bao nhiêu số nguyên dương không vượt quá 1000 mà chia hết cho 3 hoặc chia hết cho 5?

A. 531 số;

B. 533 số;

C. 332 số;

D. 467 số.

Lời giải:

Đáp án đúng là: D.

• Số chia hết cho 3 có dạng 3a ta có 0 < 3a ≤ 1000 ⇔ 0 < a < 333,3

Mà a nguyên nên có 333 số thỏa mãn.

• Số chia hết cho 5 có dạng 5b ta có 0 < 5b ≤ 1000 ⇔ 0 < b ≤ 200

Nên có 200 số thỏa mãn.

• Số chia hết cho cả 3 và 5 có dạng 15c ta có 0 < 15c ≤ 1000 ⇔ 0 < c < 66,6

Nên có 66 số thỏa mãn.

Do đó số các số thỏa mãn đề bài là: 333 + 200 – 66 = 467.

Câu 24: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, I là trung điểm cạnh SC. Khẳng định nào sau đây là sai?

A. Đường thẳng IO song song với mặt phẳng (SAD);

B. Mặt phẳng (IBD) cắt hình chóp S.ABCD theo thiết diện là một tứ giác;

C. Đường thẳng IO song song với mặt phẳng (SAB);

D. Giao tuyến của hai mặt phẳng (IBD) và (SAC) là IO.

Lời giải:

Đáp án đúng là: B

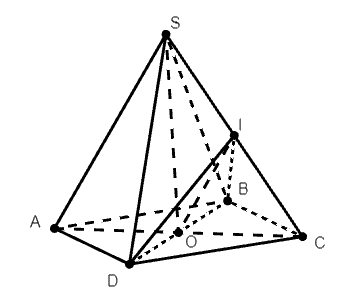
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 61) (ảnh 4)

Ta có: IO//SA ⇒ IO//(SAD) và IO//(SAB) nên đáp án A và đáp án C đúng.

Ta có (SAC) ∩ (IBD) = IO nên đáp án D đúng.

Câu B ta có thiết diện là ∆IBD nên B sai.

Câu 25: Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng với M qua I. Tứ giác AKCM là hình gì?

A. Hình chữ nhật;

B. Hình thoi;

C. Hình vuông;

D. Hình bình hành.

Lời giải:

Đáp án đúng là: A

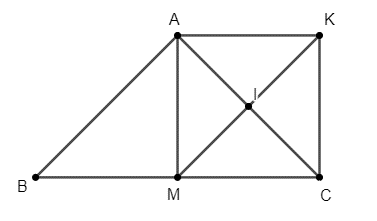
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 61) (ảnh 5)

Xét tứ giác AKCM có:

AC∩MK = {I}

Mà I là chung điểm của hai đoạn AC và MK (gt)

⇒ Tứ giác AKCM là hình bình hành (1)

Vì ∆ABC cân tại A

⇒ AM vừa là đường trung tuyến và cũng là đường cao của ∆ABC.

$\Rightarrow \hat{A M C} = 90 °$ (2)

Từ (1) và (2) suy ra tứ giác AKCM là hình chữ nhật.

Câu 26: Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng với M qua I. Tứ giác AKMB là hình gì?

A. Hình chữ nhật;

B. Hình thoi;

C. Hình vuông;

D. Hình bình hành.

Lời giải:

Đáp án đúng là: D

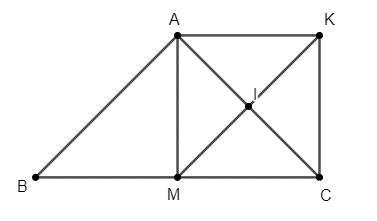
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 61) (ảnh 6)

Tứ giác AKCM có hai đường chéo AC và MK cắt nhau tại trung điểm I của mỗi đường

Suy ra tứ giác AKCM là hình bình hành (1)

Xét ∆ABC cân tại A có AM là đường trung tuyến nên AM cũng là đường cao của ∆ABC hay $\hat{A M C} = 90 °$ (2)

Từ (1) và (2) suy ra tứ giác AKCM là hình chữ nhật.

Vì AKCM là hình chữ nhật nên ta có: AK // CM hay AK // BM và AK = CM.

Mà CM = BM (do M là trung điểm của BC)

Do đó AK = BM và AK // BM.

Từ đó suy ra tứ giác AKMB là hình bình hành.

Câu 27: Khi nhân một số với 205, do vô ý Tâm đã quên viết chữ số 0 của số 205 nên tích giảm đi 42 120 đơn vị. Tìm tích đúng của phép nhân đó.

Lời giải:

Số 205 mà bỏ chữ số 0 thì thành số 25. Như vậy Tâm đã viết nhầm làm giảm 1 thừa số đi số đơn vị là:

205 – 25 = 180 (đơn vị)

Do đó tích giảm đi 180 lần thừa số kia, mà tích giảm đi 42120 đơn vị nên thừa số kia là :

42 120 : 180 = 234

Tích đúng là:

234 ´ 205 = 47 970

Đáp số: 47 970.

Câu 28: Một người nông dân mua một con bò giá 10 triệu, rồi bán đi với giá 15 triệu, sau đó mua lại giá 20 triệu rồi lại bán đi với giá 17 triệu. Người bán bò lãi bao nhiêu tiền?

Lời giải:

Người bán hàng lãi số tiền là:

(15 – 10) – 20 + 17 = 2 (triệu đồng)

Đáp số: 2 triệu đồng.

Câu 29: 88 – 8 + 8 + 8 +…+8 (11 số 8).

Tính bằng cách thuận tiện nhất.

Lời giải:

88 – 8 + 8 + 8 +…+8

= 88 – 8 ´ 11

= 88 – 88 = 0.

Câu 30: Tính số trung bình cộng của các số sau: 3; 5; 9; 10; 13.

Lời giải:

Trung bình cộng của các số trên là:

$\frac{3 + 5 + 9 + 10 + 13}{5} = \frac{40}{5} = 8$

Vậy trung bình cộng của các số 3; 5; 9; 10; 13 là 8.

Câu 31: Tính:

a) (x³ + 3x² – 5x – 1)(4x – 3);

b) $(- 2 x^{2} + 4 x + 6) (- \frac{1}{2} x + 1)$

Lời giải:

a) (x³ + 3x² – 5x – 1)(4x – 3);

= 4x⁴ – 3x³ + 12x³ – 9x² – 20x² + 15x – 4x + 3

= 4x⁴ + (−3x³ + 12x³) + (−9x² – 20x²) + (15x – 4x) + 3

= 4x⁴ + 9x³ – 29x² + 11x + 3.

b) $(- 2 x^{2} + 4 x + 6) (- \frac{1}{2} x + 1)$ .

= x³ – 2x² – 2x² + 4x – 3x + 6

= x³ – 4x² + x + 6.

Câu 32: Cho tam giác ABC vuông tại A, đường cao AH, I là trung điểm của AB, lấy K đối xứng với B qua H. Qua A dựng đường thẳng song song với BC cắt HI tại D.

a) Tứ giác AKHD là hình gì?

b) Chứng minhAHBD là hình chữ nhật.

Lời giải:

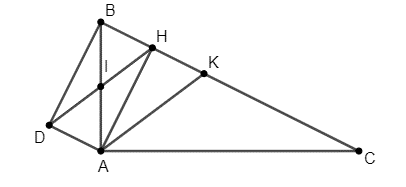
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 61) (ảnh 7)

a) Ta có: H; I lần lượt là trung điểm của BK và AB nên suy ra

HI là đường trung bình của ∆ABK

Suy ra HI // AK hay DH // AK (1)

Mặt khác theo giả thiết ta có: AD // HK (2)

Từ (1) và (2) suy ra tứ giác AKHD là hình bình hành.

b) Vì AKHD là hình bình hành nên:

AD = HK = BH

Mà AD//BH nên AHBD là hình bình hành.

Lại có: $\hat{A H B} = 90 °$

Suy ra AHBD là hình chữ nhật.

Câu 33: Chứng minh rằng A = x⁴ + 2x³ – x² – 2x chia hết cho 24 với mọi số nguyên x.

Lời giải:

Ta có: A = x⁴ + 2x³ – x² – 2x

= (x⁴ – x³) + (3x³ – 3x²) + (2x² – 2x)

= x³(x – 1) + 3x²(x – 1) + 2x(x – 1)

= (x – 1)(x³ + 3x² + 2x)

= (x – 1)x(x² + x + 2x + 2)

= (x – 1)x[x(x + 1) + 2(x + 1)]

= (x – 1)x(x + 1)(x + 2).

Ta thấy x ∈ ℤ thì A là tích của 4 số liên tiếp nên chắc chắc A ⋮ 2; A ⋮ 3; A ⋮ 4.

Từ đó suy ra A ⋮ (2.3.4) hay A ⋮ 24 (đpcm).

Câu 34: Lớp 5A có một số học sinh. Biết số học sinh nữ bằng $\frac{2}{3}$ số học sinh cả lớp. Hỏi số học sinh nam chiếm bao nhiêu phần trăm số học sinh cả lớp?

Lời giải:

Số học sinh nam chiếm số phần trăm số học sinh cả lớp là:

$(1 - \frac{2}{3}) \times 100 % = \frac{1}{3} \times 100 % = 33,33 %$

Đáp số: 33,33%

Câu 35: Phân tích đa thức thành nhân tử: 36 + 2xy – x² – y².

Lời giải:

36 + 2xy – x² – y²

= 36 – (x² – 2xy + y²)

= 6² – (x – y)²

= (6 + x – y)(6 – x + y)

Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).

Lời giải:

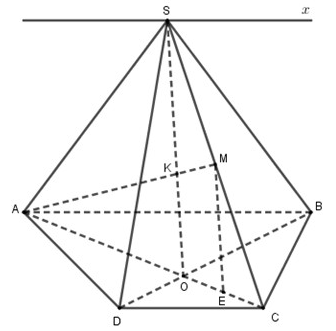
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 61) (ảnh 8)

S là điểm chung của (SAB) và (SCD).

Kẻ Sx // AB // CD

Ta có: AB // CD

AB ⊂ (SAB)

CD ⊂ (SCD)

Suy ra (SAB) ∩ (SCD) = {Sx}

Vậy giao tuyến của hai mặt phẳng (SAB) và (SCD) là Sx.

Câu 37: Cho tam giác ABC vuông ở A, đường cao AH. Kẻ HD vuông góc với AB và HE vuông góc với AC (D trên AB, E trên AC). Gọi O là giao điểm của AH và DE. Chứng minh AH = DE.

Lời giải:

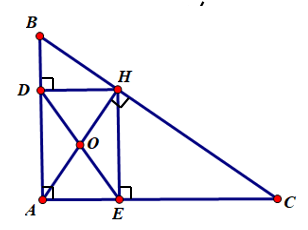
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 61) (ảnh 9)

Xét tứ giác ADHE có 3 góc vuông

$\hat{A} = \hat{D} = \hat{E} = 90 °$

⇒ ADHE là hình chữ nhật

Mà AH, DE là 2 đường chéo

⇒ AH = DE (đpcm)

Vậy AH = DE.

Câu 38: Cho đường tròn (O; R), đường kính AB và tiếp tuyến Ax. Từ điểm C thuộc Ax, kẻ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm). Gọi giao điểm của CO và AD là I. Chứng minh: CO ⊥ AD.

Lời giải:

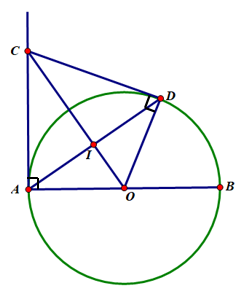
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 61) (ảnh 10)

Ta có CA, CD là hai tiếp tuyến của (O) cắt nhau tại C.

Suy ra CA = CD.

Khi đó C nằm trên đường trung trực của đoạn thẳng AD (1)

Lại có OA = OD = R.

Suy ra O nằm trên đường trung trực của đoạn thẳng AD (2)

Từ (1), (2), suy ra CO là đường trung trực của đoạn thẳng AD.

Vậy CO ⊥ AD tại I.

Câu 39: Số các ước tự nhiên của 252 là bao nhiêu? Liệt kê các ước của 252.

Lời giải:

Ta có:

252 = 2².3².7

Số 252 có số ước là:

(2 + 1).(2 + 1).(1 + 1) = 18 (ước)

Ư(252) = {1; 2; 3; 4; 6; 7; 9; 12; 14; 18; 21; 28; 36; 42; 63; 84; 126; 252}

Vậy số 252 có 18 ước.

Câu 40: Tìm các ước nguyên tố của 36.

Lời giải:

Ta có: 36 = 2².3²

Số 36 có số ước là:

(2 + 1).(2 + 1) = 9 (ước)

Ư(36) = {1; 2; 3; 4; 6; 9; 12; 18; 36}

Vậy Ư(36) = {1; 2; 3; 4; 6; 9; 12; 18; 36}.

Từ khóa :

Giải bài tập

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

227

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

263

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

286

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

236