Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 96) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 96)
Câu 1: Phân tích đa thức sau thành nhân tử: x2 + 6x + 9.
Lời giải:
Ta có:
x2 + 6x + 9
= x2 + 2 . 3 . x + 32
= (x + 3)2.
Câu 2: Tập xác định của hàm số y = logx là:
A. [0; +∞)
B. (0; +∞)
C. (–∞; +∞)
D. [10; +∞).
Lời giải:
Đáp án đúng là: B
Hàm số y = logx xác định
⇔ x > 0
Suy ra tập xác định của hàm số y = logx là (0; +∞)
Vậy ta chọn đáp án B.
Câu 3: Cho x, y là các số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là sai?
A. xm . yn = (xy)m+n
B. (xy)n = xn . yn
C. xm . xn = xm+n
D. (xm)n = xmn.
Lời giải:
Đáp án đúng là: A
Vì không thể nhân hai mũ khác cơ số, khác cả số mũ nên đáp án A sai
Ta chỉ có thể nhân 2 mũ có cùng cơ số
xm . xn = xm+n
Vậy ta chọn đáp án A.
Câu 4: Cho hàm số y = – x3 + 3x2 + 3mx – 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
A. m < 1
B. m ≥ 1
C. m ≤ –1
D. m ≥ –1.
Lời giải:
Đáp án đúng là: C
Ta có y’ = – 3x2 + 6x + 3m ≤ 0, ∀x > 0
⇔ 3m ≤ 3x2 – 6x, ∀x > 0
⇔ 3m ≤ 3(x2 – 2x + 1) – 3, ∀x > 0
⇔ 3m ≤ 3(x – 1)2 – 3, ∀x > 0
Vì 3(x – 1)2 ≥ 0 với mọi x
Nên 3(x – 1)2 – 3 ≥ –3 với mọi x
Suy ra 3x2 – 6x nhỏ nhất bằng –3 khi x = 1
Do đó 3m ≤ –3 ⇔ m ≤ –1
Vậy ta chọn đáp án C.
Câu 5: Cho 4 chữ số 1, 5, 8, 9 có thể viết được mấy số có 4 chữ số khác nhau từ các chữ số trên.
Lời giải:
Có 4 cách chọn chữ số hàng nghìn
Có 3 cách chọn chữ số hàng trăm
Có 2 cách chọn chữ số hàng chục
Có 1 cách chọn chữ số hàng đơn vị
Suy ra lập được số các số có 4 chữ số khác nhau từ các chữ số 1, 5, 8, 9, là:
4 × 3 × 2 × 1 = 24 (số)
Vậy lập được 24 số thỏa mãn yêu cầu đề bài.
Câu 6: Thực hiện phép tính: (102 + 112 + 122) : (132 + 142).
Lời giải:
Ta có:
(102 + 112 + 122) : (132 + 142)
= (100 + 121 + 144) : (169 + 196)
= 365 : 365 = 1.
Câu 7: Phân tích đa thức thành nhân tử: (x – 1)(x – 2)(x + 7)(x + 8) + 8.
Lời giải:
Ta có:
(x – 1)(x – 2)(x + 7)(x + 8) + 8
= (x – 1)(x + 7)(x – 2)(x + 8) + 8
= (x2 + 6x – 7)(x2 + 6x – 16) + 8
Đặt x2 + 6x – 7 = t, ta được
t(t – 9) + 8 = t2 – 9t + 8 = t2 – 8t – t + 8 = t(t – 8) – (t – 8) = (t – 8)(t – 1)
Thay t = x2 + 6x – 7 ta có
(x2 + 6x – 7 – 8)( x2 + 6x – 7 – 1) = (x2 + 6x – 15)( x2 + 6x – 8)
Vậy (x – 1)(x – 2)(x + 7)(x + 8) + 8 = (x2 + 6x – 15)( x2 + 6x – 8).
Câu 8: Khai triển (x – 2)2.
Lời giải:
Ta có:
(x – 2)2 = x2 – 2 . x . 2 + 22 = x2 – 4x + 4
Vậy (x – 2)2 = x2 – 4x + 4.
Câu 9: Phân tích đa thức sau thành nhân tử bằng phương pháp nhóm hạng tử:
x2 – 2x – 4y2 – 4y.
Lời giải:
Ta có:
x2 – 2x – 4y2 – 4y
= (x2 – 4y2) – (2x + 4y)
= (x – 2y)(x + 2y) – 2(x + 2y)
= (x + 2y)(x – 2y – 2)
Vậy x2 – 2x – 4y2 – 4y = (x + 2y)(x – 2y – 2).
Câu 10: Phân tích đa thức thành nhân tử: x3 – 7x – 6.
Lời giải:
Ta có: x3 – 7x – 6
= x3 – x2 + x2 – x – 6x – 6
= x2(x – 1) + x(x – 1) – 6(x + 1)
= (x – 1)(x2 + x) – 6(x + 1)
= (x – 1)x(x + 1) – 6(x + 1)
= (x + 1)(x2 – x – 6)
= (x + 1)(x2 – 3x + 2x – 6)
= (x + 1)[x(x – 3) + 2(x – 6)]
= (x + 1)(x – 3)(x + 2)
Vậy x3 – 7x – 6 = (x + 1)(x – 3)(x + 2).
Câu 11: Cho A = 5n+2 + 26 . 5n + 82n + 1. Chứng minh A ⋮ 59.
Lời giải:
Ta có:
A = 5n+2 + 26 . 5n + 82n + 1
A = 5n . 52 + 26 . 5n + 82n . 8
A = 5n . 25 + 26 . 5n + 82n . 8
A = 5n (25 + 26) + 82n . 8
A = 51 . 5n + 64n . 8
Vì 64 : 59 dư 5 nên 64n : 59 dư 5n
Suy ra 51 . 5n + 64n . 8 chia 59 dư
51 . 5n + 5n . 8 = 5n(51 + 8) = 59 . 5n
Mà 59 . 5n ⋮ 59
Suy ra A ⋮ 59
Vậy A ⋮ 59.
Câu 12: Hình đa diện có các đỉnh là tâm các mặt của một hình bát diện đều là một hình
A. nhị thập diện đều;
B. tứ diện đều;
C. bát diện đều;
D. lập phương.
Lời giải:
Đáp án đúng là: D
Hình đa diện có các đỉnh là tâm các mặt của một hình bát diện đều là một hình lập
Câu 13: Cho ABCD và ACNM là hai hình bình hành chỉ có chung đường chéo AC. Khi đó có thể kết luận gì về bốn điểm B, M, D, N?
A. B, M, D, N tạo thành tứ diện;
B. B, M, D, N tạo thành tứ giác;
C. B, M, D, N thẳng hàng;
D. Chỉ có ba trong số bốn điểm B, M, D, N thẳng hàng.
Lời giải:
Đáp án đúng là: A
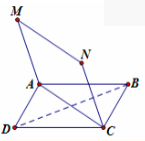
Vì ABCD và ACNM là hai hình bình hành chỉ có chung đường chéo AC nên B, M, D, N không đồng phẳng.
Mà MN // AC còn AC cắt BD nên BD và MN chéo nhau.
Vậy B, M, D, N tạo thành tứ diện.
Câu 14: Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?
A. 0;
B. 2;
C. vô số;
D. 1.
Lời giải:
Đáp án đúng là: D
Vì a và b chéo nhau, mà có duy nhất một mặt phẳng chứa hai đường thẳng cắt nhau nên có duy nhất một mặt phẳng chứa a và song song với b.
Câu 15: Phương trình nào tương đương với sin2x – cos2x – 1 = 0
A. cos 2x = 1;
B. cos 2x = –1;
C. 2cos2x – 1 = 0;
D. (sin x – cos x)2 = 1.
Lời giải:
Đáp án đúng là: B
sin2x – cos2x – 1 = 0 ⇔ cos2x – sin2x = –1 ⇔ cos2x = –1
Câu 16: Tìm số nghiệm của phương trình: 2x + 3x + 4x + … + 2017x + 2018x = 2017 – x
A. 2017;
B. 1;
C. 0;
D. 2016.
Lời giải:
Đáp án đúng là: B
y = 2x + 3x + 4x + … + 2017x + 2018x
y’ = 2xln2 + 3xln3 + 4xln4 + … + 2017xln2017 + 2018xln2018 > 0, ∀x
Do đó hàm số đồng biến trên R
Y = 2017 – x ⇒ y’ = -1 < 0, ∀x ⇒ Hàm số nghịch biến trên R.
⇒ Phương trình 2x + 3x + 4x + … + 2017x + 2018x có tối đa 1 nghiệm
Ta có x = 0 thỏa mãn phương trình.
⇒ x = 0 là nghiệm duy nhất của phương trình đã cho.
Câu 17: Cho f(x) mà đồ thị hàm số y = f’(x) như hình bên. Hàm số y = f(x – 1) + x2 – 2x đồng biến trên khoảng?
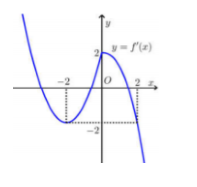
A. (1; 2);
B. (-1; 0);
C. (0; 1);
D. (-2; -1).
Lời giải:
Đáp án đúng là: A
Ta có: y’ = f’(x – 1) + 2x – 2 = 0 ⇔ f’(x – 1) + 2(x – 1) = 0.
Đặt t = x – 1 ta có f’(t) + 2t = 0 ⇔ f’(t) – (-2t) = 0
Vẽ đồ thị hàm số y = f’(t) và y = -2t trên cùng mặt phẳng tọa độ ta có:
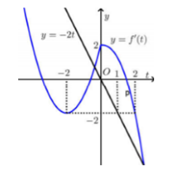
Xét y’ ≥ 0 ⇔ f’(t) ≥ -2t ⇒ Đồ thị hàm số y = f’(t) nằm trên đường thẳng y = -2t.
Xét x ∈ (1; 2) ⇒ t ∈ (0; 1) ⇒ thỏa mãn.
Xét x ∈ (-1; 0) ⇒ t ∈ (-2; -1) ⇒ không thỏa mãn.
Xét x ∈ (0; 1) ⇒ t ∈ (-1; 0) ⇒ không thỏa mãn.
Xét x ∈ (-2; -1) ⇒ t ∈ (-3; -2) ⇒ không thỏa mãn.
Câu 18: Trong hình học không gian:
A. Điểm luôn phải thuộc mặt phẳng;
B. Điểm luôn luôn không thuộc mặt phẳng;
C. Điểm vừa thuộc mặt phẳng đồng thời vừa không thuộc mặt phẳng;
D. Điểm có thể thuộc mặt phẳng, có thể không thuộc mặt phẳng.
Lời giải:
Đáp án đúng là: D
Điểm có thể nằm trên mặt phẳng đã cho hoặc không nằm trên mặt phẳng đó.
Câu 19: Phương trình 4x + 6x = 25x + 2 có tập nghiệm là:
A. {0};
B. {2};
C. {0; 2};
D. {0; 1; 2}.
Lời giải:
Đáp án đúng là: B
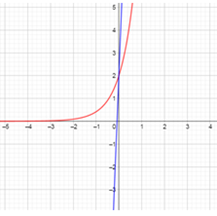
Sử dụng sự tương giao giữa 2 đồ thị hàm số y = 4x + 6x; y = 25x + 2 được nghiệm duy nhất x = 2.
Câu 20: Đồ thị hàm số y = x3 – (3m + 1)x2 + (m2 + 3m + 2)x + 3 có điểm cực tiểu và điểm cực đại nằm về hai phía của trục tung khi:
A. 1 < m < 2;
B. –2 < m < –1;
C. 2 < m < 3;
D. –3 < m < –2.
Lời giải:
Đáp án đúng là: B
y = x3 – (3m + 1)x2 + (m2 + 3m + 2)x + 3
y’ = 3x2 – (6m + 2)x + m2 + 3m + 2
Để cực tiểu và cực đại của đồ thị hàm số y nằm về hai phía của trục tung thì x1.x2 < 0, với x1, x2 là hai nghiệm của phương trình y’ = 0.
⇔ 3(m2 + 3m + 2) < 0 ⇔ m2 + 3m + 2 < 0 ⇔ -2 < m < -1
Câu 21: Gọi S là tập hợp tất cả các số tự nhiên gồm 5 chữ số đôi một khác nhau được lập từ các chữ số 5, 6, 7, 8, 9. Tính tổng tất các số thuộc tập S.
A. 9 333 420;
B. 46 666 200;
C. 9 333 240;
D. 46 666 240.
Lời giải:
Đáp án đúng là: C
Số phần tử của tập S là 5! = 120 số.
Mỗi số 5, 6, 7, 8, 9 có vai trò như nhau và xuất hiện ở hàng đơn vị 4! = 24 lần
Tổng các chữ số xuất hiện ở hàng đơn vị là 4!.(5 + 6 + 7 + 8 + 9) = 840
Tương tự với các chữ số hàng chục, hàng trăm, hàng nghìn và hàng chục nghìn.
Vậy tổng tất cả các số thuộc tập S là 840.(104+103+102+10+1) = 9 333 240
Câu 22: Có bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau trong đó chứa các chữ số 3, 4, 5 và chữ số 4 đứng cạnh chữ số 3 và chữ số 5?
A. 1470;
B. 750;
C. 2940;
D. 1500.
Lời giải:
Đáp án đúng là: D
Sắp xếp cụm số 3,4,5 có 2 cách sắp xếp là 345 và 543
TH1: Cụm 2 số 3,4,5 đứng đầu có: 2.7.6.5 = 240 số thỏa mãn
TH2: Cụm 3 số 3,4,5 không đứng đầu có 3 cách sắp xếp là x345xx; xx345x; xxx345
3 chữ số còn lại có: 6.6.5 = 180 cách chọn và sắp xếp
Do đó có 2.3.180 = 1080 số thỏa mãn
Theo quy tắc cộng có:
420 + 1080 = 1500 số thỏa mãn yêu cầu bài toán.
Câu 23: Cho khối đa diện đều (p; q) chỉ số q là
A. Số mặt của đa diện
B. Số đỉnh của đa diện
C. Số cạnh của đa diện
D. Số các mặt đi qua mỗi đỉnh.
Lời giải:
Đáp án đúng là: A
Khối đa diện đều {p; q} thì chỉ số p là số đỉnh của đa diện; q là số mặt của đa diện.
Vậy đáp án đúng là A.
Câu 24: Cho 8 bạn học sinh A, B, C, D, E, F, G, H. Hỏi có bao nhiêu cách xếp 8 bạn đó ngồi xung quanh một bàn tròn có 8 ghế.
A. 40 320 cách
B. 5 040 cách
C. 720 cách
D. 40 319 cách.
Lời giải:
Đáp án đúng là: B
Ta thấy xếp các vị trí theo một hình tròn nên ta phải cố định vị trí của một bạn
Ta chọn cố định vị trí của A, sau đó xếp vị trí cho 7 bạn còn lại
Bạn thứ nhất có 7 cách xếp
Bạn thứ hai có 6 cách xếp
…
Bạn thứ 7 có 1 cách xếp
Suy ra có 7 . 6 . 5 . 4 . 3 . 2 . 1 = 5 040 cách
Vậy ta chọn đáp án B.
Câu 25: Số đo mỗi góc của ngũ giác đều là:
A. 108°
B. 180°
C. 90°
D. 60°.
Lời giải:
Đáp án đúng là A
Tổng số đo các góc của ngũ giác là: 180°(5 – 2) = 540°
Vì ngũ giác đều có 5 góc bằng nhau nên số đo mỗi góc là:
540° : 5 = 108°
Vậy ta chọn đáp án A.
Câu 26: Trong không gian cho đường thẳng △ không nằm trong mp (P), đường thẳng △ được gọi là vuông góc với mp (P) nếu:
A. vuông góc với hai đường thẳng phân biệt nằm trong mp (P)
B. vuông góc với đường thẳng a mà a song song với mp (P)
C. vuông góc với đường thẳng a nằm trong mp (P)
D. vuông góc với mọi đường thẳng nằm trong mp (P).
Lời giải:
Đáp án đúng là D
Đường thẳng △ được gọi là vuông góc với mặt phẳng (P) nếu △ vuông góc với mọi đường thẳng trong mặt phẳng (P).(ĐN đường thẳng vuông góc với mặt phẳng).
Vậy ta chọn đáp án D.
Câu 27: Đa thức 12x – 36 – x2 bằng:
A. (x + 6)2
B. (–x – 6)2
C. (–x + 6)2
D. – (x – 6)2.
Lời giải:
Đáp án đúng là: D
Ta có:
12x – 36 – x2 = – (x2 – 12x + 36) = – (x – 6)2
Vậy ta chọn đáp án D.
Câu 28: Gọi S là tập hợp các số tự nhiên có hai chữ số. Trong các số: 7; 15; 106; 99, số nào thuộc và số nào không thuộc tập S? Dùng kí hiệu để trả lời.
Lời giải:
Vì S là tập hợp các số tự nhiên có hai chữ số nên tập S là tập hợp các số tự nhiên lớn hơn 9 và nhỏ hơn 100.
Do đó: S = {x| x là số tự nhiên và 9 < x < 100}.
Nhận thấy: 15; 99 là phần tử của S, 7; 106 không là phần tử của S
Vậy: 7 ∉ S; 15 ∈ S; 106 ∉ S; 99 ∈ S.
Câu 29: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – y + 2 = 0. Viết phương trình đường thẳng d’ là ảnh của d qua phép quay tâm O góc quay –90°.
A. d’: x + 3y + 2 = 0.
B. d’: x + 3y – 2 = 0.
C. d’: 3x – y – 6 = 0.
D. d’: x – 3y – 2 = 0.
Lời giải:
Đáp án đúng là: B
Qua phép quay tâm O góc quay –90° đường thẳng d biến thành đường thẳng d′ vuông góc với d
Phương trình đường thẳng d′ có dạng: x + 3y + m = 0
Lấy A(0; 2) ∈ d. Qua phép quay tâm O góc quay –90°, điểm A(0; 2) biến thành điểm B(2; 0) ∈ d′
Khi đó m = –2
Suy ra phương trình đường d′ là x + 3y – 2 = 0
Vậy đáp án cần chọn là B.
Câu 30: Có bao nhiêu phép tịnh tiến biến một đường thẳng thành chính nó?
A. Không có
B. 1
C. 2
D. Vô số.
Lời giải:
Đáp án đúng là: D
Có vô số phép tịnh tiến biến một đường thẳng d thành chính nó. Khi đó, vecto tịnh tiến có giá song song hoặc trùng với đường thẳng d.
Vậy ta chọn đáp án D.
Câu 31: Miền nghiệm của bất phương trình: 3x + 2(y + 3) > 4(x + 1) – y + 3 là nửa mặt phẳng chứa điểm:
A. (3; 0).
B. (3; 1).
C. (3; 2)
D. (0; 0).
Lời giải:
Đáp án đúng là: C
Ta có:
3x + 2(y + 3) > 4(x + 1) – y + 3
⇔ –x + 3y – 1 > 0
Vì –3 + 3.2 – 1 > 0 là mệnh đề đúng nên miền nghiệm của bất phương trình trên chứa điểm có tọa độ (3; 2)
Vậy ta chọn đáp án C.
Câu 32: Trong các mệnh đề mệnh đề nào sai?
A. Phép dời là phép đồng dạng tỉ số k = 1.
B. Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
C. Phép vị tự tỉ số k là phép đồng dạng tỉ số |k|.
D. Phép đồng dạng bảo toàn tỉ số góc.
Lời giải:
Đáp án đúng là: B
Vì phép quay là phép đồng dạng mà phép quay với góc quay α ≠ kπ (k ∈ ℤ) thì không biến đường thẳng thành đường thẳng song song hoặc trùng với nó
Vậy ta chọn đáp án B.
Câu 33: Trong một hộp bút có 2 bút đỏ, 3 bút đen và 2 bút chì. Hỏi có bao nhiêu cách để lấy một cái bút?
A. 12.
B. 6.
C. 2.
D.7
Lời giải:
Đáp án đúng là: D
Chọn 1 bút đỏ có 2 cách
Chọn 1 bút đen có 3 cách
Chọn 1 bút chì có 2 cách
Suy ra có tất cả 2 + 3 + 2 = 7 cách lấy 1 cái bút (quy tắc cộng)
Vậy ta chọn đáp án D.
Câu 34: Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Hai đường thẳng cắt nhau.
B. Ba điểm phân biệt
C. Bốn điểm phân biệt
D. Một điểm và một đường thẳng.
Lời giải:
Đáp án đúng là: A
B sai. Trong trường hợp 3 điểm phân biệt thẳng hàng thì sẽ có vô số mặt phẳng chứa 3 điểm thẳng hàng đã cho.
D sai. Trong trường hợp điểm thuộc đường thẳng đã cho, khi đó ta chỉ có 1 đường thẳng, có vô số mặt phẳng đi qua đường thẳng đó.
C sai. Trong trường hợp 4 điểm phân biệt thẳng hàng thì có vô số mặt phẳng đi qua 4 điểm đó hoặc trong trường hợp 4 điểm mặt phẳng không đồng phẳng thì sẽ tạo không tạo được mặt phẳng nào đi qua cả 4 điểm.
Vậy ta chọn đáp án A.
Câu 35: Với những giá trị nào của m thì đồ thị các hàm số y = 2x + (3 + m) và y = 3x + (5 – m) cắt nhau tại một điểm trên trục tung?
Lời giải:
Đồ thị hai hàm số y = 2x + (3 + m) và y = 3x + (5 – m) cắt nhau tại một điểm trên trục tung nên ta thay hoành độ x = 0 vào:
Hàm số y = 2x + (3 + m) ta được tung độ: y = 3 + m
Hàm số y = 3x + (5 – m) ta được tung độ: y = 5 – m
Vì cùng là tung độ của giao điểm nên 3 + m = 5 – m ⇔ m = 1
Vậy khi m = 1 thì hai đường thẳng đã cho cắt nhau tại một điểm trên trục tung.
Câu 36: Trong không gian cho đường thẳng △ không nằm trong mp (P), đường thẳng ∆ được gọi là vuông góc với mp (P) nếu:
A. vuông góc với hai đường thẳng phân biệt nằm trong mp (P).
B. vuông góc với đường thẳng a mà a song song với mp (P).
C. vuông góc với đường thẳng a nằm trong mp (P).
D. vuông góc với mọi đường thẳng nằm trong mp (P).
Lời giải:
Đáp án đúng là: D
Đường thẳng ∆ được gọi là vuông góc với mặt phẳng (P) nếu ∆ vuông góc với mọi đường thẳng trong mặt phẳng (P). (Định nghĩa đường thẳng vuông góc với mặt phẳng).
Vậy ta chọn đáp án D.
Câu 37: Cho đường thẳng d song song với mặt phẳng (α), nếu mặt phẳng (β) chứa d mà cắt (α) theo giao tuyến d’ thì:
A. d ≡ d’
B. d // d’
C. d // (β)
D. d’ // (α).
Lời giải:
Đáp án đúng là: B
Cho đường thẳng d song song với mặt phẳng (α), nếu mặt phẳng (β) chứa d mà cắt (α) theo giao tuyến d’ thì d // d’
Vậy đáp án cần chọn là: B.
Câu 38: Tìm một số thập phân biết rằng khi chia số đó cho 3,25 rồi cộng với 24,56 thì được kết quả một số tự nhiên lớn nhất có hai chữ số.
A. 401,57
B. 238,68
C. 2747,25
D. 241,93.
Lời giải:
Đáp án đúng là: D
Số tự nhiên lớn nhất có hai chữ số là 99.
Giả sử x là số thập phân cần tìm
Theo đề bài ta có x : 3,25 + 24,56 = 99
⇔ x : 3,25 = 99 – 24,56
⇔ x : 3,25 = 74,44
⇔ x = 74,44 × 3,25
⇔ x = 241,93
Suy ra số thập phân cần tìm là 241,93
Vậy ta chọn đáp án D.
Câu 39: Hai xạ thủ cùng bắn vào một tấm bia. Xác suất người thứ nhất bắn trúng là 80%. Xác suất người thứ hai bắn trúng là 70 %. Xác suất hai người cùng bắn trúng là:
A. 50%
B. 32,6%
C. 60%
D. 56%.
Lời giải:
Đáp án đúng là: D
Gọi A là biến cố “người thứ nhất bắn trúng”
Gọi B là biến cố “ người thứ hai bắn trúng”
Suy ra P(A) = 0,8 và P(B) = 0,7
Và AB là biến cố “cả hai người cùng bắn trúng”
Ta có P(AB) = P(A) . P(B) = 0,8 . 0,7 = 0,56 = 56%
Vậy đáp án cần chọn là: D.
Câu 40: Trong mặt phẳng α cho tứ giác ABCD, điểm E ∉ (α). Hỏi có bao nhiêu mặt phẳng phân biệt tạo bởi ba trong năm điểm A, B, C, D, E?
A. 10
B. 7
C. 8
D. 9.
Lời giải:
Đáp án đúng là: B
Điểm E và 2 điểm bất kì trong 4 điểm A, B, C, D tạo thành 6 mặt phẳng, bốn điểm A, B, C, D tạo thành 1 mặt phẳng.
Suy ra có tất cả 7 mặt phẳng.
Vậy đáp án cần chọn là: B.
Câu 41: Chọn câu sai. Tứ giác nào có hai đường chéo bằng nhau.
A. Hình vuông
B. Hình thang cân
C. Hình chữ nhật
D. Hình thoi.
Lời giải:
Đáp án đúng là: D
Trong các hình: hình vuông, hình chữ nhật, hình thang cân, hình thoi thì hình thoi là hình có hai đường chéo không bằng nhau.
Vậy đáp án cần chọn là: D.
Câu 42: Cho tứ giác lồi ABCD và điểm S không thuộc mp(ABCD). Có bao nhiêu mặt phẳng phân biệt xác định bởi 3 trong số các điểm A, B, C, D, S?
A. 5
B. 6
C. 7
D. 4.
Lời giải:
Đáp án đúng là: C
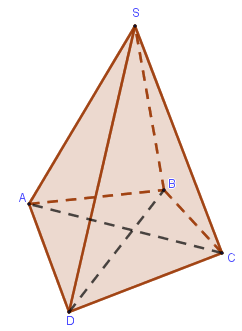
Từ hình vẽ ta thấy có 7 mặt phẳng được xác định bởi các điểm A, B, C, D, S.
Vậy đáp án cần chọn là: C.
Câu 43: Cho 2 đường thẳng a, b cắt nhau và không đi qua điểm A. Xác định được nhiều nhất bao nhiêu mặt phẳng bởi a, b và A?
A. 1
B. 2
C. 3
D. 4.
Lời giải:
Đáp án đúng là: C
Có 3 mặt phẳng gồm (a; b),(A; a),(A; b)
Vậy đáp án cần chọn là: C.
Câu 44: Số mặt phẳng đối xứng của hình bát diện đều là:
A. 5
B. 3
C. 7
D. 9.
Lời giải:
Đáp án đúng là: D
Hình bát diện đều có 9 mặt phẳng đối xứng
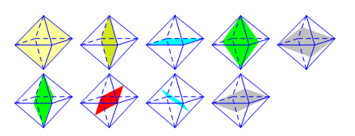
Vậy đáp án cần chọn là: D.
Câu 45: Một số gấp lên 9 lần rồi bớt đi 13 thì được năm chục. Giá trị của số đó là:
A. 63
B. 5
C. 6
D. 7.
Lời giải:
Đáp án đúng là: D
Số cần tìm là: (50 + 13) : 9 = 7
Suy ra số cần tìm là 7
Vậy ta chọn đáp án D.
Câu 46: Quan sát đồ thị hàm số y = f(x) = x2 rồi so sánh f(x1) và f(x2) (với x1 < x2) trong từng trường hợp sau:
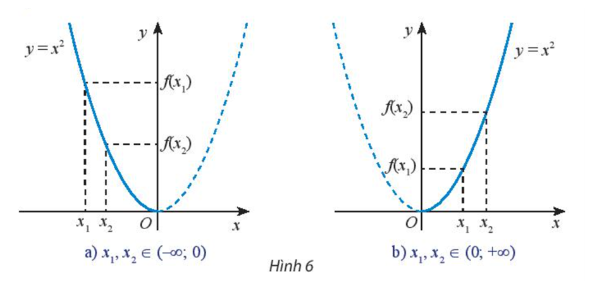
Lời giải:
+) Hình 6a):
Quan sát hình vẽ ta thấy trên trục Oy, f(x1) nằm trên f(x2) nên f(x1) > f(x2)
Vậy với x1, x2 ∈ (–∞; 0) và x1 < x2 thì f(x1) > f(x2).
+) Hình 6b):
Quan sát hình vẽ ta thấy trên trục Oy, f(x1) nằm dưới f(x2) nên f(x1) < f(x2)
Vậy với x1, x2 ∈ (–∞; 0) và x1 < x2 thì f(x1) < f(x2).
Câu 47: Có hai dãy ghế mỗi dãy xếp 5 nam, 5 nữ vào 2 dãy ghế trên. Có bao nhiêu cách nếu:
a) Nam và nữ được xếp tùy ý.
b) Nam 1 dãy ghế nữ 1 dãy ghế.
Lời giải:
a) Vì nam nữ được sắp xếp tùy ý nên sử dụng hoán vị cho 5 nam + 5 nữ = 10 người
Suy ra có 10! = 3 628 800 cách xếp.
b) Chọn 1 dãy xếp nam ngồi có 2 cách.
Xếp 5 bạn nam vào các vị trí trong dãy đã chọn có 5! cách
Xếp nữ vào dãy còn lại có 1 cách
Xếp nữ vào các vị trí trong dãy đó có 5! cách
Suy ra có: 2 . 5! . 1 .5! = 28 800 cách.
Câu 48: “ Nếu ta chia cả tử và mẫu của một phân số cho cùng một … của chúng thì ta được một phân số mới … phân số đã cho”. Các cụm từ thích hợp vào chỗ trống lần lượt là:
A. ước chung, bằng
B. bội chung, lớn nhất
C. số, bằng
D. tích, bằng.
Lời giải:
Đáp án đúng là: A
Dựa vào tính chất cơ bản của phân số:
Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho.
Vậy đáp án cần chọn là: A.
Câu 49: Không gian mẫu khi gieo hai đồng xu là:
A. Ω ={SS; NN; NS; SN}
B. Ω ={SS; NN; SN}
C. Ω ={SS; NN}
D. Ω ={SS; SN}.
Lời giải:
Đáp án đúng là: A
Khi gieo một đồng xu thì có thể ra mặt sấp (S) hoặc mặt ngửa (N).
Do đó không gian mẫu khi gieo hai đồng xu là: Ω ={SS, NN, NS, SN}
Vậy đáp án cần chọn là: A.
Câu 50: Cho tập hợp A={1; 2; 3; 4; a; b}. Xét các mệnh đề sau đây:
(I): “3 ∈ A”.
(II): “{3; 4} ∈ A”.
(III): “{a; 3; b} ∈ A”.
Trong các mệnh đề sau, mệnh đề nào đúng?
A. I đúng
B. I, II đúng
C. II đúng
D. III đúng.
Lời giải:
Đáp án đúng là: A
Vì 3 là một phần tử của tập hợp A nên 3 ∈ A
Vì {3; 4} là một tập con của tập hợp A nên {3; 4} ⊂ A
Vì {3; 4} là một tập con của tập hợp A nên {3; 4} ⊂ A
Vậy ta chọn đáp án A.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.