Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 62)

Ngọc Nguyễn Ngày: 07-08-2023 Tổng hợp kiến thức

312

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 62) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 62)

Câu 1: Một sân chơi hình chữ nhật có chiều rộng là 28 m và chiều dài gấp 4 lần chiều rộng. người ta dùng loại gạch hình vuông có cạnh 50 cm để lát kín sân chơi đó . Hỏi cần ít nhất bao nhiêu xe gạch đủ sân chơi trên? Biết 1 chuyến chở 350 viên gạch và diện tích các mạch vữa không đáng kể.

Lời giải:

Chiều dài của sân chơi đó là:

28 ×4 = 112 (m)

Diện tích sân chơi đó là:

112 × 28 = 3136 (m²) = 31 360 000 (cm²)

Diện tích 1 viên gạch là:

50 × 50 = 2500 (cm²)

Cần số viên gạch để lát kín sân chơi đó là:

31 360 000 : 2500 = 12544 (viên)

Ta có: 12544 : 350 = 35 (dư 294)

Vì 294 viên gạch vẫn cần 1 chuyến nữa để chuyển nên cần số chuyến là:

35 + 1 = 36 (chuyến)

Đáp số: 36 chuyến

Câu 2: Một mảnh đất trong công viên hình chữ nhật có chiều dài 16m và chiều rộng bằng nửa chiều dài. Người ta dự định làm một giàn hoa bên trong mảnh đất đó có hình thoi như hình bên, còn lại sẽ trồng hoa hồng nếu mỗi mét vuông trồng được 4 cây hoa hồng. Hỏi cần bao nhiêu cây hoa hồng để trồng hết phần đất còn lại?

Lời giải:

Chiều rộng là:

16 : 2 = 8 (m)

Diện tích mảnh đất là:

16 ´ 8=128 (m²)

Số hoa hồng cần trồng là:

128 : 4 = 32 (cây)

Đáp số: 32 cây

Câu 3: Cho tam giác ABC, kẻ AH ⊥ BC. Trên tia đối của tia HA, lấy điểm K sao cho HK = HA. Nối KB, KC. Tìm các cặp tam giác bằng nhau trong hình vẽ.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 62) (ảnh 1)

Lời giải:

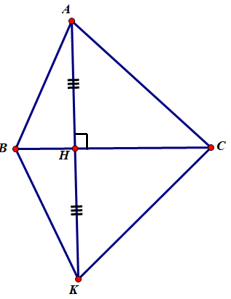
Các cặp tam giác bằng nhau trong hình vẽ là:

ΔABH = ΔKBH (c.g.c)

ΔACH = ΔKCH (c.g.c)

ΔABC = ΔKBC (c.c.c)

Câu 4: Tìm các hệ số a, b, c sao cho đa thức 3x⁴+ ax²+ bx + c chia hết cho đa thức (x – 2) và chia cho đa thức (x²– 1) được thương và còn dư (−7x – 1).

Lời giải:

3x⁴ + ax² + bx + c chia hết x – 2

⇒ 3x⁴ + ax² + bx + c = (x – 2).q(x)

3x⁴ + ax² + bx + c chia x² – 1 được thương v(x) dư –7x – 1

⇒ 3x⁴ + ax² + bx + c = (x² – 1).v(x) –7x – 1

Cho x = 2

⇒ 48 + 4a + 2b + c = 0 (1)

⇒ a + b + c = −11 (2)

Cho x = −1

⇒ 3 + a – b + c = 6

⇒ a – b + c = 3 (3)

Lấy (2) + (3) ⇒ a + c = −4 (4)

⇒ −4 – b = 3

⇒ b = −7

Từ (1) ⇒ 4a + c = −34 (5)

(4) – (5) ⇒ −3a = 30 ⇒ a = −10

⇒ c = 6

Vậy (a; b; c) = (−10; −7; 6)

Câu 5: Tìm a, b, c để đa thức f(x) = x³ + ax² + bx + c chia hết cho x − 2 và chia cho x² − 1 thì dư 2x.

Lời giải:

Gọi q(x); g(x) lần lượt là thương của phép chia f(x) cho x – 2; f(x) cho x² – 1

⇒ f(x) = q(x)(x– 2)

Và f(x) = g(x)(x² – 1) + 2x

⇒ f(2) = 8 + 4a + 2b + c = 0

f(1) = 1 + a + b + c = 2

f(–1) = – 1 + a – b + c = –2

Từ các hệ thức trên ta tìm được:

$a = \frac{10}{3}$ ; b = 1; $c = \frac{10}{3}$

Câu 6: Tìm số có 2 chữ số biết rằng nếu viết thêm chữ số 0 vào vào giữa 2 chữ số của số đó thì ta được số mới gấp 7 lần số phải tìm.

Lời giải:

Gọi số cần tìm là $\bar{a b}$ (0 < a < 10; 0 ≤ b < 10)

Theo đề ra ta có:

$\bar{a 0 b} : \bar{a b} = 7$

Ta có: 100a + b = 7(10a + b)

100a + b = 70a + 7b

100a − 70a = 7b − b

30a = 6b

5a = b

a = 1 (vì nếu b lớn hơn hoặc bằng 2 thì a lớn hơn hoặc bằng 10)

Suy ra b = 5

Vậy số cần tìm là 15.

Câu 7: Tìm số có hai chữ số biết rằng nếu viết chữ số 3 vào giữa hai chữ số đó ta được một số có 3 chữ số gấp 11 lần số cần tìm?

Lời giải:

Gọi số cần tìm là $\bar{a b}$ (0 < a < 10; 0 ≤ b < 10)

Theo đề ra ta có:

$\bar{a 3 b} : \bar{a b} = 11$

Ta có: 100a + b = 11(10a + b)

100a + 30 + b = 110a + 11b

110a − 100a = 30 − 10b

10a = 30 − 10b

Ta có bảng:

(TM)

–1

(TM)

Vậy các số cần tìm là 12; 21; 30.

Câu 8: Cho x + y + z = 1. Chứng minh: $x^{2} + y^{2} + z^{2} \geq \frac{1}{3}$ .

Lời giải:

$x^{2} + y^{2} + z^{2} \geq \frac{1}{3}$

⇔ 3(x²+ y² + z²) ≥ 1

⇔ 3(x²+ y² + z²) ≥ (x+y+z)2

⇔ 3x²+ 3y²+ 3z²− x²− y²− z²− 2xy − 2yz − 2zx ≥ 0

⇔ 2x² + 2y² + 2z² − 2xy − 2yz − 2zx ≥ 0

⇔ (x²− 2xy + y²) + (y²− 2yz + z²) + (z²− 2zx + x²) ≥ 0

⇔ (x − y)² + (y − z)² + (z − x)² ≥ 0 (luôn đúng)

Vậy $x^{2} + y^{2} + z^{2} \geq \frac{1}{3}$ .

Câu 9: Cho p, q là số nguyên tố và phương trình x² − px + q = 0 có nghiệm nguyên dương. Tìm p, q.

Lời giải:

Để phương trình đã cho có nghiệm nguyên dương thì Δ = p² − 4q là số chính phương.

Đặt p²− 4q = k² ⇔ 4q = (p − k)(p + k) với k là số tự nhiên.

Do p − k, p + k cùng tính chẵn, lẻ mà tích của chúng chẵn nên hai số này cùng chẵn.

Mặt khác p − k < p + k và q là số nguyên tố nên:

p − k = 2 và p + k = 2q hoặc p − k = 4 và p + k = q

Nếu p − k = 4 và p + k = q thì q chẵn do đó q = 2 (vô lí vì p + k > p − k).

Nếu p − k = 2 và p + k = 2q thì 2p = 2q + 2 tức p = q + 1. Do đó q chẵn tức q = 2. Suy ra p = 3.

Thử lại ta thấy phương trình: x² − 3x + 2= 0 có nghiệm nguyên dương x = 1 và x = 2.

Vậy p = 3; q = 2.

Câu 10: Tìm các số nguyên tố p và q sao cho 7p + q và pq + 11 cũng là các số nguyên tố.

Lời giải:

Vì p, q là số nguyên tố mà pq+11 cũng là số nguyên tố

⇒ pq chẵn

Giả sử p = 2

⇒ 7p + q = 14 + q

Mà 7p + q là số nguyên tố nên q lẻ

⇒ q = 3; 3k + 1; 3k + 2

Nếu q = 3 thì 14 + 3 =17 là số nguyên tố

2.3 + 11 = 17 là số nguyên tố

⇒ Thỏa mãn

Nếu q = 3k + 1 thì 14 + 3k + 1 = 15 + 3k = 3(5 + k) chia hết cho 3.

⇒ Không thỏa mãn

Nếu q = 3k + 2 thì 2(3k + 2) + 11 = 2.3k + 15 = 3(2k+5) chia hết cho 3.

⇒ Không thỏa mãn

⇒ p = 2; q = 3

Giả sử q = 2

⇒ p lẻ vì 7p+2 là số nguyên tố lớn hơn 3

⇒ p = 3; 3k + 1; 3k + 2

Nếu p = 3 thì 7.3 + 2 = 23 là số nguyên tố

2.3 +11 = 17 là số nguyên tố

⇒ Thỏa mãn

Nếu p = 3k + 1 thì 7(3 + 1) + 2 = 7.3k + 9 = 3(7k + 3) chia hết cho 3

⇒ Không thỏa mãn

Nếu p = 3k + 2 thì 2(3k + 2) + 11 = 2.3k + 15 = 3(2k + 5) chia hết cho 3

⇒ Không thỏa mãn

Do đó p = 3; q = 2

Vậy p = 3; q = 2.

Câu 11: Cho x + y = 2. Tìm giá trị nhỏ nhất của biểu thức: S = x² + y².

Lời giải:

Áp dụng bất đẳng thức Bunhiacopxki, ta có:

(x + y)² ≤ (x² + y²).(1² + 1²)

⇔ 4 ≤ 2.S

⇔ 2 ≤ S

Dấu "=" xảy ra ⇔ x = y = 1

Vậy GTNN của S là 2 tại x = y = 1.

Câu 12: Từ các chữ số 0, 1, 2, 3, 5 có thể lập được bao nhiêu số tự nhiên không chia hết cho 5, gồm 4 chữ số khác nhau?

Lời giải:

Gọi số cần tìm có là $\bar{a b c d}$

• d có 3 cách chọn (d ≠ {0; 5})

• a có 3 cách chọn (a ≠ {0; d})

• b có 3 cách chọn (b ≠ {a; d})

• c có 2 cách chọn

Theo quy tắc nhân có 3 × 3 × 3 × 2 = 54

Vậy có 54 số thỏa mãn yêu cầu.

Câu 13: Từ các chữ số 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên chia hết cho 6, gồm ba chữ số đôi một khác nhau?

Lời giải:

Gọi số cần tìm có là $\bar{a b c}$

Ta có: c ⋮ 2; (a + b + c) ⋮ 3

Các bộ số (a; b; c) thảo mãn là:

{(1; 2; 3); (1; 2; 6); (2; 3; 4); (3; 4; 5)}

Các bộ (1; 2; 3); (3; 4; 5) có 2! = 2 số

Nên 2 bộ này có tổng cộng 4 số.

Các bộ (1; 2; 6); (2; 3; 4) có 2 . 2 . 1 = 4 (số).

Nên 2 bộ này có tổng cộng 8 số.

Vậy có tất cả 12 số thỏa mãn.

Câu 14: Tìm tập hợp bội của 6.

Lời giải:

Tập hợp bội của 6 là:

B(6) ={0; 12; 24; 30; 36; ...}

Vậy B(6) ={0; 12; 24; 30; 36; ...}.

Câu 15: Xác định parabol (P): y = ax² + bx + 2, biết rằng (P) đi qua hai điểm

M (1; 5) và N (−2; 8).

Lời giải:

Vì (P) đi qua điểm M (1; 5) và N (−2; 8) nên ta có hệ phương trình:

$\{\begin{matrix} a + b + 2 = 5 \\ 4 a - 2 b + 2 = 8 \end{matrix} \Leftrightarrow \{\begin{matrix} a = 2 \\ b = 1 \end{matrix}$

Vậy (P): y = 2x² + x + 2.

Câu 16: Cho parabol (P): y = ax² + bx + c có trục đối xứng là đường thẳng x = 1.

Tính 4a + 2b.

Lời giải:

Do parabol (P): y = ax² + bx + c có trục đối xứng là đường thẳng x = 1 nên $\frac{- b}{2 a} = 1$

⇔ 2a = – b ⇔ 2a + b = 0 ⇔ 2(2a + b) = 0 ⇔ 4a + 2b = 0

Vậy 4a + 2b = 0.

Câu 17: Cho biết 3 người làm cỏ một cánh đồng hết 6 giờ. Hỏi 12 người (có cùng năng suất) làm cỏ cánh đồng đó hết bao nhiêu thời gian?

Lời giải:

Gọi thời gian để 12 người làm cỏ cánh đồng đó là x (giờ) (x > 0)

Trên cùng 1 cánh đồng thì thời gian làm cỏ và số người là 2 đại lượng tỉ lệ nghịch

$\Leftrightarrow \frac{3}{12} = \frac{x}{6}$

⇒ x = 1,5

Câu 18: Tìm số nguyên n để n³ – 3 chia hết cho n − 2.

Lời giải:

Ta có: n³ – 3 = n³ – 8 + 5

= (n − 2)(n²+ 2n + 4) + 5

Do đó: n³ – 3 chia hết cho n – 2

⇔ 5 chia hết cho n – 2

Suy ra n – 2 ∈ {±1; ±5}

Ta có bảng:

n – 2

−1

−5

(TM)

−3

(TM)

Vậy n ∈ {−3; 1; 3; 7}.

Câu 19: Phân tích đa thức thành nhân tử: x³ – x²y – xy² + y³.

Lời giải:

Ta có: x³ – x²y – xy² + y³

= x²(x – y) – y²(x – y)

= (x² – y²)(x – y)

= (x – y)²(x + y)

Câu 20: Phân tích đa thức thành nhân tử: –6x² – 9xy + 15y².

Lời giải:

–6x² – 9xy + 15y²

= –(6x² + 9xy – 15y²)

= –(6x² – 6xy + 15xy – 15y²)

= –[6x(x – y) + 15y(x – y)]

= –[(x – y)(6x + 15y)]

Câu 21: Tính nhanh: 95,72 x 3,57 + 3,57 x 4,28

Lời giải:

95,72 x 3,57 + 3,57 x 4,28

= 3,57 x (95,72 + 4,28)

= 3,57 x 100 = 357

Câu 22: Tính nhanh: 17,8 x 99 + 17 + 0,8.

Lời giải:

17,8 x 99 + 17 + 0,8

= 17,8 x 99 + 17,8

= 17,8 x (99 + 1)

= 17,8 x 100 = 1 780.

Câu 23: Trong các số sau số nào là số nguyên tố: 20; 31; 45?

Lời giải:

Ta có

• 20 = 2².5 nên 20 không phải là số nguyên tố

• 31 = 1.31 nên 31 là số nguyên tố

• 45 = 3².5 nên 45 không phải là số nguyên tố

Vậy 31 là số nguyên tố.

Câu 24: Chứng minh 6 không phải là số nguyên tố.

Lời giải:

Ta có: 6 = 2.3

Do đó 6 chia hết cho 2 và 3

Vậy 6 không phải là số nguyên tố.

Câu 25: Diện tích hình chữ nhật thay đổi như thế nào nếu: Chiều dài tăng 2 lần, chiều rộng không đổi?

Lời giải:

Giả sử hình chữ nhật ban đầu có chiều dài là a, chiều rộng là b

Diện tích: S = a.b

Chiều dài tăng 2 lần, chiều rộng không đổi

⇒ a’ = 2a, b’ = b

⇒ S’ = a’.b’ = 2a.b = 2ab = 2.S

Vậy diện tích tăng 2 lần.

Câu 26: Diện tích hình chữ nhật thay đổi như thế nào nếu: Chiều dài và chiều rộng tăng 3 lần?

Lời giải:

Giả sử hình chữ nhật ban đầu có chiều dài là a, chiều rộng là b

Diện tích: S = a.b

Chiều dài và chiều rộng tăng 3 lần

⇒ a’ = 3a; b’ = 3b

⇒ S’ = a’.b’ = 3a.3b = 9ab = 9S

Vậy diện tích tăng 9 lần.

Câu 27: Cho hàm số: y = x^-4. Tìm khẳng định sai.

A. Đồ thị hàm số có một trục đối xứng

B. Đồ thị hàm số đi qua điểm (1; 1)

C. Đồ thị hàm số có hai đường tiệm cận

D. Đồ thị hàm số có một tâm đối xứng

Lời giải:

Đáp án đúng là: D

Ta có: $y = x^{- 4} = \frac{1}{x^{4}}$

Do đó đồ thị hàm số nhận trục tung làm trục đối xứng.

Thay A(1; 1) vào đồ thị ta có:

$1 = \frac{1}{1^{4}}$ (luôn đúng)

Đồ thị hàm số có tiệm cận đứng x = 0 và tiệm cận ngang y = 0.

Vậy đáp án D có khẳng định sai.

Câu 28: Tìm giá trị nhỏ nhất của biểu thức: A = |x – 3| + |x – 5| + |x – 7|.

Lời giải:

Ta có: A = |x – 3| + |x – 5| + |x – 7|

= |x – 3| + |x – 5| + |7 – x| ≥ | x − 3 + 7 − x | + | x − 5 |

= | 4 | + | x − 5 |

= 4 + | x − 5 |.

Do |x – 5| ≥ 0 nên 4 + |x – 5| ≥ 4

⇒ |x – 3| + |x – 5| + |7 – x| ≥ 4

Dấu "=" xảy ra khi |x – 5| = 0

⇔ x − 5 = 0

⇔ x = 5.

Vậy GTNN của A = 4 khi x = 5.

Câu 29: Dựa vào tính chất liên hệ giữa thứ tự và phép cộng. Chứng minh rằng: a > b khi và chỉ khi a – b > 0.

Lời giải:

Ta có: a > b ⇔ a – b > b – b = 0

Vậy a > b khi và chỉ khi a – b > 0.

Câu 30: Dựa vào tính chất liên hệ giữa thứ tự và phép cộng. Chứng minh rằng: a + b > c khi và chỉ khi a > c – b.

Lời giải:

Ta có: a + b > c ⇔ a + b – b > c – b

⇔ a > c – b

Vậy a + b > c khi và chỉ khi a > c – b.

Câu 31: Cho tam giác ABC cân tại A (AB = AC). Gọi M là trung điểm của BC. Chứng minh ΔAMB = ΔAMC.

Lời giải:

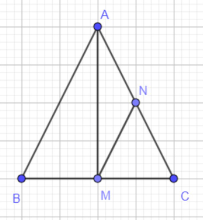
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 62) (ảnh 2)

Xét ΔAMB và ΔAMC có:

AB = AC (do ΔABC cân tại A)

AM cạnh chung

BM = MC (do M là trung điểm của BC)

⇒ ΔAMB = ΔAMC (c.c.c)

Vậy ΔAMB = ΔAMC.

Câu 32: Một công trường dự định phân chia số đất cho 3 đội I, II, III tỉ lệ với 7; 6; 5. Nhưng sau đó vì số người của các đội thay đổi nên đã chia tỉ lệ lại với 6; 5; 4. Như vậy có một đội là nhiều hơn 6 m² đất . Tính số đất đã phân chia cho mỗi đội.

Lời giải:

Gọi số đất đội 1 là a; b; c, đội 2 là x; y; z

Ta có:

$\frac{a}{7} = \frac{b}{6} = \frac{c}{5} (1) \frac{z}{4} = \frac{x}{6} = \frac{y}{5} (2)$

Vì một công trường dự định phân chia số đất cho 3 đội I, II, III tỉ lệ với 7; 6; 5. Nhưng sau đó vì số người của các đội thay đổi nên đẫ chia tỉ lệ lại với 6; 5; 4.

Như vậy có một đội là nhiều hơn 6 m² đất

⇒ (a + b + c) – (x + y + z) = 6

Áp dụng tính chất của dãy tỷ số bằng nhau ta có:

$\frac{(a + b + c) - (x + y + z)}{(7 + 6 + 5) - (6 + 5 + 4)} = 2$

⇒ a = 14; b = 12; c = 10

Vậy số đất đã phân chia cho mỗi đội I; II; III là: 14 m²; 12 m²; 10 m².

Câu 33: Biết đa thức f(x) = x³+ ax² + bx + 2 chia cho x + 1 dư 5, chia cho x + 2 dư 8. Khi đó giá trị của a và b là bao nhiêu?

Lời giải:

Ta có: f(x) = x³+ ax² + bx + 2 chia cho x + 1 dư 5

Suy ra f(x) – 5 chia hết cho x + 1

Hay x³+ ax² + bx + 2 – 5 chia hết cho x + 1

Suy ra x³+ ax² + bx – 3 chia hết cho x + 1

Do đó x = -1 là nghiệm của đa thức f(x)

Khi đó (-1)³ + a(-1)² + b(-1) - 3 = 0

⇒ -1 + a – b – 3 = 0

⇒ a – b = 4 hay b = a – 4

Tương tự ta được f(x) – 8 chia hết cho x + 2

Hay x³+ ax² + bx + 2 – 8 chia hết cho x + 2

Suy ra x³+ ax² + bx – 6 chia hết cho x + 2

⇒ x = –2 là nghiệm của đa thức f(x)

⇒ (–2)³ + a(–2)² + b(–2) – 6 = 0

⇒ –8 + 4a – 2b – 6 = 0

⇒ 4a – 2b = 14

⇒ 2a – b = 7

Thay b = a – 4 vào ta có:

2a – (a – 4) = 7

2a – a + 4 = 7

a + 4 = 7

a = 3

⇒ b = 3 – 4 = –1

Vậy (a; b) = (3; –1)

Câu 34: Biết đa thức f(x) = x³+ ax + b chia cho x – 2 dư 3, chia cho x – 3 dư 5. Tìm đa thức đó.

Lời giải:

Ta có: (x) = x³+ ax + b chia cho x – 2 dư 3

Suy ra f(x) – 3 chia hết cho x – 2

Hay x³+ ax + b – 3 chia hết cho x – 2

Do đó x = 2 là nghiệm của đa thức f(x)

Khi đó 2³ + 2a + b – 3 = 0

⇒ 8 + 2a + b – 3 = 0

⇒ 2a + b = –5 hay b = –2a – 5

Tương tự ta được f(x) – 5 chia hết cho x – 3

Hay x³+ ax + b – 5 chia hết cho x – 3

Do đó x = 3 là nghiệm của đa thức f(x)

⇒ 3³ + 3a + b – 5 = 0

⇒ 27 +3a + b – 5 = 0

⇒ 3a + b = –22

Thay b = –2a – 5 vào ta có:

3a + (–2a – 5) = –22

3a – 2a – 5 = –22

a – 5 = –22

a = –17

⇒ b = (–2)(–17) – 5 = 29

Vậy đa thức f(x) = x³ – 22 + 29.

Câu 35: Cho đường tròn (O; 2cm), các tiếp tuyến AB và AC kẻ từ A đến đường tròn và vuông góc với nhau tại A (B và C là các tiếp điểm). Tứ giác ABOC là hình gì? Vì sao?

Lời giải:

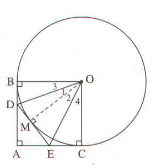
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 62) (ảnh 3)

Xét tứ giác ABOC có: $\hat{A} = \hat{B} = \hat{C} = 90 °$

Suy ra ABOC là hình chữ nhật

Mà AB = AC (tính chất hai tiếp tuyến cắt nhau)

Vậy ABOC là hình vuông.

Câu 36: Cho đường tròn (O; 2cm), các tiếp tuyến AB và AC kẻ từ A đến đường tròn và vuông góc với nhau tại A (B và C là các tiếp điểm). Gọi M là điểm bất kì thuộc cung nhỏ BC. Qua M kẻ tiếp tuyến với đường tròn, cắt AB và AC theo thứ tự tại D và E. Tính chu vi tam giác ADE.

Lời giải:

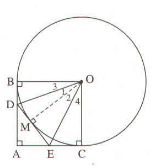
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 62) (ảnh 4)

Theo tính chất hai tiếp tuyến cắt nhau ta có: DB = DM; EM = EC.

Chu vi của tam giác ADE = AD + DE + EA = AD + DM + ME + EA

= AD + DB + AE + EC = AB + AC = 2AB

Xét tứ giác ABOC có: $\hat{A} = \hat{B} = \hat{C} = 90 °$

Suy ra ABOC là hình chữ nhật

Mà AB = AC (tính chất hai tiếp tuyến cắt nhau)

⇒ ABOC là hình vuông

⇒ AB = OB = 2 (cm)

Chu vi của tam giác ADE = 2AB = 2.2 = 4 (cm)

Vậy chu vi của tam giác ADE = 4 cm.

Câu 37: Bác Kim gửi một số tiền vào ngân hàng với lãi suất là 7% và kì hạn là một năm. Sau một năm bác Kim tới ngân hàng rút cả vốn lẫn lãi được 128 400 000 đồng. Hỏi lúc đầu bác Kim gửi vào ngân hàng bao nhiêu tiền?

Lời giải:

Gọi số tiền bác Kim gửi vào ngân hàng là x (đồng) ( $x \in ℕ^{*}$ )

Số tiền lãi sau một năm là:

x.7% = 0,07x (đồng)

Sau một năm bác tới ngân hàng rút là 128 400 000 nên ta có phương trình là:

x + 0,07x = 128 400 000

⇔ 1,07x = 128 400 000

⇔ x = 120 000 000 (TMĐK)

Vậy lúc đầu bác Kim gửi vào ngân hàng 120 000 000 đồng.

Câu 38: Bà Mai vay ngân hàng 200 triệu trong thời gian 2 năm để mở một cửa hàng chuyên sản xuất và bán quà lưu niệm. Theo hợp đồng vay vốn, lãi suất vay trong một năm là 10%. Sau 1 năm, tiền lãi của năm đầu sẽ được cộng vào vốn của năm sau. Hỏi sau 2 năm, Bà Mai phải trả ngân hàng bao nhiêu tiền?

Lời giải:

Số tiền lãi bà Mai phải trả năm đầu là:

200. 10 : 100 = 20 (triệu đồng)

Số tiền bà phải trả cả gốc lẫn lãi năm đầu là: 200 + 20 = 220 (triệu đồng)

Số tiền lãi năm 2 bà Mai phải trả là:

220. 10 : 100 = 22 (triệu đồng)

Số tiền bà Mai phải trả trong 2 năm là:

220 + 22 = 242 (triệu đồng)

Đáp số: 242 triệu đồng.

Câu 39: Cho a, b, c là các số thực dương và thỏa mãn điều kiện abc = 1. Chứng minh $\frac{1}{2 + a} + \frac{1}{2 + b} + \frac{1}{2 + c} \leq 1$ .

Lời giải:

Ta có: $\frac{1}{2 + a} + \frac{1}{2 + b} + \frac{1}{2 + c} \leq 1$

⇔ (b + 2)(c + 2) + (a + 2)(c + 2) + (a + 2)(b + 2) ≤ (a + 2)(b + 2)(c + 2)

⇔ ab +bc + ca + 4(a + b + c) + 12 ≤ abc + 2(ab + bc + ca) + 4(a + b + c) + 8

⇔ ab + bc + ca + 4(a + b + c) + 12 ≤ 1 + 2(ab + bc + ca) + 4(a + b + c) + 8

⇔ ab + bc + ca ≥ 3

Áp dụng bất đẳng thức Cô-si cho 3 số dương ta có:

$a b + b c + c a \geq 3 \sqrt[3]{{(a b c)}^{2}} \geq 3$

Dấu “=” xảy ra khi a = b = c.

Câu 40: Cho hàm số $y = \frac{m x - 2 m - 3}{x - m}$ với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên khoảng (2; +∞). Tìm số phần tử của S.

Lời giải:

Ta có: $y^{'} = \frac{- m^{2} + 2 m + 3}{{(x - m)}^{2}}$

Hàm số đồng biến trên:

(2; +¥) ⇔ y’ > 0, ∀ x ∈ (2; +¥)

$\Rightarrow \{\begin{cases} - m^{2} + 2 m + 3 > 0 \\ x \neq m \in (2; + \infty) \end{cases} \Leftrightarrow \{\begin{cases} - 1 < m < 3 \\ m \leq 2 \end{cases} \Rightarrow - 1 < m \leq 2$