Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 43)

Ngọc Nguyễn Ngày: 13-07-2023 Tổng hợp kiến thức

321

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 43) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 43)

Câu 1: Trung bình cộng của ba số là 13,5, biết tổng của số thứ nhất và số thứ hai là 29,1. Tổng của số thứ hai và số thứ ba là 24,7. Hãy tìm ba số đó.

Lời giải:

Tổng của 3 số là:

13,5 × 3 = 40,5

Số thứ 3 là:

40,5 – 29,1 = 11,4

Số thứ 1 là: 40,5 – 24,5 = 16

Số thứ 2 là: 40,5 – 11,4 – 16 = 13,1

Đáp số: Số thứ nhất:16

Số thứ 2: 13,1

Số thứ 3: 11,4.

Câu 2: Tìm số tự nhiên n sao cho 3n + 13 chia hết cho n + 1.

Lời giải:

Vì 3(n + 1) chia hết cho n + 1 nên để 3n + 13 chia hết cho 1 thì 10 phải chia hết cho n + 1 hay n + 1 là bội ước của 10.

Ta có: 10 = 2 ´ 5 nên các ước của 10 là: Ư(10) = {1; 2; 5; 10}.

Ta có bảng sau:

n + 1	1	2	5	10
n	0	1	4	9
	tmđk	tmđk	tmđk	tmđk

Vậy n ∈{0; 1; 4; 9}.

Câu 3: Tìm số tự nhiên n sao cho 5n + 19 chia hết cho 2n + 1.

Lời giải:

Vì 5n + 19 chia hết cho 2n + 1 nên 2(5n + 19) chia hết cho 2n + 1

Xét 2(5n + 19) = 10n + 38 = 10n = 5 + 33 = 5(2n + 1) + 33

Vì 5(2n + 1) chia hết cho 2n + 1 nên để 2(5n + 19) chia hết cho 2n thì 33 chia hết cho 2n + 1 hay 2n +1 ∈ Ư(33).

Ta có bảng sau:

2n + 1	1	3	11	33
1	0	1	5	16
	tmđk	tmđk	tmđk	tmđk

Vậy n ∈{0; 1; 5; 16}.

Câu 4: Có bao nhiêu số có 4 chữ số được viết từ các chữ số 1; 2; 3; 4; 5; 6; 7; 8; 9 sao cho số đó chia hết cho 15?

Lời giải:

Gọi số cần lập có dạng:

$ℕ = \bar{a b c d} (1 \leq a, b, c, d \leq 9) .$

Ta có: ℕ ⁝ 15

⇒ ℕ ⁝ 3 và ℕ ⁝ 5

+ ℕ ⁝ 5 ⇒ d = 5

+ ℕ ⁝ 3 ⇒ (a + b + c + 5) ⁝ 3

Chọn a có 9 cách chọn, b có 9 cách chọn thì:

+ Nếu a + b + c + 5 chia hết cho 3 thì

c ∈ {3; 6; 9}⇒ c có 3 cách chọn

+ Nếu a + b + c + 5 chia hết cho 3 dư 1 thì:

c ∈ {2; 5; 8}⇒ c có 3 cách chọn

+ Nếu a + b + c + 5 chia hết cho 3 dư 2 thì:

c ∈ {1; 4; 7}⇒ c có 3 cách chọn

Vậy theo quy tắc nhân ta có:

9. 9. 3 = 243 (số)

Đáp số: 243 số

Câu 5: Nhà trường tổ chức giải bóng đá mini mừng xuân cho học sinh khối lớp 8, mỗi lớp cử một đội tham dự, mỗi đội lần lượt thi đấu với đội của lớp bạn một lần.

a) Viết biểu thức đại số tính tổng số trận đấu của khối lớp 8 nếu có x (x ∈ ℤ⁺) đội tham dự.

b) Nếu tổng số trận đấu là 10 thì có bao nhiêu đội tham dự?

Lời giải:

a) Cứ một đội lại đấu với x – 1 đội khác tạo x – 1 trận.

Có tất cả x đội và mỗi trận lặp lại hai lần nên tổng số trận thi đấu là:

$\frac{x (x - 1)}{2}$ (trận)

b) Khi số trận là 10 ta có:

$\frac{x (x - 1)}{2} = 10$

Suy ra x(x – 1) = 20

Suy ra x² – x – 20 = 0

Suy ra x² – 5x + 4x – 20 = 0

Suy ra x(x – 5) + 4(x – 5) = 0

Suy ra (x – 5)(x + 4) = 0

Vì x > 0 nên x + 4 > 0. Do đó: x – 5 = 0

Suy ra x = 5 (tmđk)

Vậy có 5 đội tham dự.

Câu 6: Chứng minh x² – x + 1 > 0 với mọi x.

Lời giải:

$x^{2} - x + 1 = (x^{2} - x + \frac{1}{4}) + \frac{3}{4}$

$= {(x - \frac{1}{2})}^{2} + \frac{3}{4}$

Với mọi giá trị của x ta có:

${(x - \frac{1}{2})}^{2} \geq 0 \Rightarrow {(x - \frac{1}{2})}^{2} + \frac{3}{4} > 0$ (đpcm)

Vậy x² – x + 1 > 0 với mọi x.

Câu 7: Tìm hai số tự nhiên a, b sao cho [a, b] + (a, b) = 55.

Lời giải:

Gọi (a, b) = d, a = dm, b = dn, (m, n) = 1, m, n ∈ ℕ^*

⇒ [a, b] = a . b : (a, b)

Theo đề bài ta có:

[a, b] + (a, b) = 55

Thay vào ta có:

dm.dn : d + d = 55

⇒ d.mn + d = 55

⇒ d(mn + 1) = 55

Vì d, m, n ∈ N*. Giả sử a > b thì m > n, ta có bảng sau:

d	mn + 1	m	n	a	b
1	55	54	1	54 (TM)	1 (TM)
5	11	10	1	50 (TM)	5 (TM)
5	2	25	10	25 (TM)	10 (TM)
11	5	4	1	44 (TM)	11 (TM)

Vậy (a, b) = {(54; 1); (50; 5); (25; 10); (44; 11)}.

Câu 8: Một lớp học có 40 học sinh chia thành các nhóm, mỗi nhóm nhiều nhất 6 học sinh. Hỏi số nhóm ít nhất có thể là bao nhiêu?

Lời giải:

Ta có: 40 : 6 = 6 dư 4

⇒ Có thể xếp 6 nhóm đủ 6 học sinh và thừa 4 học sinh

⇒ Cần số nhóm đủ cho 4 học sinh nữa là: 6 + 1= 7 (nhóm)

Vậy số nhóm ít nhất có thể là 7 nhóm.

Câu 9: Một đội bóng có 45 cầu thủ chia thành các nhóm, mỗi nhóm nhiều nhất 11 cầu thủ. Hỏi số nhóm ít nhất có thể là bao nhiêu?

Lời giải:

Ta có: 65 : 11 = 5 dư 10

⇒ Có thể xếp 5 nhóm đủ 11 cầu thủ và thừa 10 cầu thủ

⇒ Cần số nhóm đủ cho 10 cầu thủ nữa là: 5+1= 6 (nhóm)

Vậy số nhóm ít nhất có thể là 6 nhóm.

Câu 10: Chứng minh rằng: x³+ y³≥ x²y + xy²

Lời giải:

Với x ≥ 0; y ≥ 0 thì x + y ≥ 0

Ta có: x³ + y³ ≥ x²y + xy²

⇔ (x³ + y³) – (x²y + xy²) ≥ 0

⇔ (x + y)(x² – xy + y²) – xy(x + y) ≥ 0

⇔ (x + y)(x² – xy + y² – xy) ≥ 0

⇔ (x + y)(x² – 2xy + y²) ≥ 0

⇔ (x + y)(x – y)² ≥ 0 (Luôn đúng vì x + y ≥ 0 và (x – y)² ≥ 0)

Dấu “ = “ xảy ra khi (x – y)² = 0 ⇔ x = y

Câu 11: Phân tích đa thức thành nhân tử: x³ – x²y – xy² + y³

Lời giải:

Ta có:

x³ – x²y – xy² + y³

= x²(x – y) – y²(x – y)

= (x² – y²)(x – y)

= (x – y)²(x + y)

Câu 12: Một số nếu giảm đi 5 lần rồi bớt đi 32,28 thì được 41,72. Tìm số đó.

Lời giải:

Số đó nếu giảm đi 5 lần thì được số mới là:

41,72 + 32,28 = 74

Số cần tìm là:

74 ´ 5 = 370

Đáp số: 370

Câu 13: Tìm một số biết rằng nếu lấy số đó chia cho 4 rồi cộng với 9 thì được 89.

Lời giải:

Số đó nếu chia cho 4 thì được số mới là:

89 – 9 = 80

Số cần tìm là:

80 ´ 4 = 320

Đáp số: 320

Câu 14: Tính bằng cách thuận tiện:

(1,1 × 1,2 × 1,3 × 1,4 × 1,5 × 1,6) × (1,25 - 0,25 × 5)

Lời giải:

(1,1 × 1,2 × 1,3 × 1,4 × 1,5 × 1,6) × (1,25 - 0,25 × 5)

= (1,1 × 1,2 × 1,3 × 1,4 × 1,5 × 1,6) × (1,25 – 1,25)

= (1,1 × 1,2 × 1,3 × 1,4 × 1,5 × 1,6) × 0 = 0

Câu 15: Tính nhanh:

a) 7,15 : 0,5 + 7,15 × 9 – 7,15;

b) 198 × 27 + 198 × 72 + 198.

Lời giải:

a) 7,15 : 0,5 + 7,15 × 9 – 7,15

= 7,15 × 2 + 7,15 × 9 – 7,15

= 7,15 × (2 + 9 – 1)

= 7,15 × 10

= 71,5.

b) 198 × 27 + 198 × 72 + 198

= 198 × 27 + 198 × 72 + 198 × 1

= 198 × ( 27 + 72 + 1 )

= 198 × 100

= 19800.

Câu 16: Cho hình bình hành ABCD, M và N lần lượt là trung điểm của AB và CD. Chứng minh các tứ giác AMCN là hình bình hành.

Lời giải:

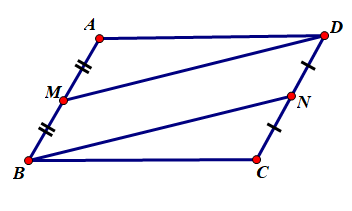
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 43) (ảnh 1)

M là trung điểm của AB nên $A M = M B = \frac{1}{2} A B$

N là trung điểm của CD nên $C N = N D = \frac{1}{2} C D$

Vì ABCD là hình bình hành nên AB = CD và AB // CD

Suy ra $\frac{1}{2} A B = \frac{1}{2} C D$

Hay AM = CN và AM // CN

Suy ra AMCN là hình bình hành.

Vậy AMCN là hình bình hành.

Câu 17: Tìm x, biết:

a) (x – 2)(x – 4) = 0

b) x²(x – 3) = 0

Lời giải:

a) (x – 2)(x – 4) = 0

TH1: x – 2 = 0

x = 0 + 2

x = 2

TH2: x – 4 = 0

x = 0 + 4

x = 4

Vậy $x = \{2; 4\}$

b) x²(x – 3) = 0

TH1: x² = 0

x = 0

TH2: x – 3 = 0

x = 0 + 3

x = 3

Vậy x ∈ {0; 3}.

Câu 18: Phân tích đa thức thành nhân tử:

a) x³ – 2x² – 5x + 6;

b) x⁴ – 16.

Lời giải:

a) x³ – 2x² – 5x + 6

= x³ – x² – x² + 1 – 5x + 5

= x²(x – 1) – (x – 1)(x + 1) – 5(x – 1)

= (x – 1)(x² – x – 1 – 5)

= (x – 1)(x² – x – 6)

= (x – 1)(x² – 3x + 2x – 6)

= (x – 1)[x(x – 3) + 2(x – 3)]

= (x – 1)(x + 2)(x – 3)

b) x⁴ – 16

= (x² – 4)(x² + 4)

= (x – 2)(x + 2)(x² + 4)

Câu 19: 12 người làm xong một công việc trong 4 ngày. Hỏi 16 người làm xong công việc đó trong bao nhiêu ngày? (Biết rằng mức làm của mỗi người như nhau).

Lời giải:

Một người làm xong công việc hết số ngày là:

4 × 12 = 48 (ngày)

16 người làm xong công việc hết số ngày là:

48 : 16 = 3 (ngày)

Đáp số: 3 ngày.

Câu 20: Biết 12 người làm xong một công việc trong 8 ngày. Hỏi muốn làm xong công việc đó trong 3 ngày cần bao nhiêu người? (mức làm mỗi người như nhau).

Lời giải:

Một người làm xong công việc hết số ngày là:

8 × 12 = 96 (ngày)

Số người cần làm xong công việc trong vòng 3 ngày là:

96 : 3 = 32 (ngày)

Đáp số: 32 ngày

Câu 21: Cho biểu thức A = 1 + 3 + 3² + 3³ + 3⁴ + ….+ 3⁹⁹. Chứng minh rằng: A chia hết cho 4.

Lời giải:

Ta có: A = 1 + 3 + 3² + 3³ + 3⁴ + ….+ 3⁹⁹

A = (1 + 3) + (3² + 3³) + …. + (3⁹⁸ + 3⁹⁹)

A = 4 + 3²(1 + 3) + …. + 3⁹⁸(1+3)

A = 4 + 3² × 4 + ….+ 3⁹⁸ × 4

A = 4 × (1 + 3² + …. + 3⁹⁸)

Vậy A chia hết cho 4.

Câu 22: Cho biểu thức B = 1 + 4 + 4² + 4³ + 4⁴ + ….+ 4⁵⁰. Chứng minh rằng: B chia hết cho 21.

Lời giải:

Ta có: B = 1 + 4 + 4² + 4³ + 4⁴ + ….+ 4⁵⁰

B = (1 + 4 + 4²) + (4³ + 4⁴+ 4⁵) + …. + (4⁴⁸ + 4⁴⁹ + 4⁵⁰)

B = (1 + 4 + 4²) + 4³(1 + 4 + 4²) + …. + 4⁴⁸(1 + 4 + 4²)

B = 21 + 21 × 4³ + …. + 21 × 4⁴⁸

B = 21 × (1 + 4³ + …. + 4⁴⁸)

Vậy B chia hết cho 21.

Câu 23: Cho a, b, c là các số hữu tỉ khác 0 tỏa mãn a + b + c = 0. Chứng minh rằng:

$\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}$ là bình phương của một số hữu tỉ.

Lời giải:

$\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} = {(\frac{1}{a} + \frac{1}{b} + \frac{1}{c})}^{2} - 2. (\frac{1}{a b} + \frac{1}{b c} + \frac{1}{c a})$

$= {(\frac{1}{a} + \frac{1}{b} + \frac{1}{c})}^{2} - 2. \frac{a + b + c}{a b c} = {(\frac{1}{a} + \frac{1}{b} + \frac{1}{c})}^{2} - 2. \frac{0}{a b c}$

$= {(\frac{1}{a} + \frac{1}{b} + \frac{1}{c})}^{2}$ (đpcm)

Câu 24: Cho a, b, c là các số hữu tỉ thảo mãn điều kiện ab + bc + ca = 1. Chứng minh rằng biểu thức Q = (a² + 1) (b² + 1) (c² + 1) là bình phương của một số hữu tỉ.

Lời giải:

Thay ab + bc + ca = 1 và Q ta được:

Q = ( a² + ab + ac + bc) (b² + ab + ac + bc) (c² + ab + ac + bc)

= (a + b) (a + c) (b + c) (a + b) (a + c) (b + c)

= [(a + b) (a + c) (b + c)]² là bình phương của một số hữu tỉ (đpcm).

Câu 25: Tìm a, b thuộc Z sao cho a.b = a +b

Lời giải:

Ta có: a.b = a + b nên:

$\begin{array}{l} a . b - a = b \\ \Leftrightarrow a (b - 1) = b \\ \Rightarrow a = \frac{b}{b - 1} = \frac{b - 1 + 1}{b - 1} = \frac{b - 1}{b - 1} + \frac{1}{b - 1} \end{array}$

⇒ b – 1 thuộc Ư(1)

Nếu b – 1 = 1 thì b = 2 suy ra a = 2

Nếu b – 1 = –1 thì b = 0 suy ra a = 0

Vậy (a,b) = (2,2); (0,0)

Câu 26: Tìm tất cả các cặp số nguyên thỏa mãn:

(x – 2019)² = y⁴ – 6y³ + 11y² – 6y

Lời giải:

Biến đổi vế phải ta có:

VP = y⁴ – 6y³ + 11y² – 6y = (y – 1) (y – 2) (y – 3) = (x – 2019)²

⇒ y – 1, y – 3 là 3 số nguyên liên tiếp.

Mà tích của 3 số nguyên liên tiếp không thể là số chính phương

⇒ x – 2019 = 0

y – 1 = 0 hoặc y – 2 = 0 hoặc y – 3 = 0

Vậy ta có các cặp x, y là (2019 : 1) hoặc (2019 : 2) hoặc (2019 : 3).

Câu 27: Tìm a đề hàm số y = log_ax (0 < a khác 1) có đồ thị là hình bên dưới:

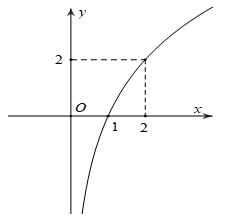
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 43) (ảnh 2)

Lời giải:

Đồ thị hàm số đi qua A(2;2)

⇒ 2 = log_a2

⇒ a²= 2

⇒ $a = \sqrt{2}$

Vậy $a = \sqrt{2}$

Câu 28: Cho đồ thị của ba hàm số y = a^x, y = b^x, y = c^x được vẽ trên cùng một hệ trục toạ độ (như hình vẽ). Chứng minh rằng b > a > c.

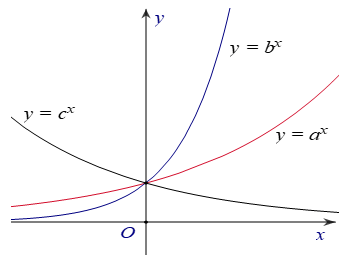
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 43) (ảnh 3)

Lời giải:

Dựa vào đồ thị hàm số ta có:

Do y = a^x và y = b^x là hai hàm đồng biến nên a, b > 1

Do y = c^x nghịch biến nên c < 1.

Suy ra c < a, b

Mặt khác: Lấy x = m, khi đó tồn tại y₁, y₂ > 0 sao cho $\{\begin{matrix} a^{m} = y_{1} \\ b^{m} = y_{2} \end{matrix}$

Dựa vào đồ thị hàm số, dễ thấy y₂ > y₁ hay b^m > a^m

Mà y =a^x và y = b^x là hai hàm đồng biến

Suy ra b > a

Vậy b > a > c

Câu 29: Số dư trong phép chia 1593,48 : 28 là bao nhiêu nếu thương là 56,9.

A. 28

B. 2,8

C. 0,28

D. 0,028

Lời giải:

Đáp án đúng là: C

Số dư là:

1593,48 – 56,9 × 28 = 0,28

Câu 30: Tính giá trị biểu thức bằng cách nhanh nhất, biết rằng x = 3:

A = x(x – 1)(x + 2)(x – 3)(x + 4)(x – 5)

Lời giải:

A = x(x – 1)(x + 2)(x – 3)(x + 4)(x – 5)

Tại x = 3 ta có:

A = 3(3 – 1)(3 + 2)(3 – 3)(3 + 4)(3 – 5)

A = 0 (vì 3 – 3 = 0)

Vậy A = 0

Câu 31: Xác định số dư cảu phép chia 10051,84 : 264 (nếu thương lấy đến 2 chữ số phần thập phân).

Lời giải:

Ta có: 10051,84 : 264 = 1005184 : 26400 = 38,07 (lấy 2 chữ số phần thập phân)

Số dư là:

10051,84 – 38,07 × 264 = 10051,84 – 10050,48 = 1,36

Vậy số dư là 1,36.

Câu 32: Trong mặt phẳng Oxy, cho đường thẳng d: 2x – 5y + 3 = 0. Viết phương trình đường thẳng sao cho d là ảnh của đường thẳng ∆ qua phép quay tâm I (–1; 2), góc quay −180°.

Lời giải:

$Q_{(I; - 180 °)} : Δ \to d$

Phép quay −180° là phép đối xứng tâm nên ∆ và d song song hoặc trùng với nhau

Đặt ∆: 2x − 5y + c = 0

Chọn điểm N (1; 1) ∈ d, tạo ảnh của N là điểm M ∈ ∆

I là trung điểm MN nên:

M (2.(−1) − 1; 2.2 − 1) = (−3; 3)

M ∈ ∆ nên ta có:

− 2.3 − 5.3 + c = 0

− 6 − 15 + c = 0

c = 21

Vậy ∆: 2x − 5y + 21 = 0.

Câu 33: Tâm đường tròn ngoại tiếp hình chữ nhật là gì?

Lời giải:

Giao điểm hai đường chéo hình chữ nhật là trung điểm mỗi đường, mà hai đường chéo hình chữ nhật bằng nhau nên điểm đó sẽ cách đều cả 4 đỉnh của hình chữ nhật hay chính là tâm đường tròn ngoại tiếp hình chữ nhật.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 43) (ảnh 4)

Câu 34: Tìm x, biết 2^x = 64

Lời giải:

2^x = 64

⇔ log₂64 = x

⇔ x = 8

Vậy x = 8.

Câu 35: Tìm x, biết 3^x = 27.

Lời giải:

3^x = 27

log₃27 = x

x = 3

Vậy x = 3.

Câu 36: 260 cm² = ... dm² ... cm².

Lời giải:

260 cm² = 2 dm² 60 cm².

Câu 37: Tìm ba số có trung bình cộng bằng 60, biết rằng nếu viết thêm 1 chữ số 0 vào bên phải số thứ nhất thì được số thứ hai và số thứ ba gấp 4 lần số thứ nhất.

Lời giải:

Vì trung bình cộng ba số là 60 nên tổng ba số là 60 × 3 = 180
Gọi số thứ nhất là a
Theo đề bài:
Nếu viết thêm 1 chữ số 0 vào bên phải số thứ nhất thì được số thứ hai nên số thứ hai gấp 10 lần số thứ nhất
Số thứ hai là: a × 10
Số thứ ba gấp 4 lần số thứ nhất
Số thứ ba là: a × 4
Do đó, ta có: a + a × 10 + a × 4 = 180
a × (1+10+4) = 180
a × 15 = 180
a = 12
Khi đó, số thứ nhất là 12
Số thứ hai là 12 × 10 = 120
Số thứ ba là 12 × 4 = 48
Vậy ba số cần tìm là 12; 120; 48.

Câu 38: Một hình chữ nhật có nửa chu vi là 26 cm, chiều rộng kém chiều dài 8 cm. Tính diện tích của hình chữ nhật đó

Lời giải:

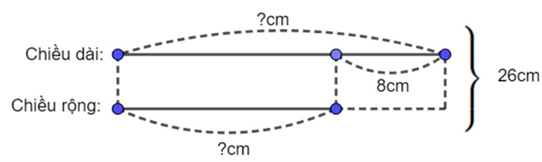
Tổng số đo chiều dài và chiều rộng hình chữ nhật chính bằng nửa chu vi của hình chữ nhật đó: 26 (cm)

Hai lần số đo chiều dài là:

26 + 8 = 34 (cm)

Chiều dài hình chữ nhật là:

34 : 2 = 17 (cm)

Chiều rộng hình chữ nhật là:

17 – 8 = 9 (cm)

Diện tích hình chữ nhật là:

17 × 9 = 153 (cm²)

Đáp số: 153 (cm²)

Câu 39: Cho 31 số nguyên trong đó tổng của 5 số bất kỳ là một số dương. Chứng minh rằng tổng của 31 số đo là số dương.

Lời giải:

Trong 31 số đã cho có ít nhất 1 số là số dương (vì nếu 31 số đã cho đều âm thì tổng của 5 số bất kỳ không thể là 1 số dương).

Tách riêng số dương đó ra còn 30 số, nhóm 5 số vào 1 nhóm thì được 6 nhóm. Trong đó nhóm nào cũng là 1 số dương.

Tổng của 30 số là 1 số dương cộng thêm 1 số dương đã tách.

Vậy tổng của 31 số đó là 1 số dương.

Câu 40: Cho 43 số nguyên, trong đó tổng của 7 số bất kì là một số nguyên âm. Chứng minh rằng tổng của 43 số đó là số nguyên âm.

Lời giải:

Trong 43 số nguyên ta có tổng của 7 số nguyên bất kì là một số nguyên âm nên trong đó có ít nhất một số nguyên âm. Gọi số nguyên âm này là a (a < 0). Còn lại 42 số nguyên nghĩa là có 6 tổng của 7 số nguyên âm bất kì mà tổng 7 số nguyên bất kì là một số nguyên âm nên 6 tổng này cũng là một số nguyên âm.

Vì vậy tổng của 43 số đó là số nguyên âm.

Câu 41: Chọn 4 chữ số khác nhau từ các số 0, 2, 4, 5, 6, 7 để lập thành số có 4 chữ số chia hết cho 5. Hỏi có thể tạo được bao nhiêu số như vậy?

Lời giải:

Có 2 cách chọn hàng đơn vị (0 và 5) Vì số ⋮ 5 cần có tận cùng là 0; 5.

Có 5 cách chọn hàng nghìn.

5 cách chọn hàng nghìn có 4 cách chọn hàng trăm.

4 cách chọn hàng trăm có 3 cách chọn hàng chục.

Vậy tìm được: 2 × 5 × 4 × 3 = 120 (số).

Câu 42: Một người bán một chiếc quạt điện với giá 198 000 đồng thì được lãi 10% tiền vốn một chiếc. Hỏi để lãi 10% giá bán thì người đó phải bán chiếc quạt đó với giá bao nhiêu?

Lời giải:

Lãi 10% tiền vốn là:

198 000 × 10 : 100% = 19 800 (đồng)