Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 82) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 82)
Câu 1: Một cạnh của vật thể dài 20mm, nếu vẽ tỉ lệ 2:1 thì kích thước vẽ trên bản vẽ là bao nhiêu?
Lời giải:
Kích thước vẽ trên bản vẽ là:
20 . 2 = 40 (mm).
Câu 2: Một sân bóng đá hình chữ nhật có diện tích 7140 m2, chiều dài 105m.
a) Tìm chiều rộng của sân bóng đá;
b) Tính chu vi của sân bóng đá.
Lời giải:
a) Chiều rộng của sân bóng là:
7140 : 105 = 68 (m)
b) Chu vi sân bóng đá là:
(105 + 68) . 2 = 346 (m)
Đáp số : a) Chiều rộng: 68 m
b) Chu vi: 346 m.
Lời giải:
Gọi số bút chì màu trong mỗi hộp là x
Vì mỗi hộp có số bút chì màu bằng nhau nên theo bài ra có: 28 chia hết cho x, 36 chia hết cho x.
Hay x ∈ ƯC(28;36)
Ta có: Ư(28) ={1; 2; 4; 7; 14; 28}
Ư(36) = {1; 2; 3; 4; 9; 12; 18; 36}
⇒ ƯC(28,36) = {1; 2; 4}
Mà mỗi hộp đều có số bút chì màu nhiều hơn hai cái
Do đó, mỗi hộp có 4 cái bút chì màu.
Câu 4: Xác định a, b, c biết parabol y = ax2 + bx + c Đi qua ba điểm A(0 ; –1), B(1 ; –1), C(–1; 1).
Lời giải:
(P): y = ax2 + bx + c
Parabol đi qua A(0 ; –1) ⇒ –1 = a.02 + b.0 + c ⇒ c = –1.
Parabol đi qua B(1 ; –1) ⇒ –1 = a.12 + b.1 + c ⇒ a + b + c = –1.
Mà c = –1 ⇒ a + b = 0 (1)
Parabol đi qua C(–1; 1) ⇒ a.(–1)2 + b.(–1) + c = 1 ⇒ a – b + c = 1.
Mà c = –1 ⇒ a – b = 2 (2)
Từ (1) và (2) ⇒ a = 1; b = –1.
Vậy a = 1 ; b = –1 ; c = –1.
Câu 5: Hình chữ nhật ABCD có diện tích 1500 m2. Tính diện tích tam giác AED.
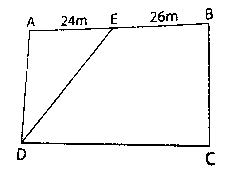
Lời giải:
Chiều dài hình chữ nhật là:
24 + 26 = 50 (m)
Chiều rộng hình chữ nhật là:
1500 : 50 = 30 (m)
Diện tích tam giác là:
30 . 24 : 2 = 360 (m²).
Lời giải:
Số học sinh chỉ giỏi Toán là: 30 – 5 = 25 (học sinh)
Số học sinh chỉ giỏi Văn là: 25 – 5 = 20 (học sinh)
Số học sinh giỏi văn hoặc toán hoặc giỏi cả 2 môn là: 25 + 20 + 5 = 50 (học sinh)
Nhà trường có thể chọn 1 trong 50 bạn trên nên có 50 cách chọn.
Câu 7: Dấu hiệu nhận biết tam giác vuông cân.
Lời giải:
Định nghĩa: Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông của nó bằng nhau hay tam giác cân có một góc vuông.
Dấu hiệu nhận biết tam giác vuông cân là:
- Tam giác vuông có hai cạnh góc vuông bằng nhau.
- Tam giác cân có 1 góc vuông.
Câu 8: Cho hàm số Y = f(x) = 2004x.
a) Chứng minh f(a + b) = f(a) + f(b).
b) Tìm x để f(x) = x2.
Lời giải:
a) Ta cos: f(a) = 2004a; f(b) = 2004b
f(a + b) = 2004(a + b)
f(a) + f(b) = 2004a+ 2004b = 2004(a + b)
Suy ra: f(a + b) = f(a) + f(b)
b) f(x) = x2
Suy ra: 2004x = x2
⇒ x2 – 2004x = 0
⇔ x(x – 2004) = 0
⇔ [x=0x=2004 .
Lời giải:
Sau khi giảm giá của chiếc cặp là:
250000 : 100 . ( 100% – 12% ) = 220000 (đồng).
Lời giải:
Nửa chu vi của mảnh đất hình chữ nhật là:
220 : 2 = 110 (m)
Tổng số phần bằng nhau là:
4 + 7 = 11 (phần)
Chiều rộng của mảnh đất hình chữ nhật là:
110 : 11 . 4 = 40 (m)
Chiều dài của mảnh đất hình chữ nhật là:
110 – 40 = 70 (m)
Diện tích của mảnh đất hình chữ nhật là:
70 . 40 = 2800 (m²)
Diện tích để xây nhà là:
2800 . 10 : 100 = 280 (m²)
Diện tích để làm vườn là:
2800 . 20 : 100 = 560 (m²)
Diện tích để đào ao thả cá là:
2800 – 280 – 560 = 1960 (m²).
Lời giải:
Thời gian xuôi dòng: 2 giờ 24 phút = 2,4 giờ
Độ dài từ A đến B: 2,4 . 18 = 43,2 (km)
Thời gian ngược dòng: 43,2 : 1,8 = 24 (giờ).
Lời giải:
Gọi A là giao điểm của đồ thị (C) với trục tung
Vì A thuộc Oy nên xA = 0
Thay vào ta có: yA = 0 – 2 = – 2
Suy ra: A(0;–2)
Xét: y' = 3x2 – 6x – 3
y'(0) = –3
Phương trình tiếp tuyến của (C) tại điểm A(0;–2) là:
y = y'(0)(x – 0) – 3 = –3x – 2.
Câu 13: Số 2009 có bao nhiêu ước?
Lời giải:
Ta có: 2009 = 72 . 41
Số ước dương của 2009 có dạng 7a.41b
Trong đó a = {0;1;2}, b = {0;1}
a có 3 cách chọn, b có 2 cách chọn
Nên 2009 có số ước dương là: 3.2 = 6 (ước)
Tương ứng với 6 ước dương là 6 ước nguyên âm
Vậy số 2009 có 12 ước.
Câu 14: Tính giá trị của biểu thức:
b) 7 × (48 : 6).
Lời giải:
a) 182 – (96 – 54) = 182 – 42
= 140.
b) 7 × (48 : 6) = 7 × 8
= 56.
Lời giải:
Số lượng nước trong cơ thể người đó là:
70 × 65 : 100 = 45,5 (kg)
Vậy một người 70 kg có khoảng 45,5 kg nước trong cơ thể.
Lời giải:
Ta có: 962 : 58 = 16 (dư 34).
Câu 17: Tính A = 5x(4x2 – 2x + 1) – 2x(10x2 – 5x – 2) với x = 15.
Lời giải:
Ta có:
A = 5x(4x2 – 2x + 1) – 2x(10x2 – 5x – 2)
A = 20x3 – 10x2 + 5x – 20x3 + 10x2 + 4x
A = 9x
Thay x = 15 vào A ta có
A = 9 . 15 = 135
Vậy A = 135 với x = 15.
Lời giải:
Bước 1: Đổ đầy bình 5 lít
Bước 2: Đổ từ bình 5 lít sang bình 3 lít sao cho đầy bình 3 lít, số lít còn lại ở bình 5 lít là 2 lít
Bước 3: Đổ hết rượu từ bình 3 lít trở lại bình 8 lít ban đầu, số lít trong bình ban đầu lúc này là 6 lít
Bước 4: Đổ 2 lít còn lại ở bình 2 lít sang bình 3 lít
Bước 5: Đổ đầy bình 5 lít từ bình ban đầu
Bước 6: Đổ đầy bình 3 lít từ bình 5 lít, số lít còn lại ở bình 5 lít là 4 lít (vì bình 3 lít đã có 2 lít ở bước 4 nên chỉ có thể đổ thêm 1 lít nữa từ bình 5 lít)
Vậy ta lấy được 4 lít rượu.
Lời giải:
Gọi cạnh của vườn rau là a
Suy ra cạnh thửa ruộng hình vuông là 2a
Diện tích vườn rau là: a2
Diện tích thửa ruông hình vuông là: (2a)2 = 4a2
Suy ra diện tích thửa ruộng gấp 4 lần diện tích vườn rau.
Lời giải:
Hai lần xay tất cả số kg thóc là:
165,5 + 134,5 = 300 (kg)
Đổi 300 kg = 3 tạ
Cả hai lần xay được kg gạo là:
67,5 × 3 = 202,5 (kg)
Vậy cả hai lần say được 202,5 kg gạo.
Lời giải:
Diện tích phần tăng lên là:
29,44 – 23,92 = 5,52 (dm)
Chiều rộng hình chữ nhật ban đầu là:
5,52 : 1,2 = 4,6 (dm)
Chiều dài hình chữ nhật ban đầu là:
23,92: 4,6 = 5,2 (dm)
Vậy ban đầu chiều rộng là 4,6 dm và chiều dài là 5,2 dm.
Câu 22: Một hình vuông có cạnh là a. Gọi S là diện tích của hình vuông.

a) Viết công thức tính diện tích của hình vuông đó.
b) Tính diện tích của hình vuông khi a = 25 m.
Lời giải:
a) Muốn tính diện tích hình vuông ta lấy độ dài một cạnh nhân với chính nó nên:
S = a × a.
b) Với a = 25 m thì S = 25 × 25 = 625 (m2).
Câu 23: Tìm số tự nhiên nhỏ nhất có tổng các chữ số của nó là 23.
Lời giải:
Ta có: 23 – 9 – 9 – 5 = 0
Suy ra số nhỏ nhất có tổng các chữ số bằng 23 là 599.
Lời giải:
Một số chia hết cho 3 khi và chỉ khi tổng các chữ số của nó chia hết cho 3
Trong tập hợp {0; 1; 3; 6; 9} có duy nhất số 1 không chia hết cho 3
Vậy số đó chia hết cho 3 khi và chỉ khi các chữ số của nó thuộc tập hợp {0; 3; 6; 9}
Có 4! số có 4 chữ số khác nhau từ {0; 3; 6; 9} (có thể bắt đầu với chữ số 0)
Có 3! số có 4 chữ số khác nhau từ {0; 3; 6; 9} bắt đầu với chữ số 0
Vậy kết quả là có 4! – 3! = 24 – 6 = 18 số.
Câu 25: Tìm x, biết: (x – 5,6) – 3,2 = 4,5.
Lời giải:
(x – 5,6) – 3,2 = 4,5
x – 5,6 = 4,5 + 3,2
x – 5,6 = 7,7
x = 7,7 + 5,6
x = 13,3
Vậy x = 13,3.
Câu 26: Trong số 37 đứa trẻ thì hỏi có bao nhiêu bé chắc chắn sinh cùng tháng?
Lời giải:
Một năm có 12 tháng
Ta có 37 : 12 = 3 dư 1
Suy ra có chắc chắn 3 bé sinh cùng tháng.
Lời giải:
Do trong cà phê tươi, nước chiếm 22% khối lượng nên cà phê nguyên chất chiếm:
100% – 22% = 78%
Đổi 1 tấn = 1000 kg
Khối lượng cà phê nguyên chất có trong 1 tấn cà phê tươi là:
78% × 1000 = 780 (kg)
Trong cà phê khô, nước chiếm 4% khối lượng nên cà phê nguyên chất chiếm
100% − 4% = 96%
Khối lượng cà phê khô (có tỉ lệ nước 4%) là:
780 : 96% = 812,5 (kg)
Khối lượng nước đã bay hơi đi là:
1000 – 812,5 = 187,5 (kg)
Vậy khối lượng nước cần bay hơi đi là 187,5kg để lượng cà phê khô thu được có tỉ lệ nước là 4%.
Lời giải:
Số thuần hạt chiếm số phần trăm trong hạt khô là:
100% – 10 %= 90%
Số thuần hạt chiếm số phần trăm trong hạt tươi là:
100% – 20% = 80%
Số thuần hạt trong hạt khô là:
450 : 100 × 90 = 405 (kg)
Cần phải đem phơi số ki - lô - gam hạt tươi là:
405 : 80 × 100 = 506,25 (kg)
Vậy phơi 506,25 kg hạt tươi được 450 kg hạt khô.
Lời giải:
Số táo của Amy sau khi cho Andy và Johnny giảm là
10 + 7 = 17 (quả)
Số táo của Johnny sau khi nhận thêm táo Amy cho tăng 7 quả
Vì hai bạn có số táo bằng nhau, nên ban đầu Johhny có ít hơn Amy số táo là
17 + 7 = 24 (quả)
Vậy ban đầu Johnny có ít hơn Amy 24 quả táo.
Câu 30: Tổng sau có chia hết cho 3, cho 9 hay không?
1 × 2 × 3 × 4 × 5 × 6 + 27.
Lời giải:
Đặt A = 1 × 2 × 3 × 4 × 5 × 6 + 27
Ta có:
A = 1 × 2 × 3 × 4 × 5 × 6 + 27
A = 2 × 3 × 4 × 5 × 2 × 3 + 9 × 3
A = 2 × 4 × 5 × 2 × 9 + 9 × 3
Suy ra A chia hết cho 9, mà số chia hết cho 9 thì chia hết cho 3
Vậy tổng trên cũng chia hết cho 3 và 9.
Câu 31: Phải pha 3 kg muối với bao nhiêu kg nước để được một bình nước muối chứa 15% muối?
Lời giải:
Khối lượng dung dịch muối sai khi pha là:
3 : 15% = 20 (kg).
Số ki – lô – gam nước cần dùng là:
20 – 3 = 17 (kg)
Vậy cần 17 kg nước để được bình nước muối chứa 15% muối.
Lời giải:
Gọi m (m ∈ ℕ và 200 < m < 400) là số học sinh khối 6 cần tìm.
Vì khi xếp hàng 12, hàng 15, hàng 18 đều dư 5 nên ta có:
m – 5 ⋮ 12; m – 5 ⋮ 15 và m – 5 ⋮ 18
Suy ra m – 5 là bội chung của 12, 15 và 18
Ta có: 12 = 22 . 3; 15 = 3 . 5; 18 = 2 . 32
Suy ra BCNN(12, 15, 18) = 22 . 32 . 5 = 180
Do đó BC(12, 15, 18) = {0; 180; 360; 540; ...}
Suy ra (m – 5) ∈ {0; 180; 360; 540; ...}
Suy ra m ∈ {5; 185; 365; 545; ...}
Mà 200 < m < 400 suy ra m = 365
Vậy số học sinh khối 6 là 365 học sinh.
A. 210;
B. 200;
C. 180;
D. 150.
Lời giải:
Đáp án đúng là: A
Số cách chọn ban thường vụ gồm ba chức vụ bí thư, phó bí thư, ủy viên thường vụ từ 7 người là số các chỉnh hợp chập ba của bảy phần tử
Vậy có A37=210 cách chọn.
Câu 34: Tính bằng cách thuận tiện nhất:
a) 72,64 – (18,35 + 9,29);
b) 45,83 – 8,46 – 7,37.
Lời giải:
a) 72,64 – (18,35 + 9,29)
= 72,64 – 18,35 – 9,29
= 54,29 – 9,29
= 45.
b) 45,83 – 8,46 – 7,37
= 37,37 – 7,37
= 30.
a) A= 1 + 2 + 3 + 4 + ... + 50;
b) B = 2 + 4 + 6 + 8 + ... + 100;
c) C = 1 + 3 + 5 + 7 + ... + 99;
d) D = 2 + 5 + 8 + 11 + ... + 98.
Lời giải:
a) A = 1 + 2 + 3 + 4 + ... + 50
Tổng A có 50 số hạng nên có 25 nhóm 2 số hạng
A = (1 + 50) + (2 + 49) + ... + (25 + 26)
A = 51 + 51 + ... + 51
A = 51 . 25 = 1 275.
b) B = 2 + 4 + 6 + 8 + ... + 100
Số số hạng của tổng B là: (100 – 2) : 2 + 1 = 50 (số)
Do đó B có 25 nhóm 2 số hạng
B = (2 + 100) + (4 + 98) + ... + (50 + 52)
B = 102 + 102 + ... + 102
B = 102 . 25 = 2 550.
c) C = 1 + 3 + 5 + 7 +... + 99
Số số hạng của tổng C là: (99 – 1) : 2 + 1 = 50 (số)
Do đó C có 25 nhóm 2 số hạng
C = (1 + 99) + (3 + 97) +... + (49 + 51)
C = 100 + 100 + ... + 100
C = 100 . 25 = 2 500.
d) D = 2 + 5 + 8 + 11 + ... + 98
Số số hạng của tổng D là: (98 – 2) : 3 + 1 = 33 (số)
Do đó D có 16 nhóm 2 số hạng và lẻ 1 số hạng
D = (2 + 98) + (5 + 95) + ... + (47 + 53) + 50
D = 100 + 100 + ... + 100 + 50
D = 100 . 16 + 50 = 1 650.
Lời giải:
Số thuần hạt chiếm số phần trăm trong hạt khô là:
100% – 10% = 90%
Số thuần hạt chiếm số phần trăm trong hạt tươi là:
100% – 15% = 85%
Số thuần hạt trong hạt khô là:
340 : 100 × 90 = 306 (kg)
Cần phải đem phơi số ki - lô - gam hạt tươi là:
306 : 85 × 100 = 360 (kg)
Vậy phơi 360 kg hạt tươi được 340 kg hạt khô.
A. 128 900 cách;
B. 5 040 cách;
C. 725 760 cách;
D. 144 cách.
Lời giải:
Đáp án đúng là: C
Ta buộc 4 quyển toán với nhau – coi như 1 phần tử, số cách xếp 4 quyển toán này là 4! cách.
Tương tự ta cũng “buộc” 3 quyển sách Lý lại với nhau, thì số cách xếp cho bộ Lý này là 3! cách.
Lúc này ta sẽ đi xếp vị trí cho 7 phần tử trong đó có:
+ 1 buộc Toán
+ 1 buộc Lý
+ 5 quyển Hóa
Thì sẽ có 7! cách xếp
Do đó theo quy tắc nhân ta có 7! × 4! × 3! = 725 760 cách xếp
Vậy ta chọn đáp án C.
Lời giải:
2 lần số bé là:
32 – 2 × 10 = 12
Số bé là:
12 : 2 = 6
Số lớn là:
6 + 20 = 26
Vậy hai số cần tìm là 6 và 26.
Lời giải:
Gọi số hạng thứ nhất và số hạng thứ hai lần lược là a, b
Ta có: a + b = 32
Suy ra a + (b + 7) = 32 + 7 = 39
Vậy tổng mới là 39.
Lời giải:
Gọi A(x0; y0) là điểm nằm trên đường thẳng y = 3x – 7 có hoành độ gấp đôi tung độ
Nên x0 = 2y0
Mà A(x0; y0) nằm trên đường thẳng y = 3x – 7 nên ta có:
y0 = 3 . 2y0 – 7, suy ra 5y0 = 7
Do đó y0=75
Suy ra x0=2.75=145.
Vậy hoành độ của điểm đó là 145.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.