Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23)

Ngọc Nguyễn Ngày: 13-06-2023 Tổng hợp kiến thức

458

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23)

Câu 1: Cho $Δ A B C$ cân tại A.Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho AM + AN = 2AB.

a) Chứng minh rằng: BM = CN

b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN.

c) Đường trung trực của MN và tia phân giác của $\hat{BAC}$ cắt nhau tại K. Chứng minh rằng $ΔBKM = ΔCKN$ từ đó suy ra KC vuông góc với AN

Lời giải:

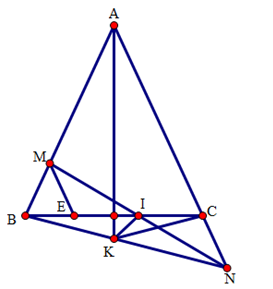
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 2)

a) Do tam giác ABC cân tại A, suy ra AB = AC.

Ta có: AM + AN = AB – BM + AC + CN = 2AB – BM + CN.

Ta lại có AM + AN = 2AB (gt), nên suy ra

2AB – BM + CN = 2AB ⇔ – BM + CN = 0 ⇔ BM = CN.

Vậy BM = CN (đpcm).

b) Gọi I là giao điểm của MN và BC.

Qua M kẻ đường thẳng song song với AC cắt BC tại E.

Do ME // NC nên ta có:

$\hat{M E B} = \hat{A C B}$ (hai góc đồng vị) nên ∆BME cân tại M ⇒ BM = ME mà BM = CN nên ME = CN.

$\hat{CNI} = \hat{IME}$ (hai góc so le trong)

$\hat{MEI} = \hat{NCI}$ (hai góc so le trong)

Ta chứng minh được $ΔMEI = ΔNCI (g . c . g)$

Suy ra MI = NI (hai cạnh tương ứng), từ đó suy ra I là trung điểm của MN.

c) Xét hai tam giác MIK và NIK có:

MI = IN (cmt),

$\hat{MIK} = \hat{NIK} {= 90}^{0}$

IK là cạnh chung. Do đó $ΔMIK = ΔNIK(c.g.c)$

Suy ra KM = KN (hai cạnh tương ứng).

Xét hai tam giác ABK và ACK có: AB = AC(gt), $\hat{BAK} = \hat{CAK}$ (do BK là tia phân giác của $\hat{B A C}$ ), AK là cạnh chung, do đó

Suy ra KB = KC (hai cạnh tương ứng).

Xét hai tam giác BKM và CKN có: MB = CN, BK = KN, MK = KC, do đó

$Δ BKM = Δ CKN(c . c . c)$ suy ra $\hat{MBK} = \hat{KCN}$ .

Mà $\hat{MBK} = \hat{ACK} \Rightarrow \hat{ACK} = \hat{KCN} {= 180}^{0} {: 2 = 90}^{0} \Rightarrow KC ⊥ AN.$ (đpcm)

Câu 2: Tính bằng cách thuận tiện nhất: 34 000 : 125 : 8

Lời giải:

$34000 : (125.8) = 34$

Câu 3: Tính:

372,95 : 3

757,5 : 35

431,25:125

35,1 x 8,5

Lời giải:

372,95 : 3 = 124.316666667

757,5 : 35 = 21.6428571429

431,25:125 = 3.45

35,1 x 8,5 = 298.35

Câu 4: Phân tích thành nhân tử 5(x + 3y) - 15x ( x + 3y )

Lời giải:

5(x + 3y) - 15x ( x + 3y ) = (x + 3y)(5 - 15) = -10(x + 3y)

Câu 5: Cho $Δ$ ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là các điểm đối xứng của H qua các cạnh AB, AC.

a) Chứng minh A, E, D thẳng hàng và BCED là hình thang.

b) Chứng minh $BD . CE = \frac{{DE}^{2}}{4}$ .

c) Cho biết AB = 3cm, AC = 4cm. Tính DE và diện tích $Δ$ DHE.

Lời giải:

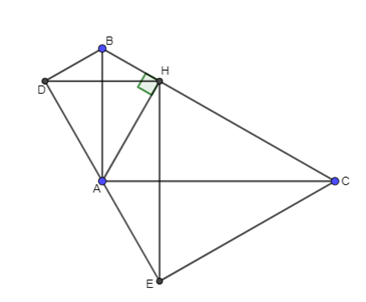
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 3)

a) Do D đối xứng với H qua đoạn AB nên $Δ A D H$ cân tại A

$Δ A D H$ có AB là đường cao đồng thời là phân giác

$\Rightarrow \hat{DAB} = \hat{HAB}$

Tương tự với $Δ A H E \Rightarrow \hat{HAC} = \hat{EAC}$

Ta có :

$\hat{DAE} = (\hat{DAH}) + (\hat{HAE}) = 2. (\hat{BAH}) + 2. (\hat{HAC}) = 2. (\hat{BAH} + \hat{HAC}) = 2.90 = 180$

$\Rightarrow$ D, A, E thẳng hàng

Nhận thấy

$Δ A H C$ đối xứng với $Δ A E C$ qua đoạn thẳng AC $\Rightarrow \hat{AHC} = \hat{AEC} {= 90}^{0}$ (1)

Tương tự , ta cũng có : $\hat{BHA} = \hat{BDA} {= 90}^{0}$ (2)

Từ (1) và (2) $\Rightarrow$ BD // EC (do 2 góc trong cùng phía bù nhau)

b) Ta có : $Δ B H A$ đồng dạng với $Δ A H C$

Suy ra tỷ lệ $\frac{BH}{AH} = \frac{AH}{HC} \Leftrightarrow {AH}^{2} = BH . HC$

Mà BH = BD , HC = CE

$\Rightarrow {AH}^{2} = BD . CE \Leftrightarrow {4AH}^{2} = 4BD . CE$

$\Leftrightarrow {(2AH)}^{2} = 4BD . CE$ (Do AD = AH = AE)

$\Leftrightarrow {DE}^{2} = 4BD . CE$ .

c) Ta có: AD = AH (tính chất đối xứng), AH = AE (tính chất đối xứng)

Suy ra AD = AE mà A, D, E thẳng hàng nên A là trung điểm của DE.

Xét tam giác vuông ABC, vuông tại A, có:

$\frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}} = \frac{1}{3^{2}} + \frac{1}{4^{2}} = \frac{25}{144} \Rightarrow A H = \frac{12}{5}$

$\Rightarrow A D = A E = A H = \frac{12}{5}$

⇒ DE = $\frac{24}{5}$ cm.

Xét tam giác ABC vuông tại A có:

$\tan \hat{A B C} = \frac{A C}{A B} = \frac{4}{3} \Rightarrow \sin \hat{A B C} = \frac{4}{5} \Rightarrow \sin \hat{A D H} = \frac{4}{5}$

Xét tam giác DHE vuông tại H, có:

$\sin \hat{A D H} = \frac{E H}{E D} = \frac{E H}{\frac{24}{5}} = \frac{4}{5} \Rightarrow E H = \frac{96}{25} \Rightarrow D H = \frac{72}{25}$

Vậy diện tích tam giác DEH là: $\frac{1}{2} D H . E H = \frac{1}{2} . \frac{96}{25} . \frac{72}{25} \approx 5,5$ (đvdt).

Câu 6: Cho $Δ A B C$ có A(5; 3); B(2; -1) và C(-1; 5). Tính tọa độ chân đường cao vẽ từ A.

A. (1; 2)

B. ( 1; 1)

C. (1; -1)

D. (-2; 1)

Lời giải:

Chọn B.

Gọi A’(x; y) là tọa độ chân đường cao vẽ từ A;

$\vec{B C} (- 3; 6)$ và $\vec{AA'} (x - 5; y - 3)$

Ta có AA’ và BC vuông góc với nhau nên $\vec{AA'} . \vec{BC} = 0$

Suy ra -3(x - 5) + 6(y - 3) = 0 hay x - 2y + 1 = 0 (1)

Và $\vec{BA'} (x - 2; y + 1); \vec{BC} (-3; 6)$ cùng phương nên 2x + y – 3 = 0 (2)

Từ (1) và (2) suy ra x = y = 1

Vậy điểm A’ cần tìm có tọa độ (1; 1).

Câu 7: Cho tam giác ABC có AB = 3; AC = 5; $\hat{B A C} = 60 ° .$ Gọi M là điểm thuộc đoạn BC sao cho BM = 2MC . Tính độ dài đoạn AM.

Lời giải:

Áp dụng định lý cos, ta có:

$BC = \sqrt{{AB}^{2} {+ AC}^{2} - 2AB . AC . cosBAC} = \sqrt{19} \Rightarrow cosB = \frac{{AB}^{2} {+ BC}^{2} {- AC}^{2}}{2AB . BC} = \frac{\sqrt{19}}{38} BM = 2MC \Rightarrow BM = \frac{2}{3} BC = \frac{2 \sqrt{19}}{3} \Rightarrow AM = \sqrt{{AB}^{2} {+ BM}^{2} - 2AB . BM . cosB} = \frac{\sqrt{139}}{3}$

Câu 8: Cho $Δ A B C$ có AB = 6cm, AC = 3cm, $\hat{B A C} = 60^{0}$ , M là điểm thỏa mãn $\vec{M B} + 2 \vec{M C} = \vec{0}$ . Tính độ dài đoạn AM.

A. $AM = 2 \sqrt{3} cm$

B. $AM = 2 \sqrt{2} cm$

C. $AM = 5cm$

D. $AM = \sqrt{3} cm$

Lời giải:

Áp dụng định lý coscos ta được:

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 4)

Mặt khác:

$\vec{MB} + 2 \vec{MC} \Rightarrow CM = \frac{1}{3} BC = \sqrt{3} cm$

Áp dụng định lý Pytago ta được:

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 5)

Câu 9: Cho $Δ$ ABC có trọng tâm G. Các điểm D, E, F lần lượt là trung điểm của BC, CA, AB và I là giao điểm của AD và EF. Hãy phân tích các vecto AI, AG, DE, DC theo hai vecto AE, AF.

Lời giải:

F là trung điểm AB $\Rightarrow \vec{AF} = \frac{1}{2} \vec{AB}$ ; E là trung điểm AC $\Rightarrow \vec{AE} = \frac{1}{2} \vec{AC}$

Ta có EF song song BC (đường trung bình)

Mà D là trung điểm BC $\Rightarrow$ I là trung điểm EF $\Rightarrow$ AI là trung tuyến

$\Rightarrow \vec{AI} = \frac{1}{2} \vec{AE} + \frac{1}{2} \vec{AF}$

Theo tính chất trọng tâm:

$\vec{AG} = \frac{2}{3} \vec{AD} = \frac{2}{3} (\frac{1}{2} \vec{AB} + \frac{1}{2} \vec{AC}) = \frac{2}{3} (\vec{AE} + \vec{AF}) = \frac{2}{3} \vec{AE} + \frac{2}{3} \vec{AF}$

DE là đường trung bình tam giác ABC

$\Rightarrow \vec{DE} = \frac{1}{2} \vec{BA} = - \frac{1}{2} \vec{AB} = - \vec{AE}$ hay $\vec{DE} = - \vec{AE} + 0 . \vec{AF}$

D là trung điểm BC $\Rightarrow \vec{DC} = \frac{1}{2} \vec{BC}$

$\Rightarrow \vec{DC} = \frac{1}{2} \vec{BA} + \frac{1}{2} \vec{AC} = - \frac{1}{2} \vec{AB} + \frac{1}{2} \vec{AC} = - \vec{AE} + \vec{AF}$

Câu 10: Số lớn nhất có 4 chữ số khác nhau và tích các chữ số bằng 24 là ………

Lời giải:

Tách 24 thành các tích tương ứng gồm các thừa số là số có 1 chữ số:

24 = 6 × 4

24 = 8 × 3

24 = 8 × 3 × 1

24 = 6 × 4 × 1

24 = 4 × 3 × 2 × 1

Số cần tìm là số lớn nhất có 4 chữ số khác nhau nên trong 3 tích vừa tìm được chỉ có tích 4 × 3 × 2 × 1 thỏa mãn yêu cầu Đề bài:

Nên số lớn nhất có 4 chữ số khác nhau và tích các chữ số bằng 24 là 4321

Vậy số cần tìm là 4321

Câu 11: Giải phương trình: $x + \frac{x}{\sqrt{x^{2} -1}} = \frac{35}{12}$

Lời giải:

ĐKXĐ: x > 1 hoặc x < −1

Từ pt $\Rightarrow$ x > 0. Kết hợp vs ĐKXĐ, ta có: x > 1

Pt $\Leftrightarrow x^{2} + \frac{x^{2}}{x^{2} - 1} + \frac{{2x}^{2}}{\sqrt{x^{2} - 1}} = \frac{1225}{144}$

$\Leftrightarrow x^{2} + \frac{x^{2}}{x^{2} - 1} + \frac{{2x}^{2}}{\sqrt{x^{2} - 1}} = \frac{1225}{144}$

Đặt $\frac{x^{2}}{\sqrt{x^{2} - 1}} = y (y > 0)$

Pt trở thành: $y^{2} + 2y = \frac{1225}{144} \Leftrightarrow y = \frac{25}{12}$ (nhận) hoặc $y = \frac{- 49}{12}$ (loại)

$y = \frac{25}{12}$ hay $\frac{x^{2}}{\sqrt{x^{2} - 1}} = \frac{25}{12}$

$\Leftrightarrow \frac{x^{4}}{x^{2} - 1} = \frac{1225}{144} \Leftrightarrow 1 {44x}^{4} {- 625x}^{2} + 625 = 0$

$\Leftrightarrow x = \frac{5}{3}$ hoặc $x = \frac{5}{4}$ (vì x>1x>1)

Câu 12: Cho $\frac{a}{b} = \frac{c}{d}$ . Chứng minh $\frac{2a - 3b}{2a + 3b} = \frac{2c - 3d}{2c + 3d}$

Lời giải:

Đặt $\frac{a}{b} = \frac{c}{d} = k (k \in N^{*})$

$\Rightarrow \{\begin{matrix} a = b k \\ c = d k \end{matrix} \Rightarrow \frac{2 b k - 3 b}{2 b k + 3 b} = \frac{2 d k - 3 d}{2 d k + 3 d}$

Xét vế trái $\frac{2a - 3b}{2a + 3b} = \frac{2bk - 3b}{2bk + 3b} = \frac{b (2k - 3)}{b (2k+3)} = \frac{2k-3}{2k + 3} (1)$

Xét vế phải $\frac{2c - 3d}{2c + 3d} = \frac{2dk - 3d}{2dk + 3d} = \frac{d (2k - 3)}{d (2k+3)} = \frac{2k-3}{2k + 3} (2)$

Từ (1) và (2) ta có Đpcm

Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Lấy điểm I trên đoạn SO sao cho $\frac{S I}{S O} = \frac{2}{3}$ , BI cắt SD tại M và DI cắt SB tại N. MNBD là hình gì ?

A. Hình thang.

B. Hình bình hành.

C. Hình chữ nhật.

D. Tứ diện vì MN và BD chéo nhau.

Lời giải:

Đáp án đúng là: A

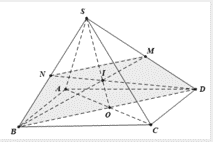
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 6)

+) Tam giác SBD có SO là đường trung tuyến; điểm I nằm trên đoạn SO; $\frac{S I}{S O} = \frac{2}{3}$ .

nên I là trọng tâm tam giác SBD.

⇒ M là trung điểm SD, N là trung điểm SB.

+) Tam giác SBD có MN là đường trung bình nên MN// BD và $M N = \frac{1}{2} S D$

⇒ Nên MNBD là hình thang.

Câu 14: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD với O là giao điểm hai đường chéo AC và BD. Gọi M,N lần lượt là trung điểm các cạnh SA và SD. 1. Chứng minh MO song song với mặt phẳng (SBC) và mặt phẳng (OMN) song song với mặt phẳng (SBC).

2. Gọi K là trung điểm của MO. Chứng minh NK song song với (SBC).

3. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (OMN). Hỏi thiết diện là hình gì ?

Lời giải:

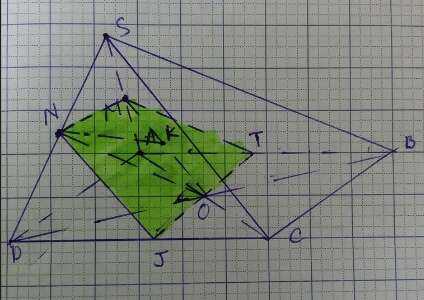
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 7)

1) Ta có: MO là đường trung bình ΔSAC nên MO//SC mà SC⊂(SBC)

Vậy MO//(SBC)

Ta có:

MO//SC

NO//SB

MO, NO⊂(OMN); SC, SB⊂(SBC)

Vậy (OMN)//(SBC)

2) Ta có: (OMN)//(SBC)

Mà NK ⊂ (OMN)

Nên NK//(SBC)

3) Xét (OMN) và (ABCD):

Ta Có:

+) O là điểm chung 1

+) NM//AD (đường TB của tam giác)

Qua O vẽ đường thẳng song song với AD cắt AB tại T, cắt CD tại J

Vậy JT =(OMN) ∩ (ABCD) (1)

(OMN) ∩ (SAD)=MN (2)

(OMN) ∩ (SCD)=NJ (3)

(OMN) ∩ (SAB)=MT (4)

Từ 4 điều trên vậy thiết diện hình thang NMTJ (vì NM//TJ//AD).

Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD.

a) Xác định giao tuyến của hai mặt phẳng (SBD) và (SAC).

b) Gọi K là trung điểm của SD. Tìm giao điểm G của BK với mặt phẳng (SAC); hãy cho biết tính chất của điểm G.

Lời giải:

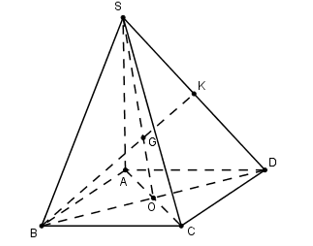
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 8)

a) Gọi $O = AC \cap BD \Rightarrow O \in (SAC) \cap (SBD)$ (1)

Mà $S \in (SAC) \cap (SBD)$ (2)

Từ (1) và (2) $\Rightarrow (SAC) \cap (SBD) =SO$

b) Trong mặt phẳng (SBD) gọi $G = BK \cap SO \Rightarrow G \in SO \subset (SAC)$

$\Rightarrow G = BK \cap (SAC)$

Ta có $G = BK \cap SO$ mà BK và SO là các đường trung tuyến của tam giác SBD

$\Rightarrow$ G là trọng tâm tam giác SBD.

Câu 16: Cho hình thang vuông ABCD có $\hat{A} = \hat{D} {= 90}^{0}$ , $AB = AD = \frac{1}{2} CD$ . Gọi E là trung điểm của CD

a/ Tứ giác ABCE là hình gì?

b/ Tứ giác ABED là hình gì?

c/ Gọi M là giao điểm của AC và BE, K là giao điểm của AE và DM, O là giao điểm hai đuờng chéo hình vuông ABED. Kẻ DH vuông góc với AC cắt AE tại I. Chứng minh DB là tia phân giác của $\hat{I D K}$

d/ Chứng minh BIDK là hình thoi

Lời giải:

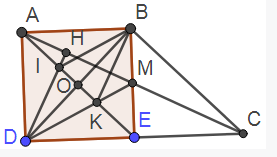
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 9)

a) Xét tứ giác ABCE có AB song song và bằng EC (gt) nên nó là hình bình hành.

b) Xét tứ giác ABED có AB song song và bằng DE (gt) nên nó là hình bình hành.

Lại có $\hat{A D E} = 90^{0}$ nên ABED là hình chữ nhật.

Lại có AB = AD nên ABED là hình vuông.

c) Xét tam giác AME và DMB có :

ME = B

AE = DB (Hai đường chéo hình vuông)

$\hat{A E M} = \hat{D B M} = 45^{0}$ (ABED là hình vuông)

$\Rightarrow Δ A E M = Δ D B M (c - g - c) \to \hat{M A E} = \hat{M D E} (1)$

Xét hai tam giác vuông AHI và DOI có:

$\hat{A I H} = \hat{D I O}$ (Hai góc đối đỉnh)

$\Rightarrow \hat{H A I} = \hat{D I O}$ (Cùng phụ với hai góc bên trên) (2)

Từ (1) và (2) ta có: $\hat{O D K} = \hat{I D O}$ hay DO là tia phân giác của góc $\hat{I D K}$

d) Xét $Δ$ IDK có DO là tia phân giác đồng thời là đường cao nên nó là tam giác cân tại D.Vậy thì DO là đường trung tuyến hay OI = OK.

Do ABED là hình vuông nên O là trung điểm BD.

Xét tứ giác DIBK có O là trung điểm hai đường chéo nên DIBK là hình bình hành.

Lại có $I K ⊥ D B$ nên DIBK là hình thoi.

Câu 17: Cho $Δ$ ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.

Lời giải:

M, N lần lượt là trung điểm AB, AC nên MN là đường trung bình của ABC ứng với cạnh BC

$\Rightarrow MN // BC$ hay $MN // HP$

$\Rightarrow$ MNPH là hình thang (∗)

Mặt khác:
Tam giác vuông ABH có HM là đường trung tuyến ứng với cạnh huyền nên

$HM = \frac{AB}{2} = MB$ (bổ đề quen thuộc)

$\Rightarrow$ MHB cân tại M

$\Rightarrow \hat{MHB} = \hat{MBH}$

Mà $\hat{MBH} = \hat{NPC}$ (hai góc đồng vị với NP // AB)

Hay $\hat{MHP} = \hat{NPH} (**)$

Từ (∗); (∗∗) MNPH là hình thang cân (đpcm)

Câu 18: Cho $Δ$ ABC vuông tại A; đường phân giác BE. Kẻ EH $⊥$ BC (H ∈ BC). Gọi K là giao điểm của AB và HE. Chứng minh rằng:

a) ΔABE = ΔHBE.

b) BE là đường trung trực của đoạn thẳng AH.

c) EK = EC.

d) AE < EC.

Lời giải:

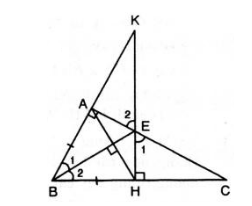
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 10)

a) Xét ΔABE và ΔHBE ta có :

$\hat{B_{1}} = \hat{B_{2}}$

BE là cạnh chung

Do đó $ΔABE = ΔHBE$ (cạnh huyền – góc nhọn).

b) Vì $ΔABE = Δ HBE$ (chứng minh trên)

Suy ra BA = BH, EA = EH (các cặp cạnh tương ứng)

$\Rightarrow$ EB là đường trung trực của AH.

c) Xét $Δ A E K$ và $Δ H E C$ ta có:

AE = EH (chứng minh trên)

$\hat{E_{1}} = \hat{E_{2}}$ (hai góc đối đỉnh).

$\hat{KAE} = \hat{CHE} = 90°$

Do đó $ΔAEK = ΔHEC$ (g.c.g).

Suy ra EK = EC (hai cạnh tương ứng).

d) vuông tại H có EH < EC (do cạnh huyền là lớn nhất trong tam giác vuông).

Mà EH = AE (câu b) nên AE < EC.

Câu 19: Cho $Δ A B C$ vuông tại A điểm M thuộc cạnh BC từ M vẽ các đường thẳng vuông góc với AB ở D vuông góc với AC ở E

a) cm AM = BE.

b) gọi l là điểm đx của D qua A và K là điểm đx của E qua M cm IK, DE, AM đồng quy hai trung điểm O của mỗi đoạn.

c) gọi AH là đường cao của tính số đo $\hat{D H E}$ .

Lời giải:

a) Xét tứ giác ADME có $\hat{DAE} = \hat{ADM} = \hat{AEM} {= 90}^{o}$

$\Rightarrow$ ADME là hình chữ nhật

$\Rightarrow$ AM= DE

b) Gọi O là giao điểm của AM và DE $\Rightarrow$ OA = OM = OD = OE (2)

Do ADME là hình chữ nhật $\Rightarrow$ DA = ME

$\Rightarrow$ 2DA = 2ME hay DA + AI = EM + MK (vì DA = AI; ME = MK)

$\Rightarrow$ DI = EK

Xét tứ giác DIEK có DI = EK (cmt)

DI // EK (vì CEDM là HCN)

$\Rightarrow$ DKEI là hình bình hành

Do O là trung điểm của DE $\Rightarrow$ KI đi qua O

$\Rightarrow$ DE cắt IK tại O và OD = OE; OK = OI (1)

Từ (1) và (2) $\Rightarrow$ DE; AM; IK đồng quy tại trung điểm O của mỗi đường

c) Xét AHM vuông tại H có O là trung điểm của AM, khi đó HO là đường trung tuyến ứng với cạnh huyền AM. Suy ra $HO = \frac{1}{2} . AM$

Mặt khác, AM = DE.

$\Rightarrow HO = \frac{1}{2} . DE$

Xét DHO có đường trung tuyến $HO = \frac{1}{2} . DE$

$\Rightarrow$ DHE vuông tại H $\Rightarrow \hat{DHE} {= 90}^{o}$

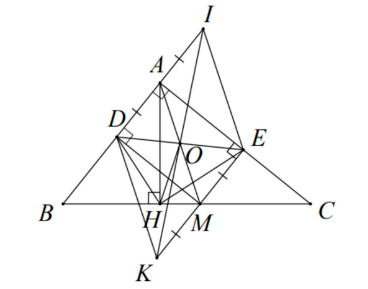
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 11)

Câu 20: Cho tứ giác ABCD có AC cắt BD tại O, $\hat{A B D} = \hat{A C D}$ . Gọi E là giao điểm của AD và BC CMR :

a) Các tam giác AOB và DOC đồng dạng.

b) Các tam giác AOD và BOC đồng dạng.

c) EA . ED = EB . EC.

Lời giải:

a) Xét $Δ A O B$ và $Δ D O C$ có:

$\hat{A O B} = \hat{C O D}$

$\hat{A B D} = \hat{A C D}$

do đó : $Δ A O B$ đồng dạng với $Δ D O C$ (g-g)

b) theo cm câu a: $Δ A O B$ đồng dạng với $Δ D O C$

$\Rightarrow \frac{AO}{OD} = \frac{OB}{OC}$

Xét $Δ A O D$ và $Δ B O C$ có:

$\frac{OA}{OD} = \frac{OB}{OC}$

$\hat{AOD} = \hat{BOC}$ (2 góc đối đỉnh)

Do đó: $Δ A O D$ đồng dạng với $Δ B O C$ (c-g-c)

c) Xét $Δ D B E$ và $Δ C A E$ có:

$\hat{D E C}$ chung

$\hat{EDB} = \hat{ACE}$ ( 2 góc tương ứng của $Δ A O D$ đồng dạng với $Δ B O C$ )

Do đó: $Δ D B E$ đồng dạng với $Δ C A E$ (g - g)

$\Rightarrow \frac{EB}{EA} = \frac{ED}{EC} \Rightarrow EA . ED = EB . EC$

Câu 21: Anh Long đi taxi từ nhà đến ga tàu hết 35.000 đồng, biết rằng đoạn đường từ nhà anh long đến ga là 2,5 km. Hỏi trung bình đi mỗi km bằng taxi anh Long phải trả bao nhiêu tiền ?

Lời giải:

Trung bình đi mỗi km bằng số tiền anh Long phải trả:

$35000 : 2,5 = 14000$ (đồng)

Câu 22: Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có: $\vec{M A} + \vec{M C} = \vec{M B} + \vec{M D}$

Lời giải:

Do ABCD là hình bình hành nên $\vec{A B} = \vec{D C}$

$\begin{array}{l} \Rightarrow \vec{A M} + \vec{M B} = \vec{D M} + \vec{M C} \\ \Leftrightarrow - \vec{M A} + \vec{M B} = - \vec{M D} + \vec{M C} \\ \Leftrightarrow \vec{M A} + \vec{M C} = \vec{M B} + \vec{M D} \end{array}$

Cách 2:

Ta có:

$\vec{M A} + \vec{M C} = \vec{M B} + \vec{M D} \Leftrightarrow \vec{M A} - \vec{M B} = \vec{M D} - \vec{M C}$

Áp dụng quy tắc hiệu ta có: $\vec{M A} - \vec{M B} = \vec{B A}; \vec{M D} - \vec{M C} = \vec{C D}$

Câu 23: Chứng minh với mọi x thuộc N, $x^{2} + 1$ không chia hết cho 3.

Lời giải:

Giả sử $x^{2} + 1$ chia hết cho 3

$\Rightarrow x^{2} + 1 \in B_{(3)} \Rightarrow x^{2} + 1 \in \{\pm 3, \pm 6, \pm 9, \pm 12, \pm 15,....\} \Rightarrow x^{2} \in \{2, - 4,5, - 7,8, - 10,....\}$

Mà $x \in N$

$\Rightarrow x^{2} \in \{2,5,8,11,14,...\} \Rightarrow x \in \{\sqrt{2}, \sqrt{5}, \sqrt{8},...\}$

Mà $x \in N$

$\Rightarrow x \in \{\emptyset\}$

Vậy không tồn tại x để $x^{2} + 1$ chia hết cho 3 hay $x^{2} + 1$ không chia hết cho 3 với mọi $x \in N$ .

Câu 24: Tổng 2 số lẻ là 884. Tìm 2 số, biết rằng giữa chúng có 7 số chẵn liên tiếp nữa ?

Lời giải:

Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị, còn hai số chẵn liên tiếp hơn kém nhau 2 đơn vị.
Số lớn hơn số bé là:
1 x 2 + 2 x 6 = 14
Số lớn là:
( 884 + 14 ) : 2 = 449
Số bé là:
884 - 449 = 435
Vậy hai số lẻ phải tìm là 435 và 449

Câu 25: Tìm hai số lẻ biết tổng của chúng là 50 và giữa chúng có ba số lẻ khác.

Lời giải:

Gọi a là số lẻ thứ nhất

Giữa số lẻ thứ nhất và thứ hai có 3 số khác lần lượt là

a + 2; a + 4; a + 6 và số lẻ cần tìm là a + 8

Tổng của chúng là 50 nên ta có

a + a + 8 = 50

→ 2a = 42

→ a = 21

Vậy 2 số lẻ cần tìm là 21 và 29

Câu 26: Cho nửa đường tròn (O) đường kính AB = 2R. Vẽ đường thẳng d là tiếp tuyến của (O) tại B. Trên cung AB lấy điểm M tùy ý tia AM cắt d tại N. Gọi C là trung điểm của AM tia CO cắt d tại D.

a ) CMR OBNC nội tiếp.

b ) CMR NO vuông góc với AD.

c ) CMR CA . CN = CO . CD

d ) Xác định vị trí điểm M để (2AM + AN ) đạt GTNN.

Lời giải:

Câu a) Ta có: cân tại O và AC = MC nên $O C ⊥ A M$ hay $\hat{O C N} = 90^{0}$ .

Xét tứ giác OBNC ta có :

$\hat{O C N} = 90^{0}$ ( cmt )

$\hat{O B N} = 90^{0}$ ( Tiếp tuyến vuông góc với bán kính )

$\Rightarrow \hat{O C N} + \hat{O B N} = 180^{0}$ hay OBNC là tứ giác nội tiếp (đpcm )

Câu b ) Xét tam giác AND ta có :

AB là đường cao xuất phát từ đỉnh A.

DC là đường cao xuất phát từ đỉnh D.

Mà hai đường cao này cắt nhau tại O cho nên O là trực tâm của

NO cắt AD suy ra NO là đường cao của tam giác AND $\Rightarrow N O ⊥ A D$

Câu c ) Ta có

$\{\begin{matrix} \hat{C A O} + \hat{A N B} = 90^{0} \\ \hat{C D N} + \hat{A N B} = 90^{0} \end{matrix} \Rightarrow \hat{C A O} = \hat{C D N}$

Xét tam giác CAO và tam giác CDN ta có :

$\{\begin{matrix} \hat{A C O} = \hat{D C N} (= 90^{0}) \\ \hat{C A O} = \hat{C D B} (c m t) \end{matrix}$

$\Rightarrow Δ C A O ~ Δ C D N (g - g)$

$\Rightarrow \frac{C A}{C D} = \frac{C O}{C N} \Rightarrow C A . C N = C O . C D$ ( đpcm )

Câu d ) Xét tam giác AMB và tam giác ABN ta có :

$\{\begin{matrix} \hat{B A M} : c h u n g \\ \hat{A M B} = \hat{A B N} (= 90^{0}) \end{matrix}$

$\Rightarrow Δ A M B ~ Δ A B N (g - g) \Rightarrow \frac{A M}{A B} = \frac{A B}{A N} \Rightarrow A M . A N = A B^{2} = 4 R^{2}$

Áp dụng BĐT cô – si ta có:

$2 A M + A N \geq 2 \sqrt{2 A M . A N} = 2 \sqrt{8 R^{2}} = 4 R \sqrt{2}$

Vậy GTNN của 2AM + AN là $4 R \sqrt{2}$ khi và chỉ khi M là trung điểm của AN

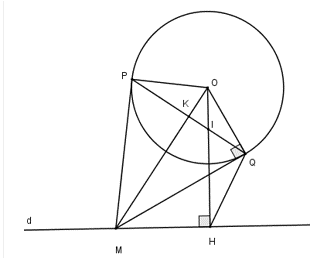
Câu 27: Cho đường tròn tâm O bán kính R và một đường thẳng d cố định không giao nhau. Hạ OH vuông góc với d. M là một điểm tùy ý trên d (M không trùng với H). Từ M kẻ hai tiếp tuyến MP và MQ với đường tròn (O; R) (P, Q là các tiếp điểm và tia MQ nằm giữa hai tia MH và MO). Dây cung PQ cắt OH và OM lần lượt tại I và K.

1) Chứng minh rằng tứ giác OMHQ nội tiếp.

2) Chứng minh rằng $\hat{O M H} = \hat{O I P}$

3) Chứng minh rằng khi M di chuyển trên đường thẳng d thì điểm I luôn cố định.

4) Biết $O H = R \sqrt{2}$ , tính IP . IQ.

Lời giải:

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 12)

1) Xét tứ giác OMHQ có $\hat{O Q M} = 90^{0}$ (MQ là tiếp tuyến của (O))

$\hat{O H M} = 90^{0}$ ( $O H ⊥ d$ )

Vậy tứ giác OMHQ nội tiếp (Tứ giác có hai góc nội tiếp bằng nhau)

2) Ta có: $\hat{O M H} + \hat{M O H} = 90^{0}$ (tổng hai góc nhọn trong tam giác vuông OMH)

Ta có OP = OQ = R, MP = MQ (tính chất hai tiếp tuyến cắt nhau)

→ OM là trung trực của PQ $\to O M ⊥ P Q$

$\to \hat{O I P} + \hat{M O H} = 90^{0}$ (tổng hai góc nhọn trong tam giác vuông OIK)

Vậy $\hat{O M H} = \hat{O I P}$ (cùng phụ với $\hat{M O H}$ )

3) Xét hai tam giác OIK và OMH có $\hat{O M H} = \hat{O I P}$ (cmt), $\hat{O H M} = \hat{O K I} = 90^{0}$

Suy ra $Δ O I K ~ Δ O M H$ (g.g)

$\to \frac{O I}{O M} = \frac{O K}{O H} \to O I = \frac{O K . O M}{O H}$

Áp dụng hệ thức lượng trong tam giác vuông OQM có $R^{2} = O Q^{2} = O K . O M$

$\to O I = \frac{R^{2}}{O H}$

Vì d cố định nên OH không đổi, R luôn không đổi nên OI không đổi. Mà $I \in O H$ cố định nên I cố định.

4) Xét tứ giác OPMQ có:

$\hat{O P M} + \hat{O Q M} = 180^{0} \to$ Tứ giác OPMQ nội tiếp (Tứ giác có tổng hai góc đối bằng $180^{0}$ )

$\to \hat{O P I} = \hat{O M Q}$ (hai góc nội tiếp cùng chắn cung OQ)

Câu 28: Một vật hình hộp chữ nhật có kích thước 30 . 20 . 10 (cm)

Ta thả ''nằm'' vật vào bình trụ đựng nước

a) Thể tích phần chòm của vật là bao nhiêu? Chiều cao phần vật chìm trong nước là mấy ?

b) Nếu ta đổ dầu vào cho vật ngập hoàn toàn thì thể tích vật ngập trong nước có thay đổi không ?

c) Lượng dầu đổ vào tối thiểu là mấy biết diện tích đáy bình trụ là 20dm^{2 .}cho biết trọng lượng riêng nước, dầu, vật lần lượt là 10000N/m³; 8000N/m³; 9000N/m³ ?

Lời giải:

a) Thả nằm tức là áp mặt 30 . 20 xuống nước. Gọi h_c là chiều cao phần chìm.

$\begin{array}{l} V = 0,3.0,2.0,1 = 0,006 (m^{3}) \\ S = 0,3.0,2 = 0,06 (m^{2}) \end{array}$

Khi khối gỗ cân bằng:

$F_{A} = P \Rightarrow d_{n} . V_{c} = d_{v} . V \Rightarrow d_{n} .0,06. h_{c} = d_{v} .0,006 \Rightarrow d_{n} .10 h_{c} = d_{v} \Rightarrow h_{c} = \frac{d_{v}}{d_{n} .10}$

Thay số vào tính được h_c = 0,09m = 9cm.

b) Gọi h' là chiều cao phần gỗ ngập dầu. Khi khối gỗ cân bằng ta có:

$\begin{array}{l} P = F_{A'} + F_{A 1} \\ \Rightarrow d_{v} . S . h = d_{d} . S . h' + d_{n} . S . (h - h') \\ \Rightarrow d_{v} . h = d_{d} . h' + d_{n} . h - d_{n} . h' \\ \Rightarrow d_{v} . h = h' (d_{d} - d_{n}) + d_{n} . h \\ \Rightarrow h' = \frac{d_{v} . h - d_{n} . h}{d_{d} - d_{n}} \end{array}$

(h = 0,1m)

Thay số vào tính được h' = 0,05m = 5cm.

c) Độ cao dầu tối thiểu phải rót vào là 5cm . 20dm³ = 0,02m³

Thể tích dầu tối thiểu phải rót vào:

$V_{d} = S' . h' = 0,02.0,005 = 0,0001 (m^{3}) = 100 (c m^{3})$

Câu 29: Một hình hộp chữ nhật có chiều dài 20 cm, chiều rộng 15 cm, chiều cao 10 cm. Bạn Bình dán giấy màu đỏ vào các mặt xung quanh và giấy màu vàng vào hai mặt bên cái hộp đó chỉ dán mặt ngoài. Hỏi diện tích tích giấy màu nào lớn hơn và lớn hơn bao nhiêu cm²?

Lời giải:

Diện tích mặt xung quanh hay diện tích dán giấy màu đỏ là:

$(20 + 15) \times 2 \times 10 = 700$ (cm²)

Diện tích hai mặt đáy hay diện tích dán giấy màu vàng là:

$20 \times 15 \times 2 = 600$ (cm²)

Diện tích giấy màu đỏ lớn hơn số (cm²) là:

$700 - 600 = 100$ (cm²)

Đáp số: 100 cm²

Câu 30: Tìm số nguyên tố p sao cho p + 8 và p + 16 đều là các số nguyên tố.

Lời giải:

Trường hợp 1: p = 3

→ p + 8 = 11 và p + 16 = 19(nhận)

Trường hợp 2: p = 3k + 1

→ p + 8 = 3k + 9 (loại)

Trường hợp 3: p = 3k + 2

→ p + 16 = 3k + 18(loại)

Câu 31: Công thức tính số tổ hợp là:

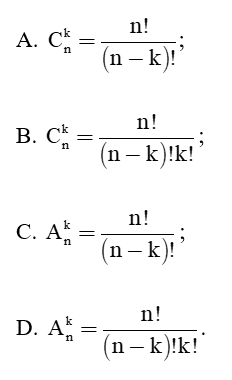
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 13)

Lời giải:

Đáp án đúng là: A.

Số các tổ hợp chập k của một tập hợp n phần tử, kí hiệu là $C_{n}^{k}$ và được cho bởi công thức: $C_{n}^{k} = \frac{n!}{k (n - k)!}$ .

Câu 32: Phân tích đa thức thành nhân tử: x⁸ + x⁷ + 1.

Lời giải:

x⁸ + x⁷ + 1 = (x⁸ – x²) + (x⁷ – x) + x² + x + 1

= x²(x⁶ – 1) + x(x⁶ – 1) + x² + x + 1

= x(x + 1)(x⁶ – 1) + (x² + x + 1)

= x(x + 1)(x³ – 1)(x³ + 1) + (x² + x + 1)

= x(x + 1)(x – 1)(x³ + 1)(x² + x + 1) + (x² + x + 1)

= (x² + x + 1)[(x³ – x)(x³ + 1) + 1]

= (x² + x + 1)(x⁶ – x⁴ + x³ – x +1).

Câu 33: Gọi a, b, c lần lượt là ba cạnh của tam giác; h_a, h_b, h_c lần lượt là các đường cao tương ứng với ba cạnh đó và r là bán kính đường tròn nội tiếp tam giác đó. Chứng minh rằng: $\frac{1}{h_{a}} + \frac{1}{h_{b}} + \frac{1}{h_{c}} = \frac{1}{r}$ .

Lời giải:

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 14)

Ta có:

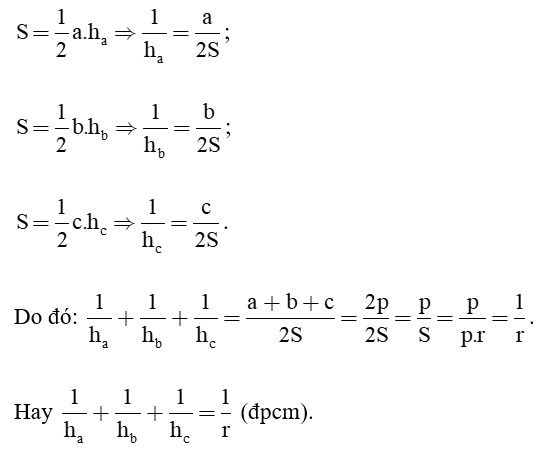
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 15)

Câu 34: Phân tích đa thức x⁵ + x + 1 thành nhân tử.

Lời giải:

x⁵ + x + 1 = x⁵ – x² + x² + x + 1

= x²(x³ – 1) + (x² + x + 1)

= x²(x – 1)(x² + x + 1) + (x² + x + 1)

= (x² + x+ 1)[x²(x – 1) + 1]

= (x² + x + 1)(x³ – x² + 1).

Câu 35: Ông và bà An cùng có 6 đứa con đang lên máy bay theo một hàng dọc. Có bao nhiêu cách xếp hàng khác nhau nếu ông hay bà An đứng ở đầu hoặc cuối hàng.

A. 720;

B. 1440;

C. 18 720;

D. 40 320.

Lời giải:

Đáp án đúng là: B

• TH1. Ông An đứng ở đầu hàng, bà An đứng ở cuối hàng và 6 người con đứng ở giữa.

Khi đó có tất cả 6! cách sắp xếp.

• TH2. Ông An đứng ở cuối, bà An đứng ở đầu hàng và 6 người con đứng ở giữa.

Khi đó có tất cả 6! cách sắp xếp.

Số cách xếp hàng khác nhau nếu ông hay bà An đứng ở đầu hoặc cuối hàng là:

2 . 6! = 2 . 720 = 1 440 (cách)

Vậy có 1 440 cách cần tìm.

Câu 36: Tìm số nguyên tố x, y thỏa mãn x² – 2y² = 1.

Lời giải:

Ta có: x² – 2y² = 1 ⇔ x² = 2y² + 1; $y^{2} = \frac{x^{2} - 1}{2}$ .

Suy ra x² là một số chính phương lẻ, x là số lẻ.

Đặt x = 2k + 1 (k nguyên dương).

Ta có $y^{2} = \frac{{(2 k + 1)}^{2} - 1}{2} = \frac{4 k^{2} + 4 k}{2} = 2 k (k + 1)$ (*)

Y là một số nguyên tố nên y² sẽ là một số nguyên dương mà có duy nhất 3 ước là {1; y; y²}.

Từ (*) dễ thấy $y^{2} ⋮ 2$ và do y là số nguyên tố nên suy ra y = 2 $\Rightarrow$ k = 1 $\Rightarrow$ x = 3.

Vậy x = 3 và y = 2 thỏa mãn yêu cầu bài toán.

Câu 37: Tổng tất cả các ước của 4 là:

A. –7;

B. 4;

C. 0;

D. 7.

Lời giải:

Đáp án đúng là: C.

Ước của 4 gồm các số: –4; –2; –1; 1; 2; 4.

Tổng các ước của 4 là:

−4 – 2 – 1 + 1 + 2 + 4 = (4 – 4) + (2 – 2) + (1 – 1) = 0.

Vậy tổng các ước của 4 là 0.

Câu 38: Tìm x, biết: 4x² – 25 – (2x – 5)(2x + 7) = 0.

Lời giải:

4x² – 25 – (2x – 5)(2x + 7) = 0

⇔ (4x² – 25) – (2x – 5)(2x + 7) = 0

⇔ (2x – 5)(2x + 5) – (2x – 5)(2x + 7) = 0

⇔ (2x – 5)(2x + 5 – 2x – 7) = 0

⇔ (2x – 5).(–2) = 0

⇔ 2x – 5 = 0

⇔ $x = \frac{5}{2}$

Vậy $x = \frac{5}{2}$ .

Câu 39: Tìm x biết 8x³ – 12x² + 6x – 1 = 0.

Lời giải:

8x³ – 12x² + 6x – 1 = 0

⇔ (2x)³ – 3. (2x)². 1 + 3. 2x . 1² – 1³ = 0

⇔ (2x – 1)³ = 0

⇔ 2x – 1 = 0

⇔ $x = \frac{1}{2}$ .

Câu 40: Tìm giá trị y thỏa mãn 49(y – 4)² – 9(y + 2)² = 0.

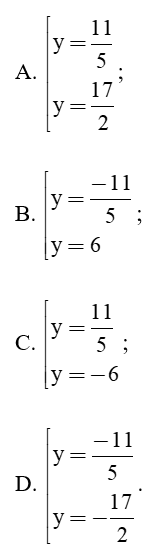
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 16)

Lời giải:

Đáp án đúng là: A

Ta có 49(y – 4)² − 9(y + 2)² = 0

⇔ 49(y² − 8y + 16) − (y² + 4y + 4) = 0

⇔ 49y² − 392y + 784 – 9y² − 36y − 36 = 0

⇔ 40y² − 428y + 748 = 0

⇔ 4(y² − 107y + 187) = 0

⇔ 4[(10y² − 22y) − ( 85y − 187)] = 0

⇔ 4[2y(5y − 11) − 17(5y − 11)] = 0

⇔ 4(5y − 11)(2y − 17) = 0

$\Leftrightarrow [\begin{array}{l} 5 y - 11 = 0 \\ 2 y - 17 = 0 \end{array} \Leftrightarrow [\begin{array}{l} y = \frac{11}{5} \\ y = \frac{17}{2} \end{array}$

Câu 41: Rút gọn: A = x(5x – 3) – x²(x – 1) + x(x² – 6x) – 10 + 3x.

Lời giải:

A = x(5x – 3) – x²(x – 1) + x(x² – 6x) – 10 + 3x

= 5x² – 3x – x³ + x² + x³ – 6x² – 10 + 3x = −10.

Câu 42: Cho hai tập hợp khác rỗng: A = (m – 1; 4], B = (−2; 2m + 2), với m ∈ ℝ. Xác định m để:

a) A ∩ B = Ø;

b) A ⊂ B;

c) B ⊂ A;

d) (A ∩ B) ⊂ (−1; 3).

Lời giải:

Với A = (m – 1; 4], B = (−2; 2m + 2) là các tập khác tập rỗng, ta có điều kiện:

$\{\begin{cases} m - 1 < 4 \\ 2 m + 2 > - 2 \end{cases} \Leftrightarrow \{\begin{cases} m < 5 \\ m > - 2 \end{cases}$ ⇔ −2 < m < 5 (*)

a) Ta có: A ∩ B = Ø ⇔ m – 1 < 2m + 2 ⇔ m > −3.

So sánh với điều kiện (*) ta thấy các giá trị m thỏa mãn yêu cầu là: −2 < m < 5.

b) A ⊂ B $\Leftrightarrow \{\begin{cases} m - 1 \geq - 2 \\ 2 m + 2 > 4 \end{cases} \Leftrightarrow \{\begin{cases} m \geq - 1 \\ m > 1 \end{cases} \Leftrightarrow m > 1$ .

So sánh với điều kiện (*) ta có các giá trị thỏa mãn yêu cầu bài toán là: 1 < m < 5.

c) B ⊂ A $\Leftrightarrow \{\begin{cases} m - 1 \leq - 2 \\ 2 m + 2 \geq 4 \end{cases} \Leftrightarrow \{\begin{cases} m \leq - 1 \\ m \leq 1 \end{cases} \Leftrightarrow m \leq 1$ .

So sánh với (*) ta thấy các giá trị m thỏa mãn yêu cầu bài toán là: −2 < m ≤ −1.

d) (A ∩ B) ⊂ (−1; 3) $\Leftrightarrow \{\begin{cases} m - 1 \geq - 1 \\ 2 m + 2 \leq 3 \end{cases} \Leftrightarrow 0 \leq m \leq \frac{1}{2}$ (*).

Vậy với $0 \leq m \leq \frac{1}{2}$ thoản mãn yêu cầu bài toán.

Câu 43: Phân tích đa thức thành nhân tử: A = ab(a + b) – bc(b + c) + ac (a – c).

Lời giải:

A = ab(a + b) – bc(b + c) + ac (a – c)

= a²b + ab² – b²c – bc² + a²c – ac²

= (a²b + a²c) + (ab² – ac²) – (b²c + bc²)

= a²(b + c) + a(b² – c²) – bc(b + c)

= a²(b + c) + a(b + c)(b – c) – bc(b + c)

= (b + c)[a² + a(b – c) − bc]

= (b + c)(a² + ab – ac − bc)

= (b + c)[a(a + b) – c (a + b)]

= (b + c)(a + b)(a – c).

Câu 44: Cho x, y, z > 0 thỏa mãn x + y + z = 1. Tìm giá trị lớn nhất của

$Q = \frac{x}{x + \sqrt{x + y z}} + \frac{y}{y + \sqrt{y + z x}} + \frac{z}{z + \sqrt{z + x y}}$ .

Lời giải:

Ta có: x + yz = x(x + y + z) + yz

= x² + yz + x(y + z) = A

Áp dụng bất đẳng thức Cô-si ta có:

A $\geq 2 x \sqrt{y z} + x (y + z) (x^{2} + y z \geq 2 \sqrt{x^{2} y z}) = x {(\sqrt{y} + \sqrt{z})}^{2}$ .

Hay $x + y z \geq x {(\sqrt{y} + \sqrt{z})}^{2}$ .

Tương tự ta có: $y + z x \geq y {(\sqrt{z} + \sqrt{x})}^{2}$ ;

$z + x y \geq z {(\sqrt{x} + \sqrt{y})}^{2}$ .

Khi đó ta có:

$P \leq \frac{x}{x + \sqrt{x {(\sqrt{y} + \sqrt{z})}^{2}}} + \frac{y}{y + \sqrt{y {(\sqrt{z} + \sqrt{x})}^{2}}} + \frac{z}{z + \sqrt{z {(\sqrt{x} + \sqrt{y})}^{2}}}$

$= \frac{\sqrt{x}}{\sqrt{x} + \sqrt{y} + \sqrt{z}} + \frac{\sqrt{y}}{\sqrt{y} + \sqrt{z} + \sqrt{x}} + \frac{\sqrt{z}}{\sqrt{z} + \sqrt{x} + \sqrt{y}} = \frac{\sqrt{x} + \sqrt{y} + \sqrt{z}}{\sqrt{x} + \sqrt{y} + \sqrt{z}} = 1$

Vậy P_max = 1 khi $x = y = z = \frac{1}{3}$ .

Câu 45: Cho tam giác ABC có P là trung điểm của AB và hai điểm M, N thỏa các hệ thức: $\vec{M B} - 2 \vec{M C} = \vec{0}$ và $\vec{N A} + 2 \vec{N C} = \vec{0}$ . Chứng minh rằng 3 điểm M, N, P thẳng hàng.

Lời giải:

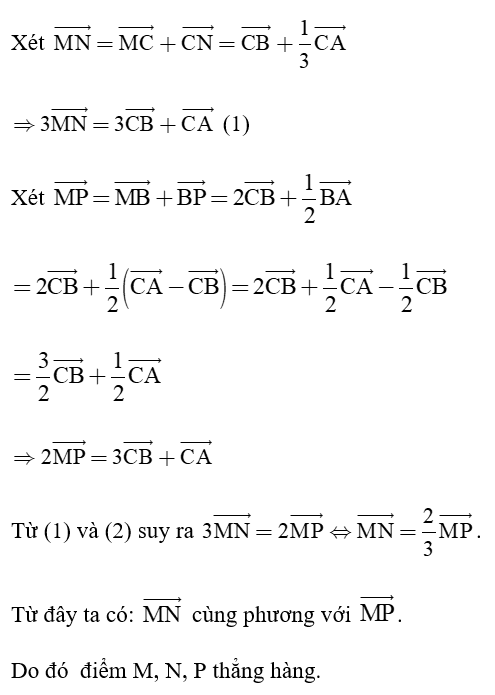
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 17)

Câu 46: Phân tích đa thức thành nhân tử: (ab – 1)² + (a + b)².

Lời giải:

(ab – 1)² + (a + b)²

= a²b² – 2ab + 1 + a² + 2ab + b²

= a²b² + a² + b² + 1

= a²(b² + 1) + (b² + 1)

= (b² + 1)(a² + 1).

Câu 47: Tính A = 1.2 + 2.3 + 3.4 +…+ n(n + 1).

Lời giải:

Ta thấy mỗi số hạng của tổng trên là tích của hai số tự nhiên liên tiếp, khi đó ta có:

Gọi a₁ = 1. 2 ⇒ 3.a₁ = 1. 2. 3 ⇒ 3.a₁ = 1. 2. 3 – 0. 1. 2

a₂ = 2. 3 ⇒ 3.a₂ = 2. 3. 3 ⇒ 3.a₂ = 2. 3. 4 – 1. 2. 3

a₃ = 3. 4 ⇒ 3.a₃ = 3. 3. 4 ⇒ 3.a₃ = 3. 4. 5 – 2. 3. 4

…

a_{n – 1} = (n – 1)n ⇒ 3. a_{n – 1} = 3(n – 1)n ⇒ 3.a_{n – 1} = (n – 1)n(n + 1) – (n – 2)(n – 1)n

a_n = n(n + 1) ⇒ 3a_n = 3n(n + 1) ⇒ 3a_n = n(n + 1)(n + 2) – (n – 1)n(n + 1)

Cộng từng vế của các hằng đẳng thức, ta có:

3(a₁ + a₂ + … + a_n) = n(n + 1)(n + 2)

⇔ 3A= n(n + 1)(n + 2) ⇒ $A = \frac{n (n + 1) (n + 2)}{3}$ .

Vậy $A = \frac{n (n + 1) (n + 2)}{3}$ .

Câu 48: Khổ giấy A1 lớn gấp bao nhiêu lần khổ giấy A3?

A. 4 lần;

B. 8 lần;

C. 6 lần;

D. 16 lần.

Lời giải:

Đáp án đúng là: A

Khổ giấy A1 lớn hơn 4 lần khổ giấy A3.

Câu 49: Cho hai hàm số y = x² và y = mx + 4, với m là tham số. Khi m = 3, tìm tọa độ các giao điểm A, B của hai đồ thị của hai hàm số trên.

Lời giải:

Ta có phương trình hoành độ giao điểm: x²= mx + 4

⇔ x² – mx – 4 = 0.

Với m = 3 ta có: x² – 3m – 4 = 0.

Ta thấy 1 – (−3) – 4 = 0 nên ta có nghiệm của phương trình trên có hai nghiệm là:

x₁ = −1 và x₂ = 4.

Với x₁ = −1 suy ra y₁ = 1 A( −1; 1).

Với x₂ = 4 suy ra y₂ = 16 B(4; 16).

Vậy với m = 3 ta có tọa độ của hai giao điểm là: A( −1; 1); B(4; 16).

Câu 50: Cho hai tập hợp khác rỗng A = (m – 1; 4]; B = (−2; 2m + 2), m ∈ ℝ. Tìm m để A ∩ B ≠ Ø.

A. −2 < m < 5;

B. m > −3;

C. −1< m < 5;

D. 1 < m < 5.

Lời giải:

Đáp án đúng là: A

Do $A \neq \emptyset; B \neq \emptyset$ ta có điều kiện:

$\{\begin{cases} m - 1 < 4 \\ 2 m + 2 > - 2 \end{cases} \Leftrightarrow \{\begin{cases} m < 5 \\ m > - 2 \end{cases}$ ⇔ −2< m < 5 (*)

Để A ∩ B = Ø ⇔ 2m + 2 ≤ m – 1 ⇔ m ≤ −3 (không thuộc khoảng (*)).

Do đó không có giá trị nào của m để A ∩ B = Ø.

Vậy với mọi m ∈ (−2; 5) thì A ∩ B ≠ Ø.

Vậy A đúng.

Câu 51: Tìm tất cả số tự nhiên x, y sao cho 2^x + 5^y là số chính phương.

Lời giải:

Đặt 2^x + 5^y = k², k ∈ ℕ (1)

Với y = 0 ta có: 2^x + 1 = k² $\Rightarrow$ (k – 1)(k + 1) = 2^x (2)

Dễ thấy x = 0 không phải là nghiệm của (1)

Với x > 0 thì k² = 2^x + 1 > 1 $\Rightarrow$ k > 1.

Câu 52: Một bó hoa 12 bông gồm: 5 hoa hồng, 4 hoa lan còn lại là hoa cúc. Chọn ngẫu nhiên 5 bông hoa. Tính xác suất sao cho chọn đủ ba loại và số cúc không ít hơn 2.

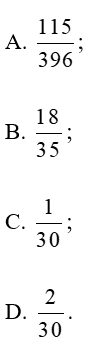
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 18)

Lời giải:

Đáp án đúng là: A

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 19)

Câu 53: Trong khai triển (x – 2)¹⁰⁰ = a₀ + a₁x¹ + … + a₁₀₀x¹⁰⁰. Tổng hệ số

a₀ + a₁ + a₂ + … + a₁₀₀ bằng:

A. −1;

B. 1;

C. 3¹⁰⁰;

D. 2¹⁰⁰.

Lời giải:
Đáp án đúng là: B

Ta có: a₀ + a₁x¹ + … + a₁₀₀x¹⁰⁰ = (x – 2)¹⁰⁰ (*)

Với x = 1 thì khi đó (*) trở thành:

a₀ + a₁ + a₂ + … + a₁₀₀ = (1 – 2)¹⁰⁰ = 1¹⁰⁰ = 1.

Câu 54: Tính tổng min và max của hàm số: $y = \sqrt{2 + x} + \sqrt{2 - x} + 2 \sqrt{4 - x^{2}}$ .

Lời giải:
ĐKXĐ: −2 ≤ x ≤ 2.

Đặt $\sqrt{x + 2} = a; \sqrt{2 - x} = b$ (a, b ≥ 0).

$\Rightarrow$ a² + b² = 4.

Ta có: y = a + b + 2ab.

• Tìm min:

$y = \sqrt{{(a + b)}^{2}} + 2 a b = \sqrt{a^{2} + b^{2} + 2 a b} + 2 a b = \sqrt{4 + 2 a b} + a b$ .

Vì a, b ∈ [0; 2] ⇒ ab ≥ 0.

$\Rightarrow y \geq \sqrt{4 + 0} + 0 \Leftrightarrow y \geq 2$ .

Vậy y_min = 2 ⇔ ab = 0 ⇔ x = ± 2.

• Tìm max:

Áp dụng bất đẳng thức Cô-si, ta có:

$a b \leq \frac{{(a + b)}^{2}}{4} \Rightarrow y \leq a + b + \frac{{(a + b)}^{2}}{2}$ (1)

Tiếp tục áp dụng bất đẳng thức Cô-si:

a² + b² ≥ 2ab ⇔ 2(a² + b²) ≥ (a + b)²

⇔ (a + b)² ≤ 8 $\Rightarrow a + b \leq 2 \sqrt{2}$ (2)

Từ (1) và (2)

Do đó y_max $= 4 + 2 \sqrt{2}$ .

Dấu “=” xảy ra khi a = b $\Leftrightarrow \sqrt{2 + x} = \sqrt{2 - x} \Leftrightarrow x = 0$ .

Vậy y_max + y_min = $2 + 4 + 2 \sqrt{2} = 6 + 2 \sqrt{2}$ .

Câu 55: Hình lăng trụ có thể có số cạnh nào sau đây?

A. 2015;

B. 2017;

C. 2018;

D. 2016.

Lời giải:

Đáp án đúng là: D

Nếu hình lăng trụ có đáy là đa giác n cạnh thì số cạnh đáy của hình lăng trụ là 2n và số cạnh bên là n.

Do đó tổng số cạnh của hình lăng trụ là 3n.

Vậy số cạnh của hình lăng trụ là một số chia hết cho 3.

Suy ra loại các đáp án A, B, C.

Đáp án D đúng vì 2016 chia hết cho 3.

Câu 56: Phân tích đa thức thành nhân tử x² + 5x – 6.

Lời giải:

x² + 5x – 6 = x² + 6x – x – 6

= x(x + 6) – (x + 6)

= (x + 6)(x – 1).

Câu 57: Công thức tính diện tích tam giác đều cạnh a.

Lời giải:

Công thức tính diện tích tam giác đều cạnh a là: $S = a^{2} \frac{\sqrt{3}}{4}$ .

Trong đó: S là diện tích tam giác đều; a là độ dài cạnh của tam giác.

Câu 58: Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:

− ∞ 1 2 3 4 + ∞

f’(x)

- 0 + 0 - 0 - 0 +

Hàm số y = 3f(x + 2) – x³ + 3x đồng biến trên khoảng nào dưới đây?

A. (1; +∞);

B. (−∞; 1);

C. (−1; 0);

D. (0; 2).

Lời giải:

Ta có: y = 3f(x + 2) – x³ + 3x

⇒ y' = 3f '(x + 2) – 3x² + 3.

Xét −1 < x < 0 ta có: $\{\begin{cases} 1 < x + 2 < 2 \Rightarrow f' (x + 2) > 0 \\ x^{2} < 1 \Rightarrow x^{2} - 1 < 0 \end{cases}$

⇒ 3f '(x + 2) – 3x² + 3 > 0 $\forall x \in (0; 1)$ .

Vậy hàm số đã cho đồng biến trên (−1; 0).

Câu 59: Cho đồ thị hàm số y = f(x) có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình $f (x) = \frac{1}{2}$ là:

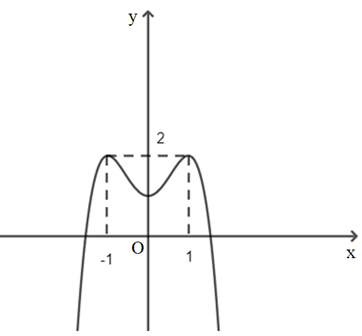
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 20)

A. 2;

B. 4;

C. 1;

D. 3.

Lời giải:

Đáp án đúng là: A

Số nghiệm thực của phương trình $f (x) = \frac{1}{2}$ chính là số giao điểm của đồ thị hàm số f(x) với đường thẳng $y = \frac{1}{2}$ .

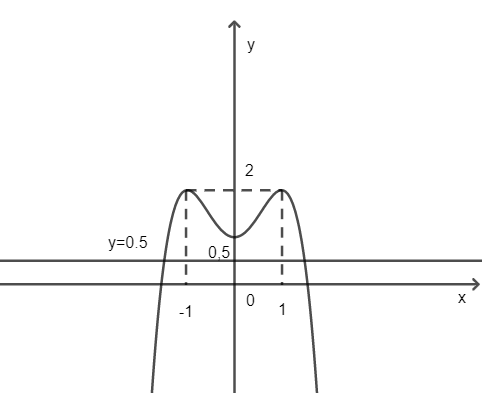
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) (ảnh 21)

Dựa vào hình trên ta thấy đồ thị hàm số f(x) với đường thẳng $y = \frac{1}{2}$ có hai giao điểm.

Vậy phương trình f(x) = $\frac{1}{2}$ có hai nghiệm.

Câu 60: Tìm số nguyên tố p để p + 2 và p + 10 cũng là số nguyên tố.

Lời giải:
TH1: p = 2.

Khi đó p + 2 = 4 là hợp số (loại).

TH2: p = 3

Khi đó p + 2 = 5; p + 3 = 13 đều là những số nguyên tố. ( thỏa mãn).

TH3: p > 3.

Khi đó p = 3k + 1 hoặc p = 3k + 2 (k ∈ ℕ*)

• p = 3k + 1 $\Rightarrow$ p + 2 = 3k + 3 = 3(k + 3) luôn có một ước là 3.

Do đó p = 3k + 1 là hợp số (loại).

• p = 3k + 2 $\Rightarrow$ p + 10 = 3k + 2 + 10 = 3k + 12 = 3(k + 4) luôn có một ước là 3.

Do đó p = 3k + 2 là hợp số (loại).

Vậy ta có 1 số nguyên tố p = 3 thỏa mãn duy nhất.

Từ khóa :

Giải bài tập

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

295

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

315

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

343

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

290

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23)

Lời giải:

Đáp án đúng là: A

Câu 19: Cho $Δ A B C$ vuông tại A điểm M thuộc cạnh BC từ M vẽ các đường thẳng vuông góc với AB ở D vuông góc với AC ở E

a) cm AM = BE.

b) gọi l là điểm đx của D qua A và K là điểm đx của E qua M cm IK, DE, AM đồng quy hai trung điểm O của mỗi đoạn.

c) gọi AH là đường cao của tính số đo $\hat{D H E}$ .

Từ khóa :

Đánh giá

Bài viết cùng môn học

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23)

Lời giải:

Đáp án đúng là: A

a) cm AM = BE.

b) gọi l là điểm đx của D qua A và K là điểm đx của E qua M cm IK, DE, AM đồng quy hai trung điểm O của mỗi đoạn.

c) gọi AH là đường cao của tính số đo DHE^ .

Từ khóa :

Đánh giá

Bài viết cùng môn học

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

c) gọi AH là đường cao của tính số đo $\hat{D H E}$ .