Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD với O
Câu 14: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD với O là giao điểm hai đường chéo AC và BD. Gọi M,N lần lượt là trung điểm các cạnh SA và SD. 1. Chứng minh MO song song với mặt phẳng (SBC) và mặt phẳng (OMN) song song với mặt phẳng (SBC).
2. Gọi K là trung điểm của MO. Chứng minh NK song song với (SBC).
3. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (OMN). Hỏi thiết diện là hình gì ?
Lời giải:
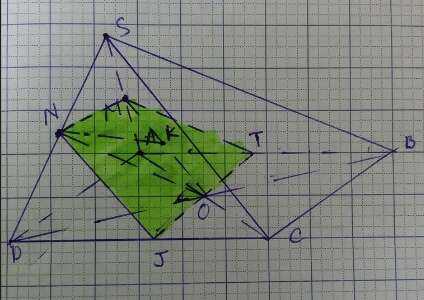
1) Ta có: MO là đường trung bình ΔSAC nên MO//SC mà SC⊂(SBC)
Vậy MO//(SBC)
Ta có:
MO//SC
NO//SB
MO, NO⊂(OMN); SC, SB⊂(SBC)
Vậy (OMN)//(SBC)
2) Ta có: (OMN)//(SBC)
Mà NK ⊂ (OMN)
Nên NK//(SBC)
3) Xét (OMN) và (ABCD):
Ta Có:
+) O là điểm chung 1
+) NM//AD (đường TB của tam giác)
Qua O vẽ đường thẳng song song với AD cắt AB tại T, cắt CD tại J
Vậy JT =(OMN) ∩ (ABCD) (1)
(OMN) ∩ (SAD)=MN (2)
(OMN) ∩ (SCD)=NJ (3)
(OMN) ∩ (SAB)=MT (4)
Từ 4 điều trên vậy thiết diện hình thang NMTJ (vì NM//TJ//AD).
Xem thêm các bài giải Tổng hợp kiến thức môn Toán hay, chi tiết khác:
Câu 2: Tính bằng cách thuận tiện nhất: 34 000 : 125 : 8
Câu 4: Phân tích thành nhân tử 5(x + 3y) - 15x ( x + 3y )
Câu 6: Cho có A(5; 3); B(2; -1) và C(-1; 5). Tính tọa độ chân đường cao vẽ từ A.
Câu 8: Cho ABC có AB = 6cm, AC = 3cm, M là điểm thỏa mãn. Tính độ dài đoạn AM.
Câu 10: Số lớn nhất có 4 chữ số khác nhau và tích các chữ số bằng 24 là ………
Câu 12: Chứng minh biểu thức sau
Câu 14: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD với O là giao điểm hai đường chéo AC và BD. Gọi M,N lần lượt là trung điểm các cạnh SA và SD. 1. Chứng minh MO song song với mặt phẳng (SBC) và mặt phẳng (OMN) song song với mặt phẳng (SBC).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.