Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 84) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 84)
Câu 1: Viết số đo đại lượng dưới dạng số thập phân: 9 dm 2 cm 7 mm = ... dm.
Lời giải:
Ta có 9 dm 2 cm 7 mm = 9,27 dm.
Câu 2: Một lớp học có 50 học sinh được đăng kí chơi 2 môn thể thao: cầu lông và bóng bàn. Có 30 bạn đăng kí chơi cầu lông, 28 bạn chơi bóng bàn và 10 bạn không chơi môn nào. Hỏi có bao nhiêu bạn đăng kí chơi cả 2 môn và bao nhiêu bạn đăng kí chơi 1 môn?
Lời giải:
Gọi X là tập hợp các học sinh trong lớp.
Gọi A, B lần lượt là tập hợp các học sinh đăng kí chơi cầu lông và chơi bóng bàn.
Suy ra n(A) = 30, n(B) = 28.
Như vậy tập hợp học sinh đăng kí chơi cả 2 môn và tập hợp học sinh đăng kí chơi ít nhất 1 môn lần lượt là A ∩ B và A ∪ B.
Ta có n(A ∪ B) = 50 – 10 = 40.
Lại có n(A ∪ B) = n(A) + n(B) – n(A ∩ B).
Suy ra n(A ∩ B) = n(A) + n(B) – n(A ∪ B) = 30 + 28 – 40 = 18.
Số học sinh chỉ đăng kí chơi 1 môn là: n(A ∪ B) – n(A ∩ B) = 40 – 18 = 22.
Vậy có 18 học sinh đăng kí chơi cả 2 môn và có 22 học sinh chỉ đăng kí chơi 1 môn.
Câu 3: Một mảnh ruộng hình chữ nhật được chia làm 2 phần để trồng hành và trồng cà rốt. Trong đó diện tích trồng cà rốt gấp 5 lần diện tích trồng hành. Chu vi phần đất trồng cà rốt lớn hơn chu vi phần đất trồng hành 936 m. Biết chiều rộng ban đầu là 327 m. Hỏi chu vi mảnh ruộng ban đầu là bao nhiêu đề-ca-mét?
Lời giải:
Vì diện tích trồng cà rốt gấp 5 lần diện tích trồng hành nên cạnh còn lại của diện tích trồng cà rốt gấp 5 lần cạnh còn lại của phần trồng hành.
Cạnh còn lại của diện tích trồng hành là:
936 : 2 : (5 – 1) × 1 = 117 (m)
Cạnh còn lại của diện tích trồng cà rốt là:
117 × 5 = 585 (m)
Chiều dài của mảnh đất ban đầu là:
117 + 585 = 702 (m)
Chu vi mảnh ruộng ban đầu là:
(702 + 327) × 2 = 2058 (m) = 205,8 (dam)
Vậy chu vi mảnh ruộng ban đầu là 205,8 dam.
Câu 4: Một tuần lễ cửa hàng bán được 314,78 m vải, tuần lễ sau bán được 525,22 m vải. Biết rằng của hàng đó bán tất cả các ngày trong tuần hỏi trung bình mỗi ngày cửa hàng đó bán được bao nhiêu mét vải?
Lời giải:
Số mét vải cửa hàng bán được trong hai tuần là:
314,78 + 525,22 = 840 (m)
Số ngày trong hai tuần là:
7 × 2 = 14 (ngày)
Trung bình mỗi ngày bán được số mét vải là:
840 : 14 = 60 (m)
Đáp số : 60 m vải.
Câu 5: Rút gọn biểu thức (2x + 3y)2 + (3x – 2y)2 – 2(2x + 3y)(3x – 2y).
Lời giải:
Ta có (2x + 3y)2 + (3x – 2y)2 – 2(2x + 3y)(3x – 2y).
= (2x + 3y)2 – 2(2x + 3y)(3x – 2y) + (3x – 2y)2.
= (2x + 3y – 3x + 2y)2.
= (5y – x)2.
Câu 6: Tìm dấu hiệu chia hết cho 11.
Lời giải:
Dấu hiệu chia hết cho 11: Tổng các chữ số hàng lẻ – Tổng các chữ số hàng chẵn hoặc ngược lại chia hết cho 11 thì số đó chia hết cho 11.
Câu 7: Số học sinh khối 6 của trường khi xếp thành 12 hàng, 15 hàng hay 18 hàng đều dư ra 9 học sinh. Hỏi số học sinh khối 6 trường đó là bao nhiêu? Biết rằng số đó lớn hơn 300 và nhỏ hơn 400.
Lời giải:
Do số học sinh khối 6 của trường khi xếp thành 12 hàng, 15 hàng hay 18 hàng đều dư ra 9 học sinh nên số học sinh khối 6 của trường đó khi chia cho 12, 15, 18 đều dư 9.
Vì vậy nếu ta bỏ bớt 9 học sinh thì khi xếp hàng 12, 15, 18 đều vừa đủ.
Khi đó số học sinh khối 6 của trường đó là bội chung của 12, 15, 18.
Suy ra số học sinh khối 6 của trường đó là bội của BCNN(12, 15, 18).
Ta có 12 = 22.3; 15 = 3.5; 18 = 2.32.
Suy ra BCNN(12, 15, 18) = 22.32.5 = 180.
Do đó số học sinh khối 6 của trường đó là 180k + 9, với k ∈ ℕ*.
Lại có số học sinh khối 6 của trường đó lớn hơn 300 và nhỏ hơn 400.
Tức là, 300 < 180k + 9 < 400.
⇔ 291 < 180k < 391.
.
Mà k ∈ ℕ* nên k = 2.
Vậy số học sinh khối 6 của trường đó là 180.2 + 9 = 369 (học sinh).
Câu 8: Tìm x, biết x% : 3 + 45% = 0,7.
Lời giải:
x% : 3 + 45% = 0,7.
x% : 3 + 0,45 = 0,7.
x% : 3 = 0,7 – 0,45 = 0,25.
x% = 0,25 . 3 = 0,75.
x% = 75%.
x = 75.
Vậy x = 75.
Câu 9: Tính: 2083,25 – (37 – 25,4) : 0,8 + 3,5 × 2,5.
Lời giải:
Ta có 2083,25 – (37 – 25,4) : 0,8 + 3,5 × 2,5
= 2083,25 – 11,6 : 0,8 + 8,75
= 2083,25 – 14,5 + 8,75
= 2068,75 + 8,75
= 2077,5.
Câu 10: Bạn An mỗi ngày giải ít nhất một bài toán, nhưng mỗi tuần giải không quá 13 bài toán. Chứng minh có một số ngày liên tiếp mà bạn ấy giải đúng 20 bài toán.
Lời giải:
Gọi n1 là số bài toán bạn An đã giải trong ngày đầu tiên;
n2 là số bài toán bạn An đã giải trong hai ngày đầu;
n3 là số bài toán bạn An đã giải trong ba ngày đầu;
n4 là số bài toán bạn An đã giải trong bốn ngày đầu;
...
n77 là số bài toán bạn An đã giải trong 77 ngày đầu (11 tuần).
Theo đề, ta có mỗi tuần bạn An giải không quá 13 bài toán.
Tức là, n77 ≤ 11.13 = 143.
Ta xét tập hợp các số tự nhiên M = {n1; n2; n3; ...; n77; n1 + 20; n2 + 20; ...; n77 + 20}.
Tập hợp M chứa 154 phần tử và phần tử lớn nhất là n77 + 20 ≤ 143 + 20 = 163.
Theo nguyên lí Dirichlet, trong M có ít nhất hai số bằng nhau.
Mà các số n1, n2, n3, ..., n77 là hoàn toàn khác nhau.
Suy ra tồn tại hai số nh và nk sao cho nh = nk + 20, với 1 < h ≤ 77.
Do đó nh – nk = 20.
Điều này có nghĩa là ngày thứ k + 1 đến ngày thứ h, bạn An phải giải đúng 20 bài toán.
Vậy ta có điều phải chứng minh.
Câu 11: Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh AH < BC.
Lời giải:
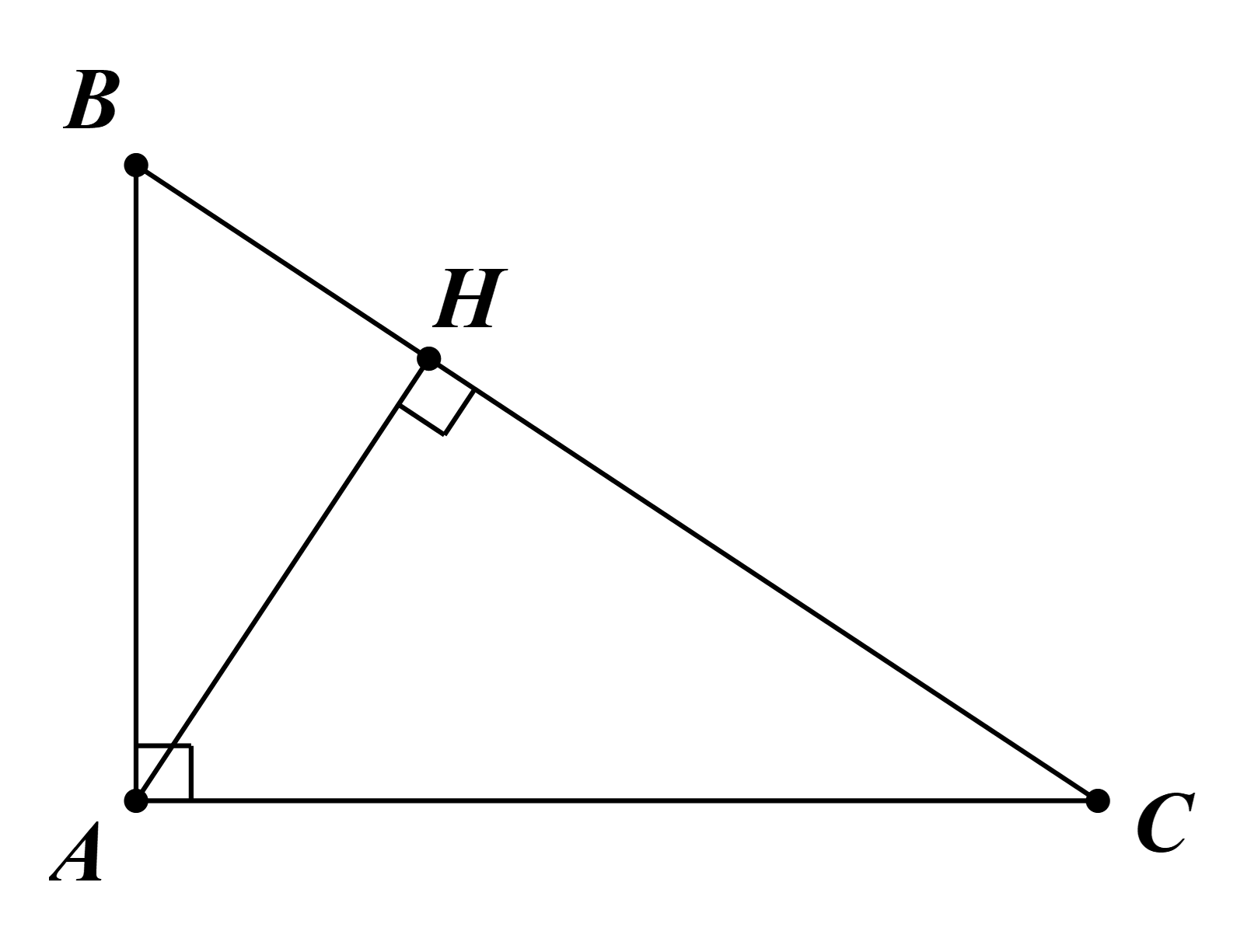
Tam giác AHC vuông tại H có AC là cạnh huyền.
Suy ra AC là cạnh lớn nhất.
Do đó AH < AC (1)
Tam giác ABC vuông tại A có BC là cạnh huyền.
Suy ra BC là cạnh lớn nhất.
Do đó AC < BC (2)
Từ (1), (2), ta thu được AH < AC < BC.
Vậy AH < BC.
Câu 12: Một khu đất hình chữ nhật có chiều dài là 42 m; chiều rộng kém chiều dài 16 m. Biết rằng nếu tăng chiều rộng và giảm chiều dài thì khu đất đó trở thành hình vuông. Tính diện tích khu đất hình vuông đó.
Lời giải:
Chiều rộng khu đất hình chữ nhật là: 42 – 16 = 26 (m).
Phải tăng chiều rộng và giảm chiều dài số mét để khu đất đó trở thành hình vuông là: (42 – 26) : 2 = 8 (m).
Cạnh của khu đất hình vuông là: 26 + 8 = 34 (m).
Diện tích khu đất hình vuông đó là: 34 × 34 = 1156 (m2).
Đáp số: 1156 m2.
Câu 13: Một đội công nhân trồng rừng trung bình cứ 2 ngày trồng được 300 cây thông. Hỏi trong 5 ngày đội đó trồng được bao nhiêu cây thông?
Lời giải:
Số cây thông đội đó trồng được trong 1 ngày là: 300 : 2 = 150 (cây thông).
Số cây thông trong 5 ngày đội đó trồng được là: 150 × 5 = 750 (cây thông).
Đáp số: 750 cây thông.
Câu 14: Người thợ may lấy ra một tấm vải dài để cắt may 4 bộ quần áo, mỗi áo hết 300 cm và mỗi quần hết 325 cm. Sau khi cắt xong thì tấm vải còn lại dài 2 m. Hỏi tấm vải ban đầu dài bao nhiêu cm?
Lời giải:
Đổi 2 m = 200 cm.
Một bộ quần áo (1 áo + 1 quần) hết số vải là:
300 + 325 = 625 (cm).
Bốn bộ quần áo hết số vải là:
625 × 4 = 2500 (cm).
Tấm vải ban đầu dài là:
2500 + 200 = 2700 (cm).
Đáp số: 2700 cm.
Câu 15: Một trong các bạn A, B, C và D làm vỡ kính cửa sổ. Khi được hỏi, họ trả lời như sau:
A: “C làm vỡ”.
B: “Không phải tôi”.
C: “D làm vỡ”.
D: “C đã nói dối”.
Nếu có đúng một người nói thật thì ai đã làm vỡ cửa sổ.
A. A làm vỡ kính cửa sổ;
B. B làm vỡ kính cửa sổ;
C. C làm vỡ kính cửa sổ;
D. D làm vỡ kính cửa sổ.
Lời giải:
Trường hợp 1: A, B nói thật ⇒ D nói dối ⇒ C nói thật.
⇒ Loại.
Trường hợp 2:
⦁ C nói thật ⇒ D làm vỡ.
⦁ C nói thật ⇒ B nói dối ⇒ B làm vỡ (mâu thuẫn).
⇒ Loại.
Trường hợp 3: D nói thật ⇒ B nói dối ⇒ B làm vỡ (nhận).
Vậy ta chọn phương án B.
Câu 16: Trong phép chia có số bị chia là 72, số chia là số kém số bé nhất có hai chữ số 2 đơn vị. Tính thương của hai số đó.
Lời giải:
Số bé nhất có hai chữ số là: 10.
Số chia là: 10 – 2 = 8.
Thương của hai số đó là: 72 : 8 = 9.
Đáp số: 9.
Câu 17: Chứng minh rằng a3 + b3 + c3 ≥ 3abc, với a, b, c > 0.
Lời giải:
Ta có a > 0. Suy ra a3 > 0.
Chứng minh tương tự, ta được b3 > 0, c3 > 0.
Áp dụng bất đẳng thức Cauchy cho ba số a3, b3, c3, ta được: a3 + b3 + c3 ≥ 3abc.
Vậy ta có điều phải chứng minh.
Câu 18: Cho a + b + c = 0 và a2 + b2 + c2 = 2. Tính giá trị biểu thức a4 + b4 + c4.
Lời giải:
Ta có a + b + c = 0.
⇔ (a + b + c)2 = 0.
⇔ a2 + b2 + c2 + 2(ab + bc + ca) = 0.
⇔ 2 + 2(ab + bc + ca) = 0.
⇔ 2(ab + bc + ca) = –2.
⇔ ab + bc + ca = –1.
Ta có ab + bc + ca = –1.
Suy ra (ab + bc + ca)2 = 1.
⇔ a2b2 + b2c2 + c2a2 + 2(ab2c + bc2a + a2bc) = 1.
⇔ a2b2 + b2c2 + c2a2 + 2abc(b + c + a) = 1.
⇔ a2b2 + b2c2 + c2a2 + 2abc.0 = 1.
⇔ a2b2 + b2c2 + c2a2 = 1.
Đặt P = a4 + b4 + c4
= (a2 + b2 + c2)2 – 2(a2b2 + b2c2 + c2a2)
= 22 – 2.1 = 2.
Vậy a4 + b4 + c4 = 2.
Câu 19: Để chuyên chở 39 kg hàng hóa trên quãng đường dài 74 km phải chi phí hết 120 000 đồng. Hỏi phải chi phí hết bao nhiêu tiền nếu phải chuyên chở 26 kg hàng hóa trên quãng đường dài 185 km?
Lời giải:
Chi phí chở 26 kg trên quãng đường dài 74 km là:
120 000 : 39 × 26 = 80 000 (đồng).
Chi phí chở 26 kg trên quãng đường dài 185 km là:
80 000 : 74 × 185 = 200 000 (đồng).
Đáp số: 200 000 đồng.
Câu 20: Một vườn trẻ dự trữ gạo cho 120 em bé ăn trong 20 ngày. Sau đó có thêm một số em bé mới đến nên số ngày ăn giảm đi 4 ngày. Hỏi có bao nhiêu em bé mới đến thêm?
Lời giải:
Để ăn hết số gạo đó trong 1 ngày cần số em là:
120 × 20 = 2400 (em)
Số gạo còn ăn được trong số ngày nữa là:
20 – 4 = 16 (ngày)
Số em đến thêm là:
(2400 : 16) – 120 = 30 (em)
Đáp số: 30 em.
Câu 21: Một đội công nhân có 38 người nhận sửa một đoạn đường dài 1330 m trong 5 ngày. Hỏi muốn sửa đoạn đường tương tự dài 1470 m trong 2 ngày thì cần bao nhiêu công nhân? (mức làm của mỗi người đều như nhau).
Lời giải:
Trong một ngày 38 người sửa được đoạn đường là:
1330 : 5 = 266 (m).
Một người trong một ngày sửa được đoạn đường là:
266 : 38 = 7 (m).
Một người trong hai ngày sửa được đoạn đường là:
7 × 2 = 14 (m).
Sửa đoạn đường dài 1470 m trong 2 ngày thì cần số công nhân là:
1470 : 14 = 105 (công nhân).
Đáp số: 105 công nhân.
Câu 22: Một đơn vị bộ đội chuẩn bị đủ gạo cho 750 người ăn trong 40 ngày nhưng vì có một số người đến thêm nên anh quản lí tính ra số gạo đó chỉ đủ ăn trong 25 ngày. Hỏi số người đến thêm là bao nhiêu người? (Biết suất ăn của mỗi người là như nhau).
Lời giải:
Coi 1 người ăn 1 ngày là 1 suất.
Tổng số suất gạo là: 750 × 40 = 30 000 (suất).
Số người ăn trong 25 ngày là: 30 000 : 25 = 1200 (người).
Số người đến thêm là: 1200 – 750 = 450 (người).
Đáp số: 450 người.
Câu 23: Một bếp ăn dự trữ gạo đủ cho 120 người ăn trong 18 ngày. Nay có 80 người được chuyển đi nơi khác. Hỏi số gạo đó đủ cho những người còn lại ăn trong bao nhiêu ngày? (Mức ăn của mỗi người như nhau).
Lời giải:
Số người còn lại là:
120 – 80 = 40 (người)
120 người gấp 40 người số lần là:
120 : 40 = 3 (lần)
Số gạo đó đủ cho số người còn lại ăn trong thời gian là:
18 × 3 = 54 (ngày)
Đáp số: 54 ngày.
Câu 24: Phân tích các số sau ra thừa số nguyên tố: 96; 90; 42.
Lời giải:
Ta có: 96 = 25.3; 90 = 2.32.5 và 42 = 2.3.7.
Câu 25: Gọi x là số tự nhiên thỏa mãn 3x – 1 – 25 = 56. Chọn câu đúng:
A. x < 6.
B. x > 7.
C. x < 5.
D. x < 4.
Lời giải:
Đáp án đúng là: A
3x – 1 – 25 = 56
3x – 1 = 56 + 25
3x – 1 = 81
3x – 1 = 34
x – 1 = 4
x = 4 + 1
x = 5.
Ta thấy x = 5 < 6.
Vậy ta chọn phương án A.
Câu 26: Tìm x, biết:
a) 5.22 + (x + 3) = 52.
b) 23 + (x – 32) = 53 – 43.
c) 4.(x – 5) – 23 = 24.3.
d) 5.(x + 7) – 10 = 23.5.
Lời giải:
a) 5.22 + (x + 3) = 52.
⇒ 5.4 + (x + 3) = 25.
⇒ 20 + (x + 3) = 25.
⇒ x + 3 = 25 – 20.
⇒ x + 3 = 5.
⇒ x = 5 – 3.
⇒ x = 2.
Vậy x = 2.
b) 23 + (x – 32) = 53 – 43.
⇒ 8 + (x – 9) = 125 – 64.
⇒ 8 + (x – 9) = 61.
⇒ x – 9 = 61 – 8.
⇒ x – 9 = 53.
⇒ x = 53 + 9.
⇒ x = 62.
Vậy x = 62.
c) 4.(x – 5) – 23 = 24.3.
⇒ 4.(x – 5) – 8 = 16.3.
⇒ 4.(x – 5) – 8 = 48.
⇒ 4.(x – 5) = 48 + 8.
⇒ 4.(x – 5) = 56.
⇒ x – 5 = 56 : 4.
⇒ x – 5 = 14.
⇒ x = 14 + 5.
⇒ x = 19.
Vậy x = 19.
d) 5.(x + 7) – 10 = 23.5.
⇒ 5.(x + 7) – 10 = 8.5.
⇒ 5.(x + 7) – 10 = 40.
⇒ 5.(x + 7) = 40 + 10.
⇒ 5.(x + 7) = 50.
⇒ x + 7 = 50 : 5.
⇒ x + 7 = 10.
⇒ x = 10 – 7.
⇒ x = 3.
Câu 27: Thực hiện phép tính:
a) 5 . 22 – 18 : 32.
b) 17 . 85 + 15 . 17 – 120.
c) 23 . 17 – 23 . 14.
d) 20 – [30 – (5 – 1)2].
Lời giải:
a) 5 . 22 – 18 : 32
= 5 . 4 – 18 : 9
= 20 – 2
= 18.
b) 17 . 85 + 15 . 17 – 120
= 17 . (85 + 15) – 120
= 17 . 100 – 120
= 1700 – 120
= 1580.
c) 23 . 17 – 23 . 14
= 23 . (17 – 14)
= 8 . 3
= 24.
d) 20 – [30 – (5 – 1)2]
= 20 – (30 – 42)
= 20 – (30 – 16)
= 20 – 14
= 6.
Câu 28: Hiện nay, anh 13 tuổi và em 3 tuổi. Hỏi sau bao nhiêu năm nữa thì tuổi anh sẽ gấp 3 lần tuổi em?
Lời giải:
Anh luôn hơn em số tuổi là: 13 – 3 = 10 (tuổi).
Khi tuổi anh gấp 3 lần tuổi em, ta có sơ đồ sau:
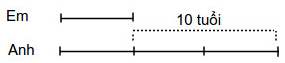
Hiệu số phần bằng nhau là: 3 – 1 = 2 (phần).
Tuổi của em lúc đó là: 10 : 2 = 5 (tuổi).
Số năm nữa thì tuổi anh sẽ gấp 3 lần tuổi em là: 5 – 3 = 2 (năm).
Đáp số: 2 năm.
Câu 29: Cho A = 3 + 32 + 33 + ... + 3100. Tìm số tự nhiên n biết rằng 2A + 3 = 3n.
A. n = 99.
B. n = 100.
C. n = 101.
D. n = 102.
Lời giải:
Ta có A = 3 + 32 + 33 + ... + 3100.
Suy ra 3A = 32 + 33 + 34 + ... + 3101.
Do đó 3A – A = (32 + 33 + 34 + ... + 3101) – (3 + 32 + 33 + ... + 3100).
Suy ra 2A = (32 – 32) + (33 – 33) + ... + (3100 – 3100) + 3101 – 3.
Vì vậy 2A = 3101 – 3.
Theo đề, ta có 2A + 3 = 3n.
⇒ 3101 – 3 + 3 = 3n.
⇒ 3101 = 3n.
⇒ n = 101 (nhận).
Vậy n = 101.
Do đó ta chọn phương án C.
Câu 30: Cho A = 3 + 32 + 33 + ... + 3100. Tìm x ∈ ℕ sao cho 2A + 3 = 3x + 100.
Lời giải:
Ta có A = 3 + 32 + 33 + ... + 3100.
Suy ra 3A = 32 + 33 + 34 + ... + 3101.
Do đó 3A – A = (32 + 33 + 34 + ... + 3101) – (3 + 32 + 33 + ... + 3100).
Suy ra 2A = (32 – 32) + (33 – 33) + ... + (3100 – 3100) + 3101 – 3.
Vì vậy 2A = 3101 – 3.
Theo đề, ta có 2A + 3 = 3x + 100.
⇒ 3101 – 3 + 3 = 3x + 100.
⇒ 3101 = 3x + 100.
⇒ x + 100 = 101.
⇒ x = 101 – 100 = 1 (nhận).
Vậy x = 1.
Câu 31: Học sinh khối 6 có 195 nam và 117 nữ tham gia lao động. Thầy phụ trách muốn chia ra thành các tổ sao cho số nam và nữ mỗi tổ đều bằng nhau. Hỏi có thể chia nhiều nhất thành mấy tổ? Mỗi tổ bao nhiêu nam, bao nhiêu nữ?
Lời giải:
Gọi số tổ là a (a ∈ ℕ*).
Khi đó ta có 195 ⋮ a và 117 ⋮ a và a lớn nhất.
Do đó a là ƯCLN(195, 117).
Ta có 195 = 3.5.13 và 117 = 32.13.
Suy ra ƯCLN(195, 117) = 3.13 = 39.
Do đó a = 39.
Vậy có thể chia nhiều nhất thành 39 tổ, mỗi tổ có 195 : 39 = 5 (nam) và 117 : 39 = 3 (nữ).
Câu 32: Một tàu hỏa cần chở 875 hành khách đi tham quan. Biết rằng mỗi toa có 10 ngăn, mỗi ngăn có 6 chỗ. Hỏi cần ít nhất mấy toa để chở hết số hành khách đó.
Lời giải:
Số chỗ ngồi của mỗi toa là: 6 . 10 = 60 (chỗ ngồi).
Ta có 875 : 60 = 14 dư 35.
Suy ra cần thêm 1 toa để chở 35 khách tham quan.
Cần ít nhất số toa để chở hết số khách tham quan là: 14 + 1 = 15 (toa).
Đáp số: 15 toa.
Câu 33: Cho dãy số: 3; 9; 15; 21; ...; 45; 51. Hãy tính trung bình cộng của các số trong dãy số đó./
Lời giải:
Khoảng cách giữa 2 số hạng liên tiếp trong dãy là: 6
Trung bình cộng của dãy số cách đều = (số đầu + số cuối) : 2
= (3 + 51) : 2 = 54 : 2 = 27
Vậy trung bình cộng của dãy số trên là 27.
Câu 34: Một khu nghỉ mát hình chữ nhật có chu vi 3 km 7 hm và chiều dài gấp 4 lần chiều rộng. Hỏi diện tích khu nghỉ mát đó là bao nhiêu mét vuông, bao nhiêu héc ta?
Lời giải:
Đổi: 3 km 7 hm = 3700 m
Nửa chu vi khu nghỉ mát là: 3700 : 2 = 1850 (m)
Tổng số phần bằng nhau là: 4 + 1 = 5 (phần)
Chiều rộng khu nghỉ mát là: 1850 : 5 × 1 = 370 (m)
Chiều dài khu nghỉ mát là: 370 × 4 = 1480 (m)
Diện tích khu nghỉ mát là: 1480 × 370 = 547 600 (m2)
Đổi: 547 600 m2 = 54,76 ha
Đáp số: 547 600 m2; 54,76 ha.
Câu 35: Nhà bếp dự trữ đủ lượng gạo cho 45 người ăn trong 6 ngày. Nếu có 54 người ăn số gạo đó thì số ngày ăn sẽ giảm đi bao nhiêu ngày (biết rằng suất ăn của mỗi người là như nhau).
Lời giải:
1 người ăn số gạo đó trong số ngày là: 45 × 6 = 270 (ngày)
54 người ăn thì số gạo đó ăn trong số ngày là: 270 : 54 = 5 (ngày)
Số ngày giảm đi khi có 54 người ăn là: 6 – 5 = 1 (ngày)
Đáp số: 1 ngày.
Câu 36: Ba học sinh, mỗi người mua một loại bút. Giá ba loại lần lượt là 1200 đồng, 1500 đồng, 2000 đồng. Biết số tiền phải trả là như nhau, hỏi mỗi học sinh mua ít nhất bao nhiêu chiếc bút?
Lời giải:
Gọi số tiền mỗi người ít phải trả là a (đồng; a ∈ )
Theo bài ra:
a chia hết cho 1200
a chia hết cho 1500
a chia hết cho 2000
⇒ a ∈ BC (1200, 1500, 2000)
Ta có:
1200 = 24.52.3;
1500 = 22.3.53;
2000 = 24.53.
⇒ BCNN (1200, 1500, 2000) = 24.53.3 = 6000
⇒ a = 6000 đồng
Số bút mua được với giá 1200 đồng là: 6000 : 1200 = 5 (bút);
Số bút mua được với giá 1500 đồng là: 6000 : 1500 = 4 (bút);
Số bút mua được với giá 2000 đồng là: 6000 : 2000 = 3 (bút).
Câu 37: Cho hình bình hành có chu vi là 900 cm, có độ dài cạnh đáy gấp 2 lần cạnh bên và gấp 4 lần chiều cao. Tính diện tích hình bình hành đó.
Lời giải:
Cách 1:
Nửa chu vi hình bình hành là: 900 : 2 = 450 (cm).
Tổng số phần bằng nhau của nửa chu vi là: 1 + 2 = 3 (phần)
Độ dài cạnh đáy hình bình hành là: 450 : 3 × 2 = 300 (cm).
Chiều cao hình bình hành là: 300 : 4 = 75 (cm).
Diện tích hình bình hành là: 300 × 75 = 22 500 (cm2).
Cách 2:
Gọi độ dài cạnh đáy là a, độ dài cạnh bên là b, chiều cao là h.
Do độ dài cạnh đáy gấp 2 lần cạnh bên nên a = 2b.
Ta có: a + b = 900 cm : 2 = 450 cm
⇔ 2b + b = 450 cm
⇔ 3b = 450 cm
⇔ b = 150 cm
⟹ a = 2b = 2 × 150 cm = 300 cm.
Mà theo giả thiết: a = 4h ⇒ h = a : 4 = 300cm : 4 = 75 cm
Diện tích hình bình hành: S = a × h = 300 cm × 75 cm = 22 500 cm2.
Vậy diện tích hình bình hành đó là 22 500 cm2.
Câu 38: Vụ mùa vừa qua, gia đình bác Tư thu hoạch từ hai thửa ruộng được 75 tạ thóc. Thửa ruộng thứ hai thu hoạch được nhiều hơn thửa ruộng thứ nhất 7 tạ thóc. Hỏi trên mỗi thửa ruộng bác Tư thu hoạch được bao nhiêu tạ thóc?
Lời giải:
Cách 1:
Thửa ruộng thứ nhất bác Tư thu hoạch được là: (75 – 7) : 2 = 34 (tạ thóc).
Thửa ruộng thứ hai bác Tư thu hoạch được là: 34 + 7 = 41 (tạ thóc).
Cách 2:
Gọi a và b lần lượt là số thóc thu hoạch được trên thửa ruộng thứ nhất và thứ hai (tạ), (a, b > 0).
Theo đề bài ta có: a + b = 75
⟺ a + (a + 7) = 75
⟺ 2a = 75 – 7
⟺ a = 68 : 2
⟺ a = 34
⇒ b = a + 7 = 34 + 7 = 41
Đáp số: Thửa ruộng thứ hai: 41 tạ; Thửa ruộng thứ nhất: 34 tạ.
Câu 39: Minh Quang trồng một số cây hoa trong vườn cây cảnh và thấy rằng số cây hoa của mình trồng được xếp thành 5 hàng và mỗi hàng có 4 cây mà số cây là ít nhất có thể. Vậy Minh Quang đã trồng … cây hoa.
Lời giải:
Minh Quang Đã trồng 9 cây (theo hình ngôi sao).
Câu 40: Một mảnh đất hình thang có diện tích 455m2, chiều cao là 13m. Tính độ dài mỗi đáy của mảnh đất hình thang đó, biết đáy bé kém đáy lớn 5m.
Lời giải:
Tổng độ dài hai đáy của hình thang là:
455 × 2 : 13 = 70 (m)
Độ dài đáy lớn của hình thang là:
(70 + 5) : 2 = 37,5 (m)
Độ dài đáy bé của hình thang là:
37,5 – 5 = 32,5 (m)
Đáp số: 37,5 m ; 32,5 m.
Câu 41: Một phép chia có số dư là số dư lớn nhất có thể có trong phép chia. Nếu gấp cả số bị chia và số chia lên 4 lần thì được phép chia mới có thương là 25 và số dư là 24. Tìm số bị chia và số chia.
Lời giải:
Gọi số bị chia là a; số chia là b
Ta có:
(a × 4) : (b × 4) = 25 (dư 24)
⇔ (a : b) × (4 : 4) = 25 (dư 24)
⇔ a : b = 25 (dư 24)
⇔ a = 25 × b + 24
Mà số dư là số lớn nhất có thể suy ra b sẽ là số bé nhất có thể và lớn hơn 24 nên b chỉ có thể bằng 25
⇒ a = 25 × 25 + 24 = 649
Vậy số bị chia là 649; số chia là 25.
Câu 42: Một đơn vị bộ đội dự kiến cần 45 người để hoàn thành 1 công việc trong 14 ngày sau đó để rút ngắn thời gian đơn vị đã điều động 70 người tham gia. Hỏi đơn vị đã hoàn thành trong bao nhiêu ngày? (Biết năng suất của mỗi người như nhau).
Lời giải:
1 người làm công việc đó trong số ngày là:
45 × 14 = 630 (ngày)
Vậy có 70 người thì làm xong trong số ngày là:
630 : 70 = 9 (ngày)
Đáp số: 9 ngày.
Câu 43: Số A chia cho 21 dư 7. Hỏi a phải thay đổi thế nào để được phép chia không còn dư và thương giảm đi 3 đơn vị (Số chia vẫn là 21).
Lời giải:
Gọi thương của phép chia là B
A : 21 = B (dư 7)
A = B × 21 + 7
Nếu bớt A đi 7 đơn vị thì phép chia trở thành phép chia hết và thương không đổi.
Nếu thương giảm đi 3 đơn vị, số bị chia cần giảm tiếp là 3 × 21 = 63 đơn vị
Vậy số bị chia cần giảm đi là: 7 + 63 = 70 đơn vị.
Câu 44: Tìm ƯCLN của 2n – 1 và 9n + 4 (n thuộc ℕ).
Lời giải:
Gọi d = (2n – 1; 9n + 4) ⇒ 2n – 1; 9n + 4 chia hết cho d
⇒ 2(9n + 4) – 9(2n – 1) = 18n + 8 – 18n + 9 = 17 chia hết cho d
⇒ d = 1 hoặc d = 17
Nếu 1 trong 2 số 2n – 1; 9n + 4 chia hết cho 17 thì ƯCLN(2n – 1; 9n + 4) = 17.
Nếu 1 trong 2 số 2n – 1; 9n + 4 không chia hết cho 17 thì ƯCLN(2n – 1; 9n + 4) = 1.
Câu 45: Để lát một căn phòng hình chữ nhật có chiều dài 12m, chiều rộng 8m, người ta dùng gạch men hình vuông có cạnh 4 dm. Hỏi cần bao nhiêu viên gạch để lát kín căn phòng đó?
Lời giải:
Diện tích căn phòng đó là: 12 . 8 = 96 (m²)
Diện tích một viên gạch là: 40 . 40 =1600 (cm²)
Đổi: 1600 cm² = 0,16m²
Số gạch dùng để lát nền là: 96 : 0,16 = 600 (viên).
Đáp số: 600 viên gạch.
Câu 46: Tính (272 . 92 – 1715 : 195) : 20192018.
Lời giải:
Ta có: (272 . 92 – 1715 : 195) : 20192018
= [(27.9)2 – (171 : 19)5] : 20192018
= (2432 – 95) : 20192018
= (59 049 – 59 049) : 20192018
= 0.
Câu 47: Giá bán một chiếc áo khoác là 350 000 đồng. Nhân dịp Nô-en, cửa hàng giảm giá 10% cho khách hàng. Hỏi khách hàng mua chiếc áo đó thì còn phải trả bao nhiêu tiền?
Lời giải:
Khách hàng mua chiếc áo đó phải trả số tiền là:
350 000 – (350 000 × 10%) = 315 000 (đồng)
Đáp số: 315 000 đồng
Câu 48: Một cửa hàng bán 1 cái quần với giá 350 000 đồng. Nay giảm 30% giá bán. Hỏi người mua cái quần phải trả bao nhiêu tiền?
Lời giải:
Khách hàng mua chiếc quần đó phải trả số tiền là:
350 000 – (350 000 × 30%) = 245 000 (đồng)
Đáp số: 245 000 đồng.
Câu 49: Tính nhanh: 17 × 26 + 26 × 44 + 39 × 26.
Lời giải:
17 × 26 + 26 × 44 + 39 × 26
= 26 × (17 + 44 + 39)
= 26 × 100
= 2 600.
Câu 50: Viết số thích hợp vào chỗ chấm:
2 ha = …. m2
39 678 m2 = …. ha … m2
978 m2 = …. ha
690 000 m2 = …. ha
Lời giải:
2 ha = 20 000 m2
39 678 m2 = 3 ha 9678 m2
978 m2 = 0,0978 ha
690 000 m2 = 69 ha
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.