Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 26) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 26)
a) 372,95 : 3.
b) 757,5 : 35.
c) 431,25 : 125.
d) 35,1 × 8,5.
Lời giải:
a) 372,95 : 3 = 124,316666666….
b) 757,5 : 35 = 21,6428571…
c) 431,25 : 125 = 3,45.
d) 35,1 × 8,5 = 298,35.
Câu 2: Phân tích thành nhân tử 5(x + 3y) – 15x(x + 3y).
Lời giải:
5(x + 3y) – 15x (x + 3y)
= (x + 3y)(5 – 15x)
= 5(x + 3y)(1 – 3x).
Câu 3: Phân tích thành nhân tử
a) 5(x + 3y) – 15x(x + 3y);
b) 2(x + 1)2 – y(x + 1);
c) xy(x + y)2 – y(x + y);
d) xy(x – y) – 2x + 2y.
Lời giải:
a) Ta có: 5(x + 3y) – 15x(x + 3y)
= (x + 3y)(5 – 15x)
= 5(x + 3y)(1 – 3x).
b) Ta có: 2(x + 1)2 – y(x + 1)
= (x + 1)[2(x + 1) – y]
= (x + 1)(2x + 2 – y).
c) Ta có: xy(x + y)2 – y(x + y)
= y(x + y)[x(x + y) – 1]
= y(x + y)(x2 + xy – 1).
d) Ta có: xy(x – y) – 2x + 2y
= xy(x – y) – 2(x – y)
= (x – y)(xy – 2).
Câu 4: Cho 5 điểm A, B, C, D, E. Chứng minh rằng:
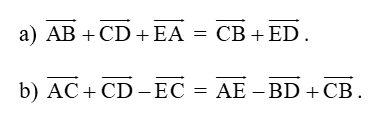
Lời giải:
a) Ta có:

Vậy →AB+→CD+→EA = →CB+→ED
b) Ta có:
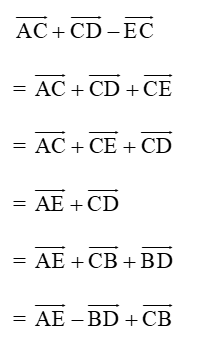
Vậy →AC+→CD−→EC = →AE−→BD+→CB .
Câu 5: Cho các số a, b, c khác nhau đôi một và thoả mãn a2 – 2b = b2 – 2c = c2 – 2a.
Tính giá trị của biểu thức A = (a + b + 2)(b + c + 2)(c + a + 2).
Lời giải:
Ta có: a2 – 2b = c2 – 2a
⇔ a2 – c2 = 2b – 2a
⇔ (a – c)(a + c) = 2(b – a)
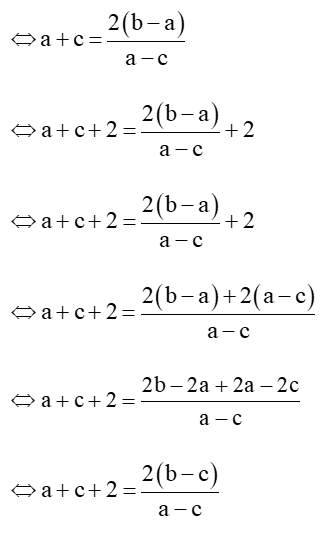
Chứng minh tương tự ta có:
a+b+2=2(a−c)a−b và b+c+2=2(b−a)b−c
Suy ra A = (a + b + 2)(b + c + 2)(c + a + 2)
=2(a−c)a−b.2(b−a)b−c.2(b−c)a−c=−8
Vậy A = – 8.
Lời giải:
Ta có x2 ≤ 4
⟹ – 2 ≤ x ≤ 2
⟹ A = [– 2; 2]
Ta có x < 1
⟹ B = (– ∞; 1)
Vậy:
A ∪ B = (– ∞; 2];
A ∩ B = [– 2; 1);
A ∖ B = [1; 2];
CRB = [1; + ∞).
A. A ⊂ B
B. C ⊂ A
C. D ⊂ B
D. D ⊂ C.
Lời giải:
Đáp án đúng là: A
Vì x2 + 4 > 0 ∀x ∈ R nên A = ∅.
(x2 – 4)(x2 + 1) = 0 ⇔ (x2 – 4) = 0 ⇔ x = ±2 nên B = {– 2; 2}.
|x| < 2 ⇔ – 2 < x < 2 nên D = (– 2; 2).
=> A ⊂ B = C ⊂ D.
Vậy ta chọn đáp án A.

Lời giải:
Chiều rộng mảnh đất là: 1,5 + 2,5 = 4 (m)
Chiều dài mảnh đất là: 24 : 4 = 6 (m)
Diện tích trồng hoa là: S=12.6.2,5=7,5 (m2) .
Vậy diện tích trồng hoa là 7,5 m2.
Câu 9: Cho a, b, c là ba cạnh của một tam giác. Chứng minh rằng:
A=ab + c - a+ba + c - b+ca + b - c≥3.
Lời giải:
Vì a, b, c là ba cạnh của một tam giác
Nên ab + c - a>0,ba + c - b>0,ca + b - c>0
Ta có:
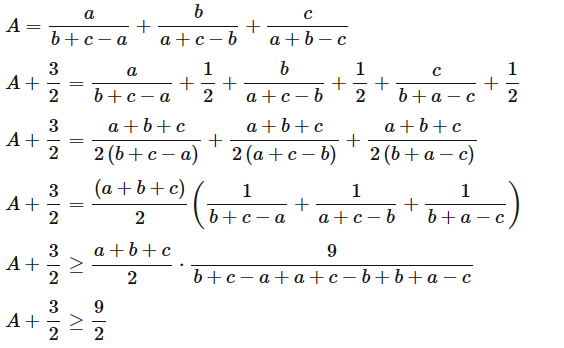
Hay A ≥ 3
Vậy A ≥ 3.
Lời giải:
Nửa chu vi mảnh đất là: 100 : 2 = 50 (m)
Gọi chiều rộng của mảnh đất là x (m) (0 < x < 50)
Chiều dài của mảnh đất là: 50 – x (m)
Vì chiều dài gấp 4 lần chiều rộng nên ta có phương trình :
50 – x = 4x ⇔ 5x = 50 ⇔ x = 10 (thỏa mãn)
Nên chiều dài của mảnh đất là: 4 . 10 = 40 (m)
Diện tích của mảnh đất là:
10 . 40 = 400 ( m2)
Số tiền của mảnh đất đó là :
15 x 400 = 6000 ( triệu đồng) = 6 tỷ đồng
Vậy giá tiền của mảnh đất đó là 6 tỷ đồng.
Lời giải:
Nửa chu vi mảnh đất là: 100 : 2 = 50 (m)
Gọi chiều rộng của mảnh đất là x (m) (0 < x < 50)
Chiều dài của mảnh đất là: 50 – x (m)
Vì 5 lần chiều rộng hơn 2 lần chiều dài 40m nên ta có phương trình :
5x – 2(50 – x) = 40
⇔ 5x – 100 + 2x = 40
⇔ 7x = 140
⇔ x = 20 (thỏa mãn)
Nên chiều dài của mảnh đất là : 50 – 20 = 30 (m)
Vậy chiều rộng của miếng đất là 20 m, chiều dài của mảnh đất là 30 m.
Câu 12: Cho tam giác ABC. Tìm điểm M thỏa mãn điều kiện: →MA−→MB+→MC=→0
Lời giải:
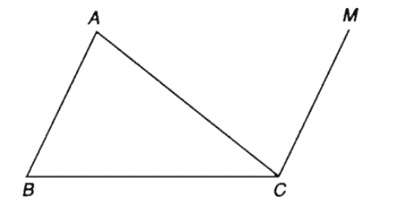
Ta có: →MA−→MB+→MC=→0
⇔→BA=→CM
Suy ra M là tập hợp các điểm đi qua C và song song với AB
Hay M là đỉnh của hình bình hành ABCM
Vậy M là đỉnh của hình bình hành ABCM.
Câu 13: Tìm tọa độ điểm M thỏa mãn: →MA−→MB+→MC=→0
A. M(2; 2);
B. M(– 2 ; – 1);
C. M(– 1; – 2);
D. M(– 2; – 2).
Lời giải:
Đáp án đúng là: C
Gọi M(x; y)
Suy ra {→MA=(−1−x;3−y)→MB=(2−x;4−y)→MC=(2−x;−1−y) ⇒→MA−→MB+→MC=(−1−x;−2−y)
Mà →MA−→MB+→MC=→0
Nên {−1−x=0−2−y=0⇔{x=−1y=−2
Suy ra M (– 1; – 2)
Vậy ta chọn đáp án C.
Câu 14: Chứng minh sin 3x = 3sin x – 4sin3x, cos 3x = 4cos3x – 3cos x
Lời giải:
Ta có: sin 3x = sin (2x + x) = sin 2x . cos x + cos 2x . sin x
= (2sin x. cos x) . cos x + (1 – 2sin2x) . sin x
= 2sin x. cos2 x + sin x – 2 sin3x
= 2sin x . (1 – sin2x) + sin x – 2 sin3x
= 2sin x – 2 sin3x + sin x – 2 sin3x
= 3sin x – 4sin3x
Vậy sin 3x = 3sin x – 4sin3x
Ta có: cos 3x = cos (2x + x) = cos 2x . cos x – sin 2x . sin x
= (–1 + 2cos2x) . cos x – 2cos x . sin x . sin x
= – cos x + 2cos3 x – 2cos x . sin2 x
= – cos x + 2cos3 x – 2cos x . (1 – cos2 x)
= – cos x + 2cos3 x – 2cos x + 2cos3 x
= 4cos3x – 3cos x
Vậy cos 3x = 4cos3x – 3cos x .
Câu 15: So sánh giá trị của biểu thức A và B biết
A=¯a,65+¯4,bc; B=¯a,b+3,5+¯1,2c .
Lời giải:
Ta có
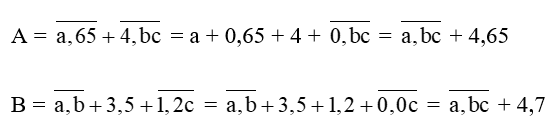
Vì 4,65 < 4,7 nên A < B
Vậy A < B.
Lời giải:
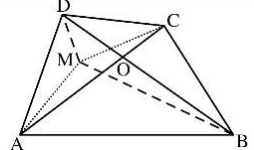
Gọi O là giao điểm của AC và BD
+) Trường hợp 1: O ≡ M
Ta có MA + MB + MC + MD = OA + OB + OC + OD = AC +BD (1)
+) Trường hợp 2: O ≠ M
Xét tam giác AMC có AC ≤ AM + MC (bất đẳng thức trong tam giác)
Xét tam giác MBD có BD ≤ BM + MB (bất đẳng thức trong tam giác)
Suy ra MA + MB + MC + MD ≥ AC + BD (2)
Từ (1) và (2) suy ra MA + MB + MC + MD ≥ AC + BD
Dấu “ = ” xảy ra khi O ≡ M
Vậy tổng các khoảng cách từ M đến các đỉnh tứ giác nhỏ nhất khi M là giao điểm của AC và BD.
Câu 17: Giải phương trình: x5 = x4 + x3 + x2 + x +2
Lời giải:
Ta có: x5 = x4 + x3 + x2 + x +2
⇔ x5 – 1 = x4 + x3 + x2 + x +1
⇔ (x – 1) . (x4 + x3 + x2 + x +1) = x4 + x3 + x2 + x +1
⇔ (x – 2) . (x4 + x3 + x2 + x +1) = 0 (*)
Vì x4 + x3 + x2 + x +1
=(x4+2x2.x2+x24)+(x24+2.x2.1+1)+x22=(x2+x2)2+(x2+1)2+x22>0
Do đó (*) ⇔ x – 2 = 0
⇔ x = 2
Vậy phương trình có nghiệm là x = 2.
Câu 18: Phân tích đa thức sau thành nhân tử:
x5 – x4 – x3 – x2 – x – 2
Lời giải:
Ta có: x5 – x4 – x3 – x2 – x – 2
= x5 + x4 – 2x4 + x3 – 2x3 + x2 – 2x2 + x – 2x – 2
= (x5 – 2x4) + (x4 – 2x3) + (x3 – 2x2) + (x2 – 2x) +(x – 2)
= x4(x – 2) + x3(x – 2) + x2(x – 2) + x(x – 2) + (x – 2)
= (x – 2) . (x4 + x3 + x2 + x +1)
Vậy x5 – x4 – x3 – x2 – x – 2 = (x – 2) . (x4 + x3 + x2 + x +1)
Câu 19: Phân tích đa thức sau thành nhân tử bằng nhiều cách: x3 – 7x – 6.
Lời giải:
Cách 1: x3 – 7x – 6
= x3 + x2 – x2 – x – 6x – 6
= x2(x + 1) – x(x + 1) – 6(x + 1)
= (x + 1)(x2 – x – 6)
= (x + 1)(x2 + 2x – 3x – 6)
= (x + 1)[x(x + 2) – 3(x + 2)]
= (x + 1)(x + 2)(x – 3).
Cách 2: x3 – 7x – 6
= x3 – x – 6x – 6
= x(x2 – 1) – 6(x + 1)
= x(x – 1)(x + 1) – 6(x + 1)
= (x + 1)[x(x – 1) – 6]
= (x + 1)(x2 – x – 6)
= (x + 1)(x2 + 2x – 3x – 6)
= (x + 1)[x(x + 2) – 3(x + 2)]
= (x + 1)(x + 2)(x – 3).
Câu 20: Phân tích đa thức thành nhân tử:
a) 5a – 10ax – 15a.
b) – 2a2b – 4ab2 – 6ab.
c) 3a2x – 6a2y + 12a.
Lời giải:
a) 5a – 10ax – 15a
= 5a + 5ax – 15ax – 15a
= 5a(1 + x) – 15a(x + 1)
= (1 + x)(5a – 15a)
= – 10a(1 + x)
b) – 2a2b – 4ab2 – 6ab
= – (2a2b + 4ab2 + 6ab)
= – 2ab(a + 2b + 3)
c) 3a2x – 6a2y + 12a
= 3a(ax – 2ay + 4)
Gọi thời gian làm một mình xong công việc của lớp 9A là x (giờ)
Thời gian làm một mình xong công việc của lớp 9B là y (giờ)
Đổi 1 giờ 20 phút = 43 giờ
Trong 43 giờ lớp 9A làm được 43x công việc
Trong 43 giờ lớp 9B làm được 43y công việc
Suy ra 43x+43y=1 (1)
Thời gian lớp 9A làm nửa công việc là 12x
Thời gian lớp 9B làm nửa công việc là 12y
Suy ra 12x+12y=3 (2)
Từ (1) và (2) ta có hệ phương trình:
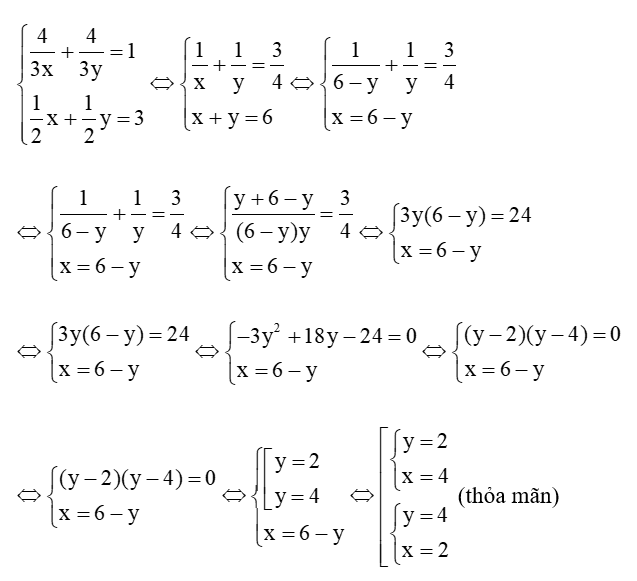
Vậy nếu làm một mình lớp 9A sau 4 giờ hoàn thành công việc, lớp 9B sau 2 giờ hoàn thành công việc hoặc lớp 9A sau 2 giờ hoàn thành công việc, lớp 9B sau 4 giờ hoàn thành công việc.
Lời giải:
Ta có n(Ω) = C312 = 220
a) Gọi biến cố A: “ trong 3 bóng lấy ra có ít nhất 2 bóng tốt ”
+) Trong 3 bóng có 2 bóng tốt, 1 bóng không tốt: C15.C27
+) Trong 3 bóng có 3 bóng tốt: C37
Suy ra n(A) = C15.C27 + C37 = 140
Vậy xác suất để lấy được ít nhất 2 bóng tốt là P(A)=140220=711 .

Lời giải:
Đáp án đúng là: C
Trong 3 bóng có 1 bóng hỏng
Ta có n(Ω)=C312=220
Gọi biến cố A: “ trong 3 bóng lấy ra có 1 bóng hỏng ”
Ta có n(A)=C14.C28=112
Suy ra P(A)=112220=2855 .
Vậy ta chọn đáp án C.
Câu 24: Tìm m để phương trình 2x2 + (m + 1)x + m – 8 = 0 có nghiệm.
Lời giải:
Phương trình 2x2 + (m + 1)x + m – 8 = 0 (1) là phương trình bậc hai một ẩn có:
a = 2, b = m + 1, c = m – 8 (m là tham số)
∆ = (m + 1)2 – 4 . 2 . (m – 8) = m2 + 2m + 1 – 8m + 64 = m2 – 6m + 65
Để phương trình (1) có nghiệm khi và chỉ khi ∆ ≥ 0 ⇔ m2 – 6m + 65 ≥ 0
Xét tam thức bậc hai m2 – 6m + 65 có:
∆m = (– 6)2 – 4 . 1 . 65 = – 224 < 0 và hệ số am = 1 > 0
Sử dụng định lí về dấu của tam thức bậc hai, tam thức m2 – 6m + 65 mang dấu dương với mọi m ∈ ℝ
Do đó m2 – 6m + 65 > 0 với mọi số thực m
Vậy phương trình đã cho luôn có nghiệm với mọi giá trị thực của m.
Câu 25: Tìm tất cả các cặp số (x, y) thỏa mãn:
5x−2√x(y+2)+y2+1=0.
Lời giải:
Điều kiện xác định: x ≥ 0
Ta có 5x−2√x(y+2)+y2+1=0
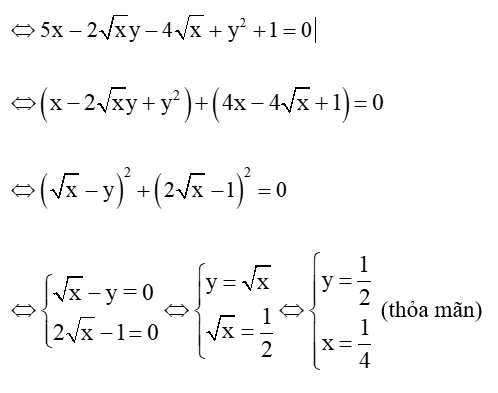
Vậy (x;y)=(14;12) .
Câu 26: Đồ thị hàm số y = x3 – 4x + 3 cắt trục hoành tại điểm có hoành độ bằng?
Lời giải:
Đồ thị hàm số y = x3 – 4x + 3 cắt trục hoành nên y = 0
Suy ra x3 – 4x + 3 = 0
⇔ x3 – x2 + x2 – x – 3x + 3 = 0
⇔ x(x2 – 1) + x( x – 1) – 3(x – 1) = 0
⇔ x(x – 1)(x + 1) + x( x – 1) – 3(x – 1) = 0
⇔ (x – 1)[x(x + 1) + x – 3] = 0
⇔ (x – 1)(x2 + x – 3) = 0
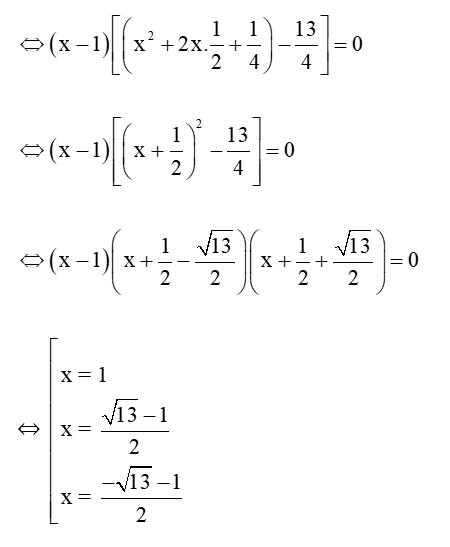
Vậy đồ thị hàm số x3 – 4x + 3 cắt trục hoành tại các điểm (1; 0), (√13−12;0) , (−√13−12;0) .
Câu 27: Đồ thị hàm số y = x4 – x3 – 2 cắt trục hoành tại bao nhiêu điểm?
A. 1
B. 2
C. 0
D. 4.
Lời giải:
Đáp án đúng là: B
y = x4 – x3 – 2
y’ = 4x3 – 3x2 = 0 ⇔ x2(4x – 3) = 0 ⇔[x=0x=34
Ta có bảng biến thiên:
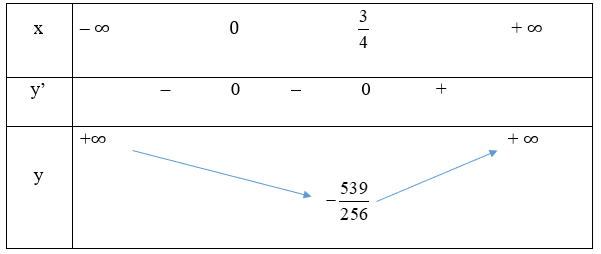
Quan sát bảng ta thấy số giao điểm của đồ thị hàm số với trục hoành là 2
Vậy ta chọn đáp án B.
Lời giải:
Người bán bò lãi số tiền là:
15 – 10 + 17 – 20 = 2 (triệu đồng)
Vậy người bán bò lãi 2 triệu đồng.
Lời giải:
Gọi M’ (x’; y’) thuộc d’ là ảnh của M(x; y) thuộc d
Qua phép tịnh tiến theo vectơ →v=(2;3)
⇒{x'=x+2y'=y+3⇒{x=x'−2y=y'−3
Vì M(x; y) thuộc d nên 3x – 5y + 3 = 0
⇔ 3(x’ – 2) – 5(y’ – 3) + 3 = 0
⇔ 3x’ – 5y’ – 3 +12 = 0
Vậy phương trình đường thẳng d’ là 3x’ – 5y’ – 3 +12 = 0.
A. △’: x + 2y + 2 = 0
B. △’: x + 2y – 3 = 0
C. △’: x + 2y + 1 = 0
D. △’: x + 2y = 0
Lời giải:
Đáp án đúng là: D
Vì △’ // △ nên phương trình đường thẳng △’ có dạng x + 2y + c = 0
Lấy A(1; 0) thuộc △, khi đó
T→v(A)=A'⇔{xA'=1+1=2yA'=0−1=−1⇒A'(2;−1)
Vì A’ ∈ △’ nên 2 + 2 . (–1) + c = 0
Suy ra c = 0
Do đó phương trình đường thẳng △’ là x + 2y = 0
Vậy ta chọn đáp án D.
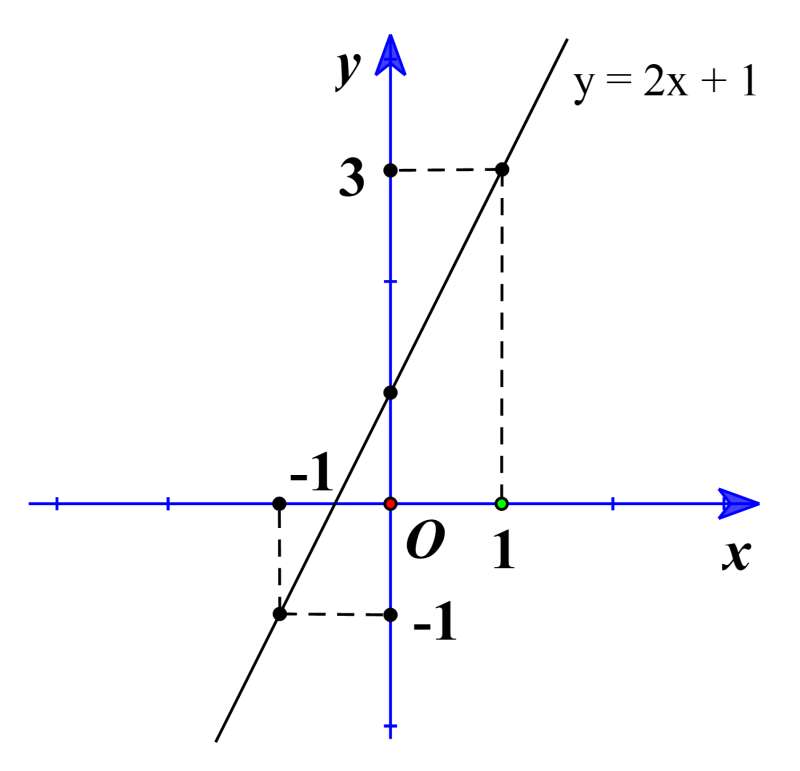
Câu 31: Cho hàm số y = (2 – m)x + m + 1 (với m là tham số và m ≠ 2) có đồ thị là đường thẳng d.
a) Khi m = 0, hãy vẽ d trên trục tọa độ Oxy.
b) Tìm m để d cắt đường thẳng y = 2x – 5 tại điểm có hoành độ bằng 2.
c) Tìm m để d cùng với các trục tọa độ Ox, Oy tạo thành một tam giác có diện tích bẳng 2.
Lời giải:
a) Khi m = 0 thì d có dạng y = 2x + 1
Bảng giá trị:
|
x |
–1 |
0 |
1 |
|
y |
–1 |
1 |
3 |
Ta có đường thẳng d đi qua hai điểm A(0; 1) và B(−12;0)
b) Thay x = 2 vào y = 2x – 5 ta có
y = 2 . 2 – 5 = – 1
Thay x = 2, y = – 1 vào d ta có
– 1 = (2 – m). 2 + m + 1
⇔ – 1 = 4 – 2m + m + 1
⇔ m = 6 (thỏa mãn)
Khi m = 6 thì d có dạng y = – 4x + 7 cắt đường thẳng y = 2x – 5
Vậy m = 6 thì d cắt đường thẳng y = 2x – 5 tại điểm có hoành độ bẳng 2.
c) Vì m ≠ 2 nên d cắt Ox tại điểm C(m+1m−2;0) và cắt Oy tại điểm D(0; m + 1)
Ta có SCOD = = 2 12|m+1m−2||m+1|
⇔ (m + 1)2 = 4 |m−2|
⇔[(m+1)2=4(m−2)(m+1)2=4(2−m)⇔[m2+2m+1=4m−8m2+2m+1=8−4m⇔[m2−2m+9=0m2+6m−7=0⇔[m2−2m+9=0(m−1)(m+7)=0
⇔[m=1m=−7(thỏa mãn)
Vậy m = 1 hoặc m = – 7 thì d cùng với các trục tọa độ Ox, Oy tạo thành một tam giác có diện tích bẳng 2.
Câu 32: Cho hai đường thẳng (d1): y = 2x + 5 và (d2): y = (m + 1)x + m – 1
Tìm m để hai đường thẳng cắt nhau tại điểm của tung độ bằng 1.
Lời giải:
Thay y = 1 vào (d1): y = 2x + 5 ta có
1 = 2x + 5 ⇔ x = – 2
Thay x = – 2, y = 1 vào (d2) ta có
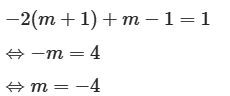
Vậy với m = – 4 thì hai đường thẳng cắt nhau tại điểm có tung độ bằng 1.
Lời giải:
Gọi d là đường thẳng qua H(0; 4) và song song với trục Ox
Vì d // Ox nên phương trình đường thẳng d có dạng y = b (b ≠ 0)
Vì H(0; 4) thuốc đường thẳng d
Nên b = 4
Suy ra (d): y = 4
Phương trình hoành độ giao điểm của d và y = –2x là
–2x = 4 ⇔ x = –2
Suy ra y = 4
Do đó A(–2; 4)
Phương trình hoành độ giao điểm của d và y = x là x = 4
Suy ra y = 4
Do đó B(4; 4)
Vậy A(–2; 4) và B(4; 4).
Lời giải:
Đường thẳng (d) song song với trục Ox và đi qua điểm K(0; 2) nên nó là đường thẳng y = 2
Đường thẳng y = 2 cắt đường thẳng (1) tại A nên điểm A có tung độ bằng 2
Thay y = 2 vào phương trình y = – 2x ta được x = – 1
Vậy điểm A(– 1; 2)
Đường thẳng y = 2 cắt đường thẳng (2) tại B nên điểm B có tung độ bằng 2
Thay y = 2 vào phương trình y = 0,5x ta được x = 4
Vậy điểm B(4; 2).
Câu 35: Tính tổng N = 1 + 11 + 111 + 1111 +....+ 11...1 (có n chữ số 1)
Lời giải:
Ta có N = 1 + 11 + 111 +....+ 11...1
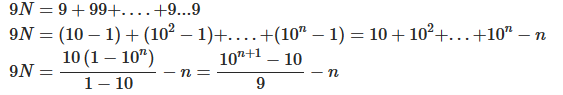
Suy ra N = 19(10n+1−109−n)
Vậy N = 19(10n+1−109−n) .
A = 1 + 11 + 111 + 1111 + ... + 11...1 (10 chữ số 1)
Lời giải:
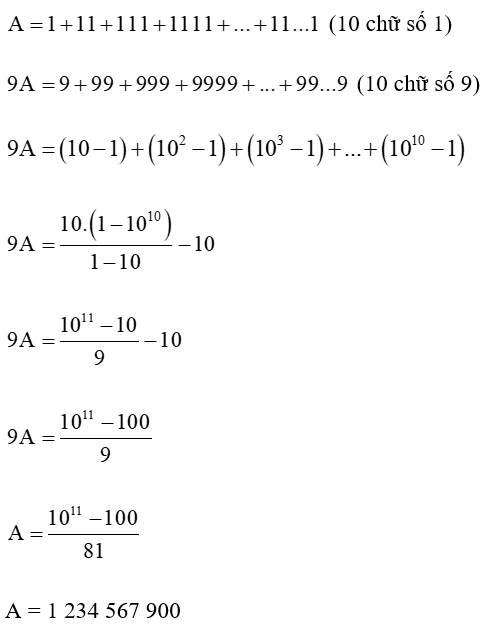
Vậy A = 1 234 567 900.
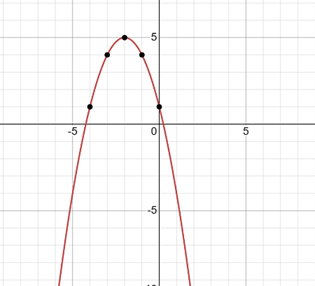
Câu 37: Lập bảng biến thiên và vẽ đồ thị hàm số y = – x2 – 4x + 1
Lời giải:
Tập xác định D = R
Bảng biến thiên :
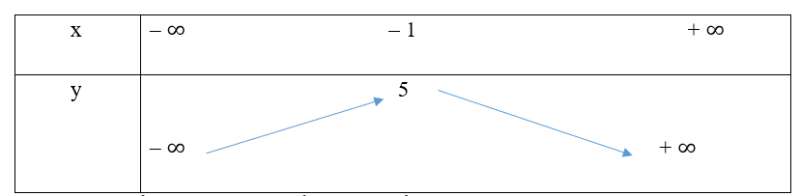
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = y = – x2 – 4x + 1 là một parabol (P):
– Có đỉnh S với hoành độ xS = – 2, tung độ yS = 5;
– Có trục đối xứng là đường thẳng x = – 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay xuống dưới vì a = – 2 < 0;
– Cắt trục tung tại điểm có tung độ bằng 1, tức là đồ thị đi qua điểm có tọa độ (0; 1);
– Ngoài ra, đồ thị hàm số y = f(x) còn đi qua hai điểm (– 1; 4) và (– 4; 1)
Ta vẽ được đồ thị như hình dưới:
a) Chứng minh rằng MNPQ là hình bình hành.
b) Xác định vị trí O để MNPQ là hình chữ nhật.
Lời giải:
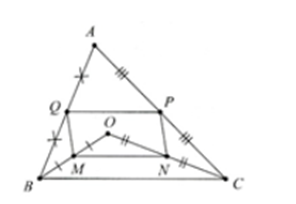
a) Xét tam giác ABO có Q là trung điểm của AB, M là trung điểm của OB
Suy ra QM là đường trung bình
Suy ra QM // AO, QM = 12AO (1)
Xét tam giác ACO có P là trung điểm của AC, N là trung điểm của OC
Suy ra PN là đường trung bình
Suy ra PN // AO, PN = 12AO (2)
Từ (1) và (2) suy ra QM // PN, QM = PN
Do đó MNPQ là hình bình hành
Vậy MNPQ là hình bình hành
b) Xét tam giác ABC có P là trung điểm của AC, Q là trung điểm của AB
Suy ra PQ là đường trung bình
Suy ra PQ // BC
Để hình bình hành MNPQ là hình chữ nhật
⇔ QM ⊥ QP
⇔ QM ⊥ BC (vì QP // BC)
⇔ AO ⊥ BC (vì QM // AO)
⇔ O thuộc đường thẳng qua A và vuông góc BC
Vậy O thuộc đường thẳng qua A và vuông góc BC thì MNPQ là hình chữ nhật.
Câu 39: Cho đường tròn (O; R) đường kính AB và tiếp tuyến Ax. Từ điểm C thuộc Ax kẻ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm). Gọi giao
điểm của CO và AD là I.
a) Chứng minh: CO ⊥ AD.
b) Gọi giao điểm của CB và đường tròn (O) là E (E ≠ B). Chứng minh CE . CB = CI . CO.
c) Chứng minh: Trực tâm H của tam giác CAD di động trên đường cố định khi
điểm C di chuyển trên Ax.
Lời giải:
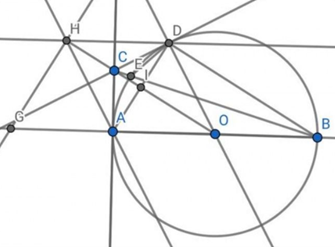
a) Vì C là giao điểm của 2 tiếp tuyến CA và CD
Nên CA = CD
Suy ra C thuộc đường trung trực của AD (1)
Vì A, D cùng thuộc (O) nên OA = OD
Suy ra O thuộc đường trung trực của AD (2)
Từ (1) và (2) suy ra CO ⊥ AD
b) Xét tam giác vuông ACO có CO ⊥ AI
Suy ra CI . CO = AC2 (hệ thức lượng trong tam giác vuông)
Vì tam giác AEB nội tiếp (O), AB là đường kính
Nên tam giác AEB vuông tại E
Suy ra AE ⊥ BE
Xét tam giác vuông ACB có AE ⊥ BC
Suy ra CE . CB = AC2 (hệ thức lượng trong tam giác vuông)
Mà CI . CO = AC2 (chứng minh trên)
Suy ra CE . CB = CI . CO
Vậy CE . CB = CI . CO
c) Vì H là trực tâm tam giác ACD nên AH ⊥ CD, AC ⊥ DH, CH ⊥ AD
Vì AC ⊥ DH, AC ⊥ AB nên DH // AB
Vì AH ⊥ CD, DO ⊥ CD nên AH // DO
Xét tứ giác AHDO có AH // DO, DH // AO (chứng minh trên)
Suy ra AHDO là hình bình hành
Mà AD cắt HO tại I
Do đó I là trung điểm của HO
Trên tia đối của tia AO lấy G sao cho GA = AO
Xét tam giác GHO có A là trung điểm của OG, I là trung điểm của HO
Nên AI là đường trung bình
Suy ra AI // GH
Mà AI ⊥ CO nên GH ⊥ CO
Suy ra ^OHG=90°
Do đó H thuộc đường tròn đường kính OG
Vậy khi C di chuyển trên Ax thì H di chuyển trên đường tròn tâm A bán bính AO cố định.
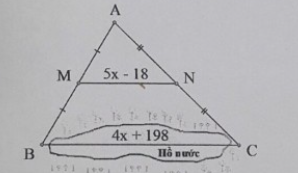
Lời giải:
Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC
Suy ra MN là đường trung bình
Do đó MN = BC
Mà MN = 5x – 18 (mét); BC = 4x + 198 (mét)
Suy ra
⇔ 5x – 18 = 2x + 99
⇔ 3x = 117
⇔ x = 39
Suy ra BC = 4 . 39 + 198 = 354 (mét)
Vậy khoảng cách BC trong hình vẽ là 354 mét.
Câu 41: Chứng minh 1 . 2 + 2 . 5 + 3 . 8 + .... + n(3n – 1) = n2 (n+1) với mọi n thuộc N*.
Lời giải:
1 . 2 + 2 . 5 + 3 . 8 + .... + n(3n – 1) = n2 (n + 1) (*)
+) Với n = 1
Vế trái của (*) = 2, vế phải của (*) = 12 (1 + 1 ) = 2
Suy ra (*) đúng với n = 1
Giả sử (*) đúng với n = k (k ∈ N*) , ta có:
1 . 2 + 2 . 5 + ... + k(3k – 1) = k2(k + 1) (1)
Ta chứng minh (*) đúng với n = k + 1, thật vậy:
1 . 2 + 2 . 5 + ... + k(3k – 1) + (k + 1)[3(k + 1) – 1] = k2 (k + 1) + (k + 1)[3(k + 1) – 1]
⇔ 1 . 2 + 2 . 5 + ... + k(3k – 1) + (k + 1)[3(k + 1) –1] = (k + 1)(k2 + 3k +2)
⇔ 1 . 2 + 2 . 5 + ... + k(3k – 1) + (k + 1)[3(k + 1) –1] = (k + 1)(k2 + k + 2k + 2)
⇔ 1 . 2 + 2 . 5 + ... + k(3k – 1) + (k + 1)[3(k + 1) –1] = (k + 1)[k(k + 1) + 2(k +1)]
⇔ 1 . 2 + 2 . 5 + ... + k(3k – 1) + (k + 1)[3(k + 1) –1] = (k + 1)2(k + 2)
Suy ra (*) đúng với n = k + 1 , theo nguyên lý qui nạp (*) đúng với mọi n thuộc N*
Vậy 1 . 2 + 2 . 5 + 3 . 8 + .... + n(3n – 1) = n2 (n+1) với mọi n thuộc N* .
Sn = 1 . 2 + 2 . 5 + 3 . 8 + ....... + n(3n – 1).
Lời giải:
Ta có n(3n – 1) = 3n2 – n
Với n = 1 ta có 1 . 2 = 3 . 12 – 1
Với n = 2 ta có 2 . 5 = 3 . 22 – 2
Với n = 3 ta có 3 . 8 = 3 . 32 – 3
....
Với n = n ta có n(3n – 1) = 3n2 – n
Cộng vế các đẳng thức ta được
1 . 2 + 2 . 5 + 3 . 8 + ....... + n(3n – 1) = 3(12 + 22 + ... + n2) – (1 + 2 + ... + n)
⇔ Sn =
⇔ Sn =
Vậy Sn = n2(n + 1).
Câu 43: Tìm số tự nhiên n sao cho: n2 + 3n + 6 chia hết n + 3
Lời giải:
Ta có:
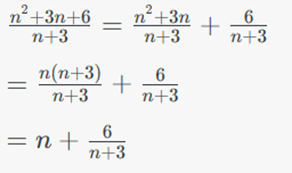
Để n2 + 3n + 6 chia hết n + 3 thì 6 chia hết cho n + 3
Suy ra n + 3 ∈ Ư(6) = { 1; 2; 3; 6; – 1 ; – 2; – 3– 6}
Với n + 3 = 1 thì n = – 2 (loại)
Với n + 3 = 2 thì n = – 1 (loại)
Với n + 3 = 3 thì n = 0 (thỏa mãn)
Với n + 3 = 6 thì n = 3 (thỏa mãn)
Với n + 3 = – 1 thì n = – 4 (loại)
Với n + 3 = – 2 thì n = – 5 (loại)
Với n + 3 = – 3 thì n = – 6 (loại)
Với n + 3 = – 6 thì n = – 9 (loại)
Vậy n = 0, n = 3.
Câu 44: Tìm m để phương trình : x2 – 2mx + m – 1 = 0 có 2 nghiệm thỏa mãn x1 < 1 < x2.
Lời giải:
Áp dụng hệ thức Vi – et ta có:
Theo bài, x1 < 1 < x2 ⇔ (x1 – 1)(x2 – 1) < 0
⇔ x1 . x2 – x1 – x2 + 1 < 0
⇔ 2m – (m – 1) + 1 < 0
⇔ m + 2 < 0
⇔ m < – 2
Vậy m < – 2 thì phương trình đã cho có hai nghiệm thỏa mãn x1 < 1 < x2.
Lời giải:
Xét phương trình: (m + 1)x2 – 2(m – 1)x + m – 2 = 0 (1).
Để phương trình (1) có hai nghiệm x1, x2 thì (*)
Ta có △’ = b’2 – ac
= [–(m – 1)]2 – (m + 1)(m – 2)
= m2 – 2m + 1 – m2 + m + 2
= 3 – m
Do đó
Theo hệ thức Vi – ét ta có
Theo bài,
⇔ 8(m – 1) = 7(m – 2)
⇔ 8m – 8 = 7m – 14
⇔ m = – 6 (thỏa mãn)
Vậy m = – 6 thì phương trình có nghiệm x1, x2 thỏa mãn .
Câu 46: Cho tam giác ABC đều cạnh 2a. Khi đó độ dài vectơ bằng
A. 2a;
B. 2a ;
C. 4a;
D. a .
Lời giải:
Đáp án đúng là B
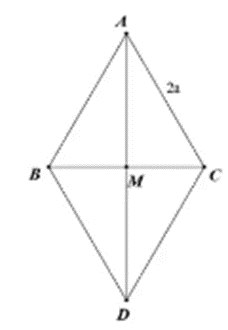
Ta có
![]()
Vậy ta chọn đáp án B.
Câu 47: Tính: 1 + 2 + 3 + ... + 99 + 100.
Lời giải:
1 + 2 + 3 + ... + 99 + 100
= ( 1 + 99 ) + ( 2 + 98 ) + ( 3 + 97 ) + ...... + 100
= 100 + 100 + 100 + ...... + 100 ( 50 số 100 )
= 100 x 50
= 5000
Vậy 1 + 2 + 3 + ... + 99 + 100 = 5000.
Câu 48: Giải phương trình : cos4 x + sin4 x = cos2x.
Lời giải:
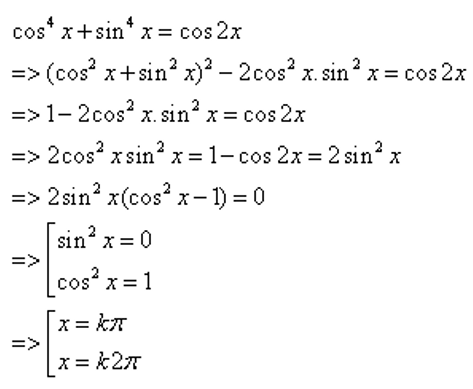
Vậy x = kπ, x = k2π.
a) cos4 x – sin4 x = cos2x.
b) cos4 x + sin4 x = cos 4x.
c) = tanx.
Lời giải:
a) Ta có:
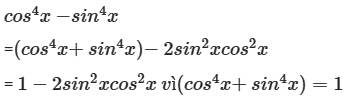
= cos2x
Vậy cos4 x – sin4 x = cos2x.
b) Ta có: cos4 x + sin4 x
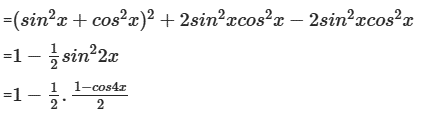
= 1 –
= cos 4x
Vậy cos4 x + sin4 x = cos 4x.
c) Ta có
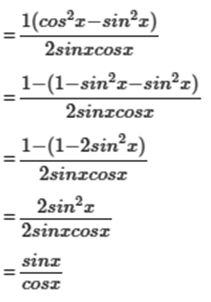
= tan x
Vậy = tanx.
a) Hàm số xác định trên [0; 1) khi m = ?
b) Hàm số xác định trên [3; + ∞) khi m = ?
Lời giải:
a) Điều kiện xác định x ≠ 2m – 1
Để hàm số xác định trên [0; 1)
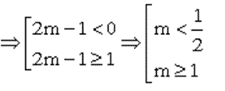
Vậy m < hoặc m ≥ 1 thì hàm số xác định trên [0; 1).
b) Điều kiện xác định x ≠ 2m + 1
Để hàm số xác định trên [3; + ∞)
Thì 2m + 1 < 3
Hay m < 1
Vậy m < 1 thì hàm số xác định trên [3; + ∞).
Câu 51: Tìm m để các phương trình sau có nghiệm duy nhất, vô nghiệm, vô số nghiệm
a) mx – 5 = 2x + m2 – 1
b) mx – 5 = 3x + m2 + 4
Lời giải:
a) mx – 5 = 2x + m2 – 1
⇔ mx – 5 – 2x – m2 + 1 = 0
⇔ x(m – 2) – m2 – 4 = 0
⇔ x(m – 2) = m2 + 4 (*)
+) Với m = 2
(*) ⟺ x . 0 = 22 + 4
⟺ x . 0 = 8
Suy ra phương trình vô nghiệm
+) Với m ≠ 2
(*) ⟺ x =
Suy ra phương trình có nghiệm x =
Vậy phương trình vô nghiệm khi m = 2, phương trình có nghiệm x = khi m ≠ 2.
b) mx – 5 = 3x + m2 + 4
⇔ mx – 5 – 3x – m2 – 4 = 0
⇔ x(m – 3) – m2 – 9 = 0
⇔ x(m – 3) = m2 + 9 (**)
+) Với m = 3
(**) ⟺ x . 0 = 32 + 9
⟺ x . 0 = 18
Suy ra phương trình vô nghiệm
+) Với m ≠ 3
(*) ⟺ x =
Suy ra phương trình có nghiệm x =
Vậy phương trình vô nghiệm khi m = 3, phương trình có nghiệm x = khi m ≠ 3.
Câu 52: Tính tổng: 2 + 4 + 6 + 8 + ... + 100
Lời giải:
Ta có:
2 + 4 + 6 + 8 + ... + 100
= (2 + 100 ) + (4 + 98) + (6 + 96) + ... + (50 + 52)
= 102 + 102 + ... + 102
= 102 x 25
= 2 550
Vậy 2 + 4 + 6 + 8 + ... + 100 = 2 550.
Câu 53: Biện luận m để (1 + m)x2 – 2mx + 2m = 0 có nghiệm.
Lời giải:
Xét phương trình (1 + m)x2 – 2mx + 2m = 0 (*)
Trường hợp 1: m + 1 = 0 Û m = –1.
Khi đó phương trình (*) trở thành: 2x – 2 = 0 Û x = 1.
Do đó khi m = –1 thì phương trình (*) có nghiệm.
Trường hợp 2: m + 1 ≠ 0 Û m ≠ –1.
Khi đó phương trình (*) là phương trình bậc hai một ẩn.
Có: △’ = (–m)2 – 2m(1 + m)
= m2 – 2m – 2m2
= – m2 – 2m
Để phương trình có nghiệm thì Δ' ≥ 0
⟺ – m2 – 2m ≥ 0
⟺ m2 + 2m ≤ 0
⟺ m(m + 2) ≤ 0
⟺ – 2 ≤ m ≤ 0
Kết hợp 2 trường hợp ta có: – 2 ≤ m ≤ 0.
Vậy – 2 ≤ m ≤ 0 thì phương trình đã cho có nghiệm.
Câu 54: Cho phương trình (1 + m)x2 – 2mx + 2m = 0. Tìm m để phương trình:
a) Có nghiệm;
b) Vô nghiệm;
c) Có 2 nghiệm;
d) Có 2 nghiệm phân biệt.
Lời giải:
a) Xét phương trình (1 + m)x2 – 2mx + 2m = 0 (*)
Trường hợp 1: m + 1 = 0 Û m = –1.
Khi đó phương trình (*) trở thành: 2x – 2 = 0 Û x = 1.
Do đó khi m = –1 thì phương trình (*) có nghiệm.
Trường hợp 2: m + 1 ≠ 0 Û m ≠ –1.
Khi đó phương trình (*) là phương trình bậc hai một ẩn.
Có: △’ = (–m)2 – 2m(1 + m)
= m2 – 2m – 2m2
= – m2 – 2m
Để phương trình có nghiệm thì Δ' ≥ 0
⟺ – m2 – 2m ≥ 0
⟺ m2 + 2m ≤ 0
⟺ m(m + 2) ≤ 0
⟺ – 2 ≤ m ≤ 0
Kết hợp 2 trường hợp ta có: – 2 ≤ m ≤ 0.
Vậy – 2 ≤ m ≤ 0 thì phương trình đã cho có nghiệm.
b) Để phương trình vô nghiệm thì Δ' < 0
⟺ – m2 – 2m < 0
⟺ m2 + 2m > 0
⟺ m(m + 2) > 0
⟺
c) Để phương trình có hai nghiệm thì Δ' ≥ 0
⟺ – m2 – 2m ≥ 0
⟺ m2 + 2m ≤ 0
⟺ m(m + 2) ≤ 0
⟺ – 2 ≤ m ≤ 0
Kết hợp điều kiện m ≠ – 1 ta có – 2 ≤ m ≤ 0 và m ≠ – 1.
d) Để phương trình có hai nghiệm phân biệt thì Δ' > 0
⟺ – m2 – 2m > 0
⟺ m2 + 2m < 0
⟺ m(m + 2) < 0
⟺ – 2 < m < 0
Kết hợp điều kiện m ≠ – 1 ta có – 2 < m < 0 và m ≠ – 1.
Tìm mệnh đề đúng trong các mệnh đề sau:
A. Tồn tại giá trị của m để biểu thức không có nghĩa;
B. Hàm số luôn xác định với mọi m;
C. Số nguyên nhỏ nhất để hàm số xác định là m = 1;
D. Tất cả các mệnh đề trên đều sai.
Lời giải:
Đáp án đúng là B
Điều kiện xác định: (2m2 + 1)x2 – 4mx + 2 ≠ 0
Xét tam thức bậc hai f(x) = (2m2+1) x2 – 4mx + 2
Ta có hệ số a = 2m2 + 1 > 0 và
Δ’ = 4m2 – 2(2m2 +1) = – 2 < 0
Suy ra với mọi m ta có f(x) > 0 với mọi x
Vậy tập xác định của hàm số là D = R.
Câu 56: Cho dãy số: 1, 2, 4, 7, 11, 16.... Số thứ 101 là số?
Lời giải:
Ta thấy:
Số thứ nhất : 1
Số thứ hai : 1 + 1 = 2
Số thứ ba: 1 + 1 + 2 = 4
Số thứ tư: 1 + 1 + 2 + 3 = 7
⇒ Số thứ 101: 1 + 1 + 2 + 3 + ...+ 100
Ta có 1 + 1 + 2 + 3 + ...+ 100 = 1 + (1 + 100) + (2 + 99) + ... + (50 + 51)
= 1 + 101 . 50 = 1 + 5 050 = 5 051
Vậy số thứ 101 là 5 051.
Câu 57: Cho dãy số: 1, 2, 4, 7, 11, 16. Hỏi số quy luật của dãy số trên?
Lời giải:
Ta thấy:
1 + 1 = 2
2 + 2 = 4
4 + 3 = 7
7 + 4 = 11
11 + 5 = 16
Vậy quy luật của dãy số là: Cứ số tiếp theo bằng số trước cộng với số thứ tự của số đó trừ 1 trong đó số 1 là số thứ nhất.
Câu 58: Cho a, b, c > 0. Chứng minh rằng:
Lời giải:
Áp dụng bất đẳng thức Cô – si ta có:
![]()
Do đó:
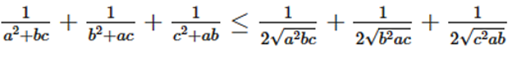
(*)
Áp dụng bất đẳng thức Cô – si ta có:
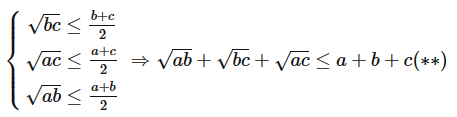
Từ (*) và (**) suy ra
Vậy với a, b, c > 0.
Câu 59: Cho hình vuông ABCD cạnh a, tâm O. Khi đó bằng :
A. a
B. a
C.
D. 2a.
Lời giải:
Đáp án đúng là A
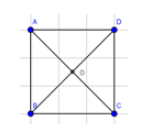
Ta có:
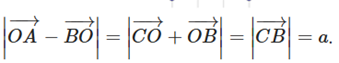
Vậy ta chọn đáp án A.
Lời giải:
Gọi là số tự nhiên cần tìm
+) Xét a1 = 5
Chọn có = 360 cách chọn
Suy ra có 360 số
+) Xét a1 ≠ 5 thì a1 có 5 cách chọn
Đặt chữ số 5 có 4 cách
Chọn 3 vị trí còn lại có
Suy ra có 5 . 4 . = 1 200 số
Vậy có 1 200 + 360 = 1 560 số thỏa mãn yêu cầu đề bài
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.