Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 64)

Ngọc Nguyễn Ngày: 07-08-2023 Tổng hợp kiến thức

376

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 64) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 64)

Câu 1: Một đội công nhân có 40 người được giao nhiệm vụ hoàn thành một công việc trong 15 ngày. Sau khi làm được 3 ngày thì 20 công nhân được điều đi nơi khác. Hỏi đội công nhân đó hoàn thành công việc được giao trong bao nhiêu ngày? Biết rằng năng suất làm việc của mỗi người là như nhau.

Lời giải:

1 ngày cần số người là:

40 × 15 = 600 (người)

3 ngày cần số người là:

40 × 3 = 120 (người)

Đội công nhân đó hoàn thành công việc được giao trong số ngày là:

(600 − 120) : (40 − 20) = 24 (ngày)

Đáp số: 24 ngày.

Câu 2: Một đội công nhân gồm 8 người được giao đắp một đoạn mương trong 20 ngày. Sau khi đắp được 5 ngày, đội đó được bổ sung thêm 16 người về cùng làm. Hỏi đơn vị đó đắp xong đoạn mương được giao trong bao nhiêu ngày? Biết rằng năng suất làm việc của mọi người trong một ngày là như nhau.

Lời giải:

Thời gian để đội công nhân đó làm xong công việc còn lại là:

20 − 5 = 15 (ngày)

Số người của đội đó sau khi được bổ sung thêm là:

8 + 16 = 24 (người)

Thời gian để 1 người làm xong công việc còn lại là:

15 × 8 =120 (ngày)

Thời gian để đội công nhân đó sau khi bổ sung thêm người hoàn thành công việc còn lại là:

120 : 24 = 5 (ngày)

Thời gian để đội công nhân hoàn thành toàn bộ công việc được giao là:

5 + 5 =10 (ngày)

Đáp số: 10 ngày.

Câu 3: Một đội 10 người trong một ngày đào được 35 m nương. Người ta bổ sung thêm 20 người nữa cùng đào thì trong một ngày đào được bao nhiêu mét mương? (Mức đào của mỗi người như nhau).

Lời giải:

Trong một ngày 20 người đào được số mét là:

35 × 20 : 10 = 70 (m)

Trong một ngày cả đội đó đào được số mét là:

35 + 70 = 105 (m)

Đáp số: 105 m mương.

Câu 4: Chứng minh rằng 1 số chính phương có số ước là 1 số lẻ.

Lời giải:

Gọi P là một số chính phương.

Ta có: P = k² ( $k \in ℕ$ )

Giả sử k phân tích ra thừa số nguyên tố là k = ax.by.cz.... (a, b, c là các số nguyên tố)

⇒ P = (ax.by.cz....)²

⇒ P = a²x.b²y.c²z

Vì 2 chia hết cho 2 nên 2x, 2y, 2z, ... cũng chia hết cho 2

⇒ 2x, 2y, 2z, ... là số chẵn

Số lượng ước của P là (2x + 1)(2y + 1)(2z + 1)...

Vì 2x, 2y, 2z, ... là số chẵn nên 2x + 1, 2y + 1, 2z + 1, ... là số lẻ

⇒ (2x + 1)(2y + 1)(2z + 1)... là số lẻ

⇒ Số lượng ước của P là 1 số lẻ

Vậy số chính phương luôn có số ước là 1 số lẻ.

Câu 5: Mẹ bạn hân gửi 100 triệu đồng vào ngân hàng theo hình thức có kì hạn 12 tháng với lãi suất 6% một năm. Hỏi sau một năm mẹ bạn hân nhận được bao nhiêu tiền lãi?

Lời giải:

Sau một năm mẹ bạn Hân nhận tổng cộng số phần trăm là:

100% + 6% = 106%

100 triệu = 100 000 000 đồng

Sau một năm mẹ bạn Hân nhận được số tiền là:

100 000 000 × 106 : 100 = 106 000 000 (đồng)

Số tiền lãi mẹ Hân nhận được số tiền là:

106 000 000 – 100 000 000 = 6 000 000 (đồng)

Đáp số: 6 000 000 đồng.

Câu 6: Mẹ Lan gửi tiết kiệm 100 triệu đồng với lãi suất 0,7% một năm. Sau 1 năm mẹ lan nhận được cả vốn và lãi là bao nhiêu tiền?

Lời giải:

100 triệu = 100 000 000 đồng

Số tiền lãi của mẹ Lan sau 1 năm là:

100 000 000 × 0,7 : 100 = 700 000 (đồng)

Số tiền gốc và lãi của mẹ Lan là:

100 000 000 + 700 000 = 100 700 000 (đồng)

Đáp số: 100 700 000 đồng

Câu 7: Cho tập hợp A = 0; 1; 2; 3; 4; 5; 6; 7. Hỏi từ tập A có thể lập được bao nhiêu chữ số tự nhiên gồm 5 chữ số đôi một khác nhau sao cho một trong 3 chữ số đầu tiên phải bằng 1?

Lời giải:

Gọi số đó là a b c d e

Trường hợp 1: a = 1

+ b có 7 cách chọn.

+ c có 6 cách chọn.

+ d có 5 cách chọn.

+ e có 4 cách chọn.

Nên có: 7.6.5.4 = 840 số

Trường hợp 2:b = 1

+ a ≠ b , a ≠ 0 nên có 6 cách chọn.

+ c có 6 cách chọn.

+ d có 5 cách chọn.

+ e có 4 cách chọn.

Nên có: 6.6.5.4 = 720 số

Trường hợp 3: c = 1.

+ a ≠ c , a ≠ 0 nên có 6 cách chọn.

+ b có 6 cách chọn.

+ d có 5 cách chọn.

+ e có 4 cách chọn.

Nên có 6.6.5.4=720 số

Có tất cả số số là: 840 + 720 + 720 = 2280 (số)

Vậy có 2280 số.

Câu 8: Một xe chạy trọng 2,5 giờ. 1 giờ đầu xe chạy với tốc độ trung bình 60 km/h, 1,5 giờ sau xe chạy với tốc trung bình 40 km/h. Tính tốc độ trung bình của xe trông suốt thời gian chuyển động?

Lời giải:

Tốc độ trung bình của xe trong toàn bộ khoảng thời gian chuyển động là:

$v_{t b} = \frac{s_{1} + s_{2}}{t_{1} + t_{2}} = \frac{v_{1} t_{1} + v_{2} t_{2}}{t_{1} + t_{2}} = \frac{1.60 + 1,5.40}{2,5} = 48$ (km/h)

Đáp số: 48 km/h.

Câu 9: Một xe chạy trong 5 giờ: 2 giờ đầu xe chạy với tốc độ trung bình 60 km/h; 3 giờ sau xe chạy với tốc độ trung bình 40 km/h. Tốc độ trung bình của xe trong suốt thời gian chuyển động là:

A. 48 km/h;

B. 50 km/h;

C. 35 km/h;

D. 45 km/h.

Lời giải:

Đáp án đúng là: A

Quãng đường xe đi được trong 2 giờ đầu là: s₁= 60.2 = 120 (km)

Quãng đường xe đi được trong 3 giờ sau là: s₂ = 40.3 = 120 (km)

Tốc độ trung bình của xe là: v = 240 : 5 = 48 (km/h)

Đáp số: 48 km/h.

Câu 10: Mệnh đề nào sau đây đúng?

A. cos2a = cos²a – sin²a;

B. cos2a = cos²a + sin²a;

C. cos2a = 2cos²a + 1;

D. cos2a = 2sin²a – 1.

Lời giải:

Đáp án đúng là A.

Ta có: cos2a = cos²a – sin²a = 2cos²a – 1 = 1 – 2sin²a.

Câu 11: Có bao nhiêu số tự nhiên có 3 chữ số phân biệt mà tổng các chữ số là số lẻ.

Lời giải:

Gọi số tự nhiên có 3 chữ số phân biệt là $\bar{a b c}$

Tổng các chữ số là số lẻ có các trường hợp sau:

TH1: Số tự nhiên có 3 chữ số phân biệt đều là số lẻ

Chọn a, b, c lần lượt có số cách là 5, 4, 3 cách

⇒ có 5.4.3 = 60 cách

TH2: Số tự nhiên có 3 chữ số phân biệt trong đó có 2 chữ số chẵn và 1 chữ số lẻ

Nếu a lẻ thì a có 5 cách chọn

b, c lần lượt có 5, 4 cách chọn

Nếu chữ số lẻ ở hàng chục và hàng đơn vị thì

a có 4 cách chọn

Chữ số chẵn còn lại có 4 cách chọn

Chữ số lẻ có 5 cách chọn

⇒ có 5.5.4 + 2.4.4.5 = 260 cách

Vậy số số tự nhiên có 3 chữ số phân biệt tổng các chữ số là số lẻ là:

60 + 260 = 320 số.

Đáp số: 320 số.

Câu 12: Lớp 5A có 35 học sinh, trong đó có 14 em đăng kí tham gia các câu lạc bộ ngoại khoá do nhà trường tổ chức. Hỏi số học sinh lớp 5A đăng kí tham gia các câu lạc bộ chiếm bao nhiêu phần trăm số học sinh của lớp 5A?

Lời giải:

Số học sinh lớp 5A đăng kí tham gia các Câu lạc bộ chiếm số phần trăm số học sinh của lớp 5A là:

$\frac{14}{35} .100 % = 40 %$

Đáp số: 40%

Câu 13: Cho ∆DMN cân tại D có DM = DN = 6 cm, MN = 5 cm. Phân giác của góc M cắt DN tại I, phân giác góc N cắt DM tại K. Tính tỉ số KM và KD.

Lời giải:

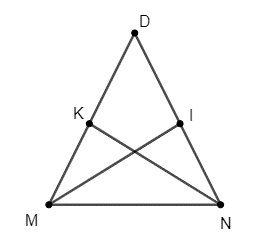
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 64) (ảnh 1)

Theo tính chất của đường phân giác trong tam giác ta có:

$\frac{D K}{M K} = \frac{D N}{M N} = \frac{6}{5}$

Câu 14: Giả sử độ cao h (đơn vị: mét) của một quả bóng golf tính theo thời gian t (đơn vị: giây) trong một lần đánh của vận động viên được xác định bằng một hàm số bậc hai và giá trị tương ứng tại một số thời điểm được cho bởi bảng dưới đây:

Thời gian (s)	0	0,5	1	2	3
Độ cao (m)	0	28	48	64	48

a) Xác định hàm số bậc hai biểu thị độ cao h(m) của quả bóng gofl tính theo thời gian t(s).

b) Sau bao lâu kể từ khi vận động viên đánh bóng thì bóng lại chạm đất?

Lời giải:

a) Xét hàm số bậc hai biểu thị độ cao h phụ thuộc thời gian t có dạng

h(t) = at² + bt + c, trong đó a ≠ 0. Theo đề bài:

Với t = 0, h = 0, ta có: c = 0 nên h(t) = at² + bt. Khi đó:

+ Với t = 1, h = 48, ta có: a . 1² + b . 1 = 48 ⇔ a + b = 48.

+ Với t = 2, h = 64, ta có: a . 2² + b . 2 = 64 ⇔ 4a + 2b = 64.

Giải hệ phương trình:

$\{\begin{cases} a + b = 48 \\ 4 a + 2 b = 64 \end{cases} \Leftrightarrow \{\begin{cases} a = - 16 \\ b = 64 \end{cases}$

Suy ra h(t) = –16t² + 64t.

Thay các giá trị tương ứng còn lại của bảng vào công thức trên, ta thấy phù hợp.

Vậy hàm số bậc hai cần tìm là h(t) = –16t² + 64t.

b) Bóng chạm đất khi h(t) = 0 ⇔ – 16t² + 64t = 0.

Suy ra t = 0 hoặc t = 4.

Vậy sau 4 giây kể từ khi vận động viên đánh bóng thì bóng lại chạm đất.

Câu 15: Cho hình chữ nhật ABCD có AB = 12 cm, BC = 9 cm. Bán kính R của đường tròn đi qua bốn đỉnh của hình chữ nhật là

A. R = 15 cm;

B. R = 12, 5 cm;

C. R = 7,5 cm;

D. R = 7 cm.

Lời giải:

Đáp án đúng là: C

Ta có đường kính của đường tròn chính là đường chéo của hình chữ nhật.

Nên suy ra: $R = \frac{\sqrt{12^{2} + 9^{2}}}{2} = 7,5$ (cm)

Đáp số: 7,5 cm.

Câu 16: Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm. Tính khoảng các từ tâm O đến dây AB.

Lời giải:

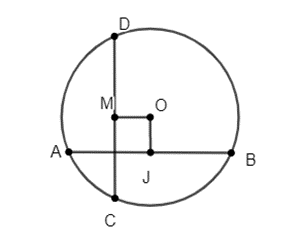
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 64) (ảnh 2)

Kẻ OJ vuông góc với AB tại J.

Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.

Ta được $A J = \frac{1}{2} A B = 4$ (cm)

Áp dụng định lí Pitago trong tam giác vuông OAJ có:

OJ² = OA² – AJ² = 5² – 4² = 9 (OA = R = 5cm)

Do đó OJ = 3 (cm)

Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.

Câu 17: Tìm giá trị lớn nhất của hàm số: y = 3x² + x – 1 trên đoạn [−1; 1].

Lời giải:

y’ = 6x + 1

⇒ y’ = 0

$\Leftrightarrow x = \frac{- 1}{6}$

y(−1) = 1; y(1) = 3; $y (- \frac{1}{6}) = - 1$

⇒ Min = −1

Câu 18: Anh An là nhân viên bán hàng tại siêu thị điện máy. Anh An kiếm được một khoản hoa hồng 600 nghìn đồng cho mỗi máy giặt và 1,3 triệu dồng cho mỗi tủ lạnh mà anh ấy bán được. Hỏi để nhận được từ 10 triệu đồng trở lên tiền hoa hồng thì anh An cần bán bao nhiêu máy giặt và tủ lạnh.

Lời giải:

Gọi x và y lần lượt là số máy giặt và tủ lạnh anh bán được (x ; y ∈ ℕ)

Số tiền thu được: 0,6x + 1,3y (triệu đồng)

Theo bài ra, ta có bất phương trình:

0,6x + 1,3y ≥ 10 ⇔ 0,6x + 1,3y – 10 ≥ 0

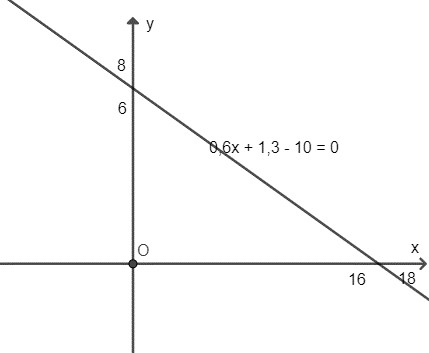
Vẽ đường thẳng (d): 0,6x + 1,3y – 10 = 0 trên mặt phẳng toạ độ Oxy

Thấy điểm O(0; 0) không thuộc BPT (1) nên miền nghiệm BPT là phần mặt phẳng không chứa O, kể cả đường thẳng (d).

Vậy để nhận được từ 10 triệu đồng trở lên tiền hoa hồng thì anh An cần bán x máy giặt và y tủ lạnh sao cho (x, y) là điểm thuộc phần mặt phẳng không chứa điểm O, kể cả đường thẳng (d).

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 64) (ảnh 3)

Câu 19: Nhà trường tổ chức cho học sinh khối 5 đi thăm quan. Nễu xếp 40 học sinh một xe thì cần 14 xe ô tô. Hỏi nếu xếp 35 học sinh thì cần bao nhiêu xe? (sức chở của mỗi xe là như nhau)

Lời giải:

Số học sinh đi tham quan là:

40 x 14 = 560 ( học sinh)

Nếu mỗi xe chở 35 học sinh thì cần số xe là:

560 : 35 = 16 (xe)

Đáp số: 16 xe

Câu 20: Tính a² + b² biết a + b = 5 và ab = 1.

Lời giải:

Ta có:

a² + b²

= (a + b)² − 2ab

= 5² – 2.1 = 25 – 2 = 23

Vậy a² + b² = 23 khi a + b = 5 và ab = 1.

Câu 21: Cho 2.(a² + b²) = (a + b)². Chứng minh rằng a = b.

Lời giải:

(a²+ b²) = (a + b)²

⇔ 2a²+ 2b² = a² + b² + 2ab

⇔ 2a² – a² + 2b² – b² – 2ab = 0

⇔ a² + b² – 2ab = 0

⇔ a² – 2ab + b² = 0

⇔ (a – b)² = 0

⇔ a – b = 0

⇔ a = b (đpcm)

Câu 22: Một công ty điện tử sản xuất hai kiểu radio trên hai dây chuyền độc lập. Radio kiểu một sản xuất trên dây chuyền một với công suất 45 radio/ngày radio kiểu hai sản xuất trên dây chuyền 2 với công suất 80 radio/ngày. Để sản xuất một chiếc radio kiểu một cần 12 linh kiện, để sản xuất một chiếc radio kiểu 2 cần 9 linh kiện tiền lãi khi bán một chiếc radio kiểu một là 250 000 đồng tiền lãi thu được khi bán một chiếc Rario kiểu 2 là 180 000 đồng. Hỏi cần sản xuất như thế nào để tiền lãi thu được là nhiều nhất biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 900.

Lời giải:

Gọi số radio kiểu một và kiểu hai mà công ty này sản xuất trong một ngày lần lượt là x, y (x, y ∈ N*,chiếc)

Số tiền lãi công ty thu được trong 1 ngày:

f(x, y) = 250x + 180y (nghìn đồng)

Công suất của dây chuyền 1 là 45 radio/ngày và dây chuyền 2 là 80 radio/ngày

$\Rightarrow \{\begin{cases} 0 \leq x \leq 45 \\ 0 \leq y \leq 80 \end{cases}$

Để sản xuất 1 chiếc radio kiểu một cần 12 linh kiện điện tử A và một chiếc radio kiểu hai cần 9 linh kiện này. Số linh kiện này được cung cấp mỗi ngày không quá 900

⇒ 12x + 9y ≤ 900

Ta có hệ bất phương trình: $\{\begin{cases} 0 \leq x \leq 45 \\ 0 \leq y \leq 80 \\ 12 x + 9 y \leq 900 \end{cases}$

Miền của hệ BPT là phần mặt phẳng đậm nhất trong hình, kể cả biên

Khi đó f(x, y) đạt GTLN khi (x, y) là một trong số các điểm A(45; 0); B(45; 40); C(15; 80); D(0; 80).

Thay vào hàm f(x, y) ta có f(x, y) đạt GTLN bằng 18 450 000 đồng khi (x, y) = (45, 40).

Câu 23: Hình đa giác lồi 6 cạnh có bao nhiêu đường chéo?

A. 6;

B. 7;

C. 8;

D. 9.

Lời giải:

Đáp án đúng là: D.

Số đường chéo của đa giác lồi n đỉnh là: $\frac{x (x - 3)}{2}$ .

Áp dụng công thức ta có số đường chéo của hình lục giác lồi là: $\frac{6. (6 - 3)}{2} = 9$ .

Câu 24: Trung bình mỗi con gà ăn hết 102 g thức ăn trong một ngày. Hỏi trại nuôi gà đó cần bao nhiêu ki-lô-gam thức ăn cho 350 con gà trong 30 ngày?

Lời giải:

1 ngày trang trại cần số thức ăn là:

102 x 350 = 35700 (g) = 35,7 (kg)

Trại nuôi gà đó cần số ki-lô-gam thức ăn cho 350 con gà trong 30 ngày là:

35,7 x 30 = 1071 (kg)

Đáp số: 1071 kg.

Câu 25: Từ các số 0; 1; 2; 7; 8; 9 tạo được bao nhiêu số lẻ có 5 chữ số khác nhau?

Lời giải:

Gọi $\bar{a b c d e}$ là số cần tìm.

Chọn e có 3 cách.

Chọn a ≠ 0 và a ≠ e có 4 cách.

Chọn 3 trong 4 số còn lại sắp vào b, c, d có cách.

Vậy có $3.4. A_{4}^{3} = 288$ số.

Đáp số: 288 số.

Câu 26: Có tất cả bao nhiêu số tự nhiên chẵn gồm 5 chữ số khác nhau được thành lập từ các chữ số 1, 2, 3, 4, 5?

Lời giải:

Gọi số cần tìm có dạng $\bar{a b c d e}$ .

Vì là số tự nhiên chắn nên e ∈ {2; 4}

Khi đó a có 4 cách chọn

b có 3 cách chọn

c có 2 cách chọn

d có 1 cách chọn

Vậy số số cần tìm là: 2.4.3.2.1 = 48 (số)

Câu 27: Một mảnh vườn hình vuông cạnh 20 m. Người ta làm một lối đi xung quanh vườn rộng 2 m thuộc đất của vườn. Phần đất còn lại dùng để trồng trọt. Tính diện tích trồng trọt của mảnh vườn.

Lời giải:

Phần còn lại để trồng trọt là hình vuông có cạnh: 20 − 2 − 2 = 16 (m)

Diện tích trồng trọt của mảnh vườn là: 16 . 16 = 256 (m²)

Vậy diện tích trồng trọt của mảnh vườn là 256 m².

Câu 28: Rô bốt có hai cái cốc loại 250 ml và 400 ml. Chỉ dùng hai cái cốc đó, làm thế nào để rô bốt lấy được 100 ml nước từ chậu nước.

Lời giải:

Ta có: 250 x 2 – 400 = 100

Vậy đổ 2 cốc 250 ml nước vào cốc 400 ml thì còn dư lại 100 ml trong cốc 250 ml.

Câu 29: Cho hàm số (P): y = x² – 3x + 2 và (d): y = x + m. Tìm M để (d) và (P) cắt nhau tại hai điểm phân biệt.

Lời giải:

Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình:

x² – 3x + 2 = x + m

⇔ x² – 4x + 2 – m = 0

Ta có: ∆’ = (–2)² – (2 – m) = m + 2

Để d) và (P) cắt nhau tại hai điểm phân biệt thì ∆’ > 0

$\Leftrightarrow m + 2 > 0 \Leftrightarrow m > - 2$

Vậy m > –2 thì (d) và (P) cắt nhau tại hai điểm phân biệt.

Câu 30: Cho hàm số y = (2m – 1)x + 3 – m có đồ thị (d). Xác định m để đường thẳng (d) song song với đồ thị hàm số y = 2x + 5.

Lời giải:

Để đường thẳng (d) song song với đường thẳng y = 2x + 5 thì

$\{\begin{cases} 2 m - 1 = 2 \\ 3 - m \neq 5 \end{cases} \Leftrightarrow \{\begin{cases} m = \frac{3}{2} \\ m \neq - 2 \end{cases} \Leftrightarrow m = \frac{3}{2}$

Vậy $m = \frac{3}{2}$ .

Câu 31: Cho hai tập khác rỗng A = (m – 1; 4] và B = (–2; 2m + 2), m ∈ ℝ. Tìm m để A ∩ B ≠ ∅.

A. –2 < m < 5

B. m > –3

C. –1 < m < 5

D. 1 < m < 5.

Lời giải:

Đáp án đúng là: A

Do A và B khác rỗng nên $\{\begin{array}{l} m - 1 < 4 \\ 2 m + 2 > - 2 \end{array} \Leftrightarrow \{\begin{cases} m < 5 \\ m > - 2 \end{cases}$

⇔ –2 < m < 5

Để A ∩ B = ∅

$\Leftrightarrow 2 m + 2 \leq m - 1 \Leftrightarrow m \leq - 3$

Mà –2 < m < 5 nên m ∈ ∅

Do đó không có giá trị nào của m để A ∩ B = ∅

Suy ra với mọi m ∈ (–2; 5) thì A ∩ B ≠ ∅

Vậy ta chọn đáp án A.

Câu 32: Hãy chọn câu đúng. Trục đối xứng của hình thang cân là:

A. Đường thẳng đi qua trung điểm hai cạnh bên của hình thang cân.

B. Đường chéo của hình thang cân.

C. Đường thẳng vuông góc với hai đáy của hình thang cân.

D. Đường thẳng đi qua trung điểm hai đáy của hình thang cân.

Lời giải:

Đáp án đúng là: D

Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.

Vậy ta chọn đáp án D.

Câu 33: Đường tròn có 1 tâm đối xứng và 1 trục đối xứng, đúng hay sai?

Lời giải:

Khẳng định trên là sai vì:

Đường tròn có 1 tâm đối xứng và vô số trục đối xứng (mỗi đường kính là một trục đối xứng).

Câu 34: Cho 4 điểm A(1; –2), B(0; 3), C(–3; 4), D(–1; 8). Ba điểm nào trong 4 điểm đã cho là thẳng hàng?

A. A, B, C;

B. B, C, D;

C. A, B, D;

D. A, C, D.

Lời giải:

Đáp án đúng là: C

Ta có:

$\vec{A D} (- 2; 10), \vec{A B} (- 1; 5) \Rightarrow \vec{A D} = 2 \vec{A B}$

Suy ra 3 điểm A, B, D thẳng hàng

Vậy ta chọn đáp án C.

Câu 35: Tính nhanh [(–59) + 71] – [(–83) – (–95)].

Lời giải:

Ta có:

[(–59) + 71] – [(–83) – (–95)]

= (–59) + 71 + 83 + (–95)

= 12 + (–12)

= 0.

Câu 36: Phương là gì, chiều là gì, hướng là gì trong toán học?

Lời giải:

Hai vectơ gọi là cùng phương khi giá của chúng song song hoặc trùng nhau.

Hai vectơ cùng hướng (hoặc chiều) khi chúng là vectơ cùng phương và cùng xác định 1 hướng.

Câu 37: Tìm số a để đa thức 2x³ – 3x² + x + a chia hết cho đa thức x + 2.

Lời giải:

Ta có:

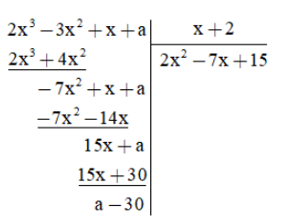
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 64) (ảnh 4)

Để đa thức 2x³ – 3x² + x + a chia hết cho đa thức x + 2 thì số dư a – 30 = 0

Hay a = 30.

Vậy a = 30 thì đa thức 2x³ – 3x² + x + a chia hết cho đa thức x + 2.

Câu 38: Tìm hệ số x⁵ trong khai triển đa thức của x(1 – 2x)⁵ + x²(1 + 3x)¹⁰.

A. 3310

B. 2130

C. 3210

D. 3320.

Lời giải:

Đáp án đúng là D

Đặt f(x) = x(1 – 2x)⁵ + x²(1 + 3x)¹⁰

Ta có:

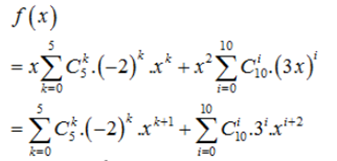
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 64) (ảnh 5)

Vậy hệ số của x⁵ trong khai triển ứng với k = 4 và i = 3 là:

$C_{5}^{4} . (- 2) {}_{4}+ C_{10}^{3} {.3}^{3} = 3320$ .

Câu 39: Tính chu vi của hình chữ nhật có các cạnh là x = 3,456 ± 0,01 (m) và y = 12,732 ± 0,015 (m) và ước lượng sai số tuyệt đối mắc phải.

A. L = 32,376 ± 0,025 và ∆L ≤ 0,05

B. L = 32,376 ± 0,05 và ∆L ≤ 0,025

C. L = 32,376 ± 0,5 và ∆L ≤ 0,5

D. L = 32,376 ± 0,05 và ∆L ≤ 0,05.

Lời giải:

Đáp án đúng là D

Chu vi hình chữ nhật là:

$L = 2 (x + y) = 2 (3,456 + 12,732) = 32,376 (m)$

Sai số tuyệt đối là:

$Δ_{L} \leq 2 (0,01 + 0,015) = 0,05$

Vậy ta chọn đáp án D.

Câu 40: Tính giá trị của biểu thức:

a) x³ + 12x² + 48x + 64 tại x = 6

b) x^3 – 6x^2 + 12x – 8 tại x = 22

Lời giải:

a) Ta có x³ + 12x² + 48x + 64

= x³ + 3 . x² . 4 + 3 . x . 4² + 4³

= (x + 4)³

Tại x = 6, giá trị biểu thức bằng

(6 + 4)³ = 10³ = 1 000.

b) Ta có x³ – 6x² + 12x – 8

= x³ – 3 . x² . 2 + 3 . x . 2² – 2³

= (x – 2)³

Tại x = 22, giá trị biểu thức bằng

(22 – 2)³ = 20³ = 8 000.

Câu 41: Cho parabol (P): y = x² + x + 2 và đường thẳng (d): y = ax + 1. Tìm tất cả các giá trị thực của tham số a để (P) tiếp xúc với (d).

A. a = –1, a = 3

B. a = 2

C. a = 1, a = –3

D. Không tồn tại giá trị của a.

Lời giải:

Đáp án dúng là A

Xét phương trình hoành độ giao điểm: x² + x + 2 = ax + 1

⇔ x² + (1 – a) x + 1 = 0

Để (P) tiếp xúc với (d) thì phương trình có nghiệm kép hay

$Δ = {(1 - a)}^{2} - 4 = 0 \Leftrightarrow a = - 1$ hoặc a = 3

Vậy ta chọn đáp án A.

Câu 42: Tìm số nguyên x:

a) 46 – x = –21 + (–87)

b) x – 96 = (443 – x) – 15

c) (–x + 281 +534) = 499 + (x – 48)

d) –(754 + x) = (x – 12 – 741) – 23.

Lời giải:

a) 46 – x = –21 + (–87)

⇔ 46 – x = –108

⇔ x = 46 – (–108)

⇔ x = 154

Vậy x = 154.

b) x – 96 = (443 – x) – 15

⇔ x – 96 = 443 – x – 15

⇔ x – 96 = 428 – x

⇔ x + x = 428 + 96

⇔ 2x = 524

⇔ x = 262

Vậy x = 262.

c) (–x + 281 +534) = 499 + (x – 48)

⇔ –x + 281 +534 = 499 + x – 48

⇔ –x + 815 = 451 + x

⇔ 815 – 451 = x + x

⇔ 364 = 2x

⇔ 182 = x

Vậy x = 182.

d) –(754 + x) = (x – 12 – 741) – 23

⇔ –754 – x = x – 12 – 741 – 23

⇔ –754 – x = x – 776

⇔ –754 + 776 = x + x

⇔ 22 = 2x

⇔ 11 = x

Vậy x = 11.

Câu 43: Tìm số a; b biết a + b = 30 và [a; b] = 6(a; b).

Lời giải:

Gọi (a, b) = d

Suy ra a = dm, b = dn, trong đó m, n, d ∈ N*

(m, n) = 1

Giả sử a > b nên m > n

Ta có:

a . b = (a, b) . [a, b]

⇔ dm . dn = d . 6 . d

⇔ mn = 6

Theo đề bài ta có a + b = 30

Suy ra dm + dn = 30

Hay m + n = 30

Vì m, n, d ∈ ℕ*, m > n nên ta có bảng sau:

m	n	d	a	b
6	1	$\frac{30}{7}$ (loại)
3	2	6	18	12

Vậy (a, b) = (18, 12).

Câu 44: Biết số gần đúng là a = 37 975 421 có độ xác định d = 150. Hãy ước lượng sai số tương đối của a.

A. δ ≤ 0,0000099

B. δ ≤ 0,000039

C. δ ≤ 0,0000039

D. δ < 0,000039.

Lời giải:

Đáp án đúng là: C

Các số đáng tin của a là 3, 7, 9, 7, 5

Suy ra cách viết chuẩn của a = 37 975 . 10³

Sai số tương đối thỏa mãn $δ_{a} \leq \frac{150}{37975421} = 0,0000039$

Vậy ta chọn đáp án C.

Từ khóa :

Giải bài tập

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

295

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

315

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

343

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

290