Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 27) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 27)

Câu 1: Cho x ∈ ℕ. Hãy chứng minh x2+1 không chia hết cho 4.

Lời giải:

Giả sử như mệnh đề trên đúng: $n^2+1$  chia hết cho 4

* Nếu n chẵn: n = 2k, k ∈ N

$\Rightarrow n^2+1=4k^2+1$ không chia hết cho 4.

* Nếu n lẻ: n = 2k + 1

$\Rightarrow n^2+1=4k^2+4k+2\Rightarrow n^2+1=4k\left(k+1\right)+2$ không chia hết cho 4.

k, k + 1 là 2 số tự nhiên liên tiếp.

Câu 2: Cho n ∈ ℕ, chứng minh rằng n2+n+1  không chia hết cho 4 và không chia hết cho 5.

Lời giải:

n2+n+1=n(n+1)+1 mà n(n+1)⋮2 .

Nên n(n + 1) + 1 lẻ nên không chia hết cho 4

Ta chứng minh: n2+n  không chia 5 dư 4; n chia 5 dư 0 thì đúng; 1 cũng đúng;...

Nên n2+n+1  không chia 5 dư 4 + 1 = 5 hay 0 nên có đpcm.

Câu 3: Cho phương trình cotx=√3 . Tính các nghiệm của phương trình ?

Lời giải:

Ta có: cotx=√3=cotπ6

⇔x=π6+kπ(k∈ℤ).

Câu 4: Giá trị của M=cos215+cos225+cos235+cos245+cos2105+cos2115+cos2125 là ?

Lời giải:

$$\begin{gathered} M={\cos }^{2}15+{\cos }^{2}25+{\cos }^{2}35+{\cos }^{2}45+{\cos }^{2}105+{\cos }^{2}115+{\cos }^{2}125 \\ ={\cos }^{2}15+{\cos }^{2}25+{\cos }^{2}35+{\cos }^{2}45+{\sin }^{2}15+{\sin }^2+{\sin }^{2}25+{\sin }^{2}35 \\ =\left({\cos }^{2}15+{\sin }^{2}15\right)\left({\sin }^{2}25+{\cos }^{2}25\right)+\left({\cos }^{2}35+{\sin }^{2}35\right)+{\cos }^{2}45 \end{gathered}$$

= 1 + 1 + 1 + $\frac{1}{2}=\frac{7}{2}$ .

Câu 5: Một đơn vị bộ đội chuẩn bị 768 kg lương thực đủ cho 80 người ăn trong 12 ngày luyện tập. Trước ngày tập trung quân ban chỉ huy báo về là số người sẽ tăng gấp 3 số dự kiến. Vậy để đủ ăn trong số ngày luyện tập như dự kiến đơn vị đó phải mua thêm số lương thực là ?

Lời giải:

Mỗi người ăn hết số kg lương thực trong 12 ngày là: 768 : 12 = 64 (kg)

Số người sau khi tăng lên gấp 3 của đơn vị là: 12 x 3 = 36 (người)

Số lương thực cần cho 36 người là: 36 x 64 = 2304 (kg)

Số lương thực cần mua thêm là: 2304 – 768 = 1536 (kg).

Câu 6: ∆ABC có ˆA=120° . Khẳng định nào sau đây đúng ?

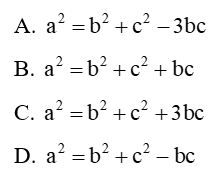
Lời giải:

Đáp án đúng là: B

Áp dụng định lí côsin tại đỉnh A ta có: a2=b2+c2−2bc.cosA

⇒a2=b2+c2−2bc.cos120°=b2+c2+bc.

Câu 7: Trên các cạnh AB, BC, CA của ∆ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n + 6 điểm đã cho là 247.

Lời giải:

Nhận xét: Mỗi tam giác được lập thành do một cách chọn 3 điểm sao cho 3 điểm đó không thẳng hàng tức là không cùng nằm trên một cạnh của ∆ABC.

Chọn ngẫu nhiên 3 điểm từ n + 6 điểm đã cho có: C3n+6  cách.

Chọn 3 điểm chỉ nằm trên đúng 1 cạnh của ∆ABC có: C34+C3n  (cách).

Số tam giác lập thành là: C3n+6−(C34+C3n)=247

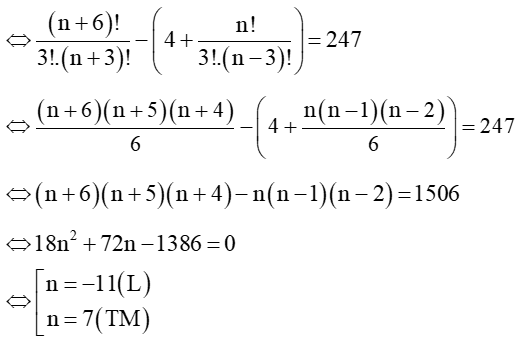
Vậy n = 7.

Câu 8: Tính GTLN của diện tích 1 tam giác biết 3 trong 2 cạnh của nó là 5 và 8.

Lời giải:

Giả sử AB = 5, AC = 8. Xét trường hợp $\widehat{BAC}$  nhọn:

Áp dụng công thức sau: $S_{ABC}=\frac{1}{2}AB.AC.\sin \widehat{BAC}$  với $\widehat{BAC}$  nhọn.

Do $\sin \widehat{BAC}<1$ nên $S_{ABC}<\frac{AB.AC}{2}$

Xét trường hợp $\widehat{BAC}$ tù. Có công thức sau đây: $S_{ABC}=\frac{1}{2}AB.AC.\sin \left(180°-\widehat{BAC}\right)$

Lập luận tương tự vẫn có $S_{ABC}<\frac{AB.AC}{2}$

Trường hợp $\widehat{BAC}$  vuông ta có $S_{ABC}=\frac{AB.AC}{2}$

Vậy GTLN của $S_{ABC}$  là $\frac{AB.AC}{2}=20.$

Câu 9: Tìm m để phương trình 3sinx – 4cosx = 2m có nghiệm ?

Lời giải:

3sinx – 4cosx = 2m

Để phương trình có nghiệm: $a^2+b^2\ge c^2$

$$\begin{gathered} \iff 3^2+4^2\ge {\left(2m\right)}^2\iff 9+16\ge 4m^2 \\ \iff 25\ge 4m^2\iff m^2\le \frac{25}{4} \\ \iff -\frac{5}{2}\le m\le \frac{5}{2} \end{gathered}$$

Vậy với m ∈ $\left[-\frac{5}{2};\frac{5}{2}\right]$  thì phương trình có nghiệm.

Câu 10: Giải phương trình: $x^2-2x=0$ .

Lời giải:

$$\begin{gathered} x^2-2x=0 \\ \iff x\left(x-2\right)=0 \\ \iff \left[\begin{array}{c}x=0\\ x-2=0\end{array}\right. \\ \iff \left[\begin{array}{c}x=0\\ x=2\end{array}\right. \end{gathered}$$

Câu 11: Tìm x biết: $x^3-4x=0$ .

Lời giải:

$$\begin{gathered} x^3-4x=0 \\ \iff x\left(x^2-4\right)=0 \\ \iff x\left(x-2\right)\left(x+2\right)=0 \\ \iff \left[\begin{array}{c}x=0\\ x=2\\ x=-2\end{array}\right. \end{gathered}$$

Câu 12: Xác định a để đa thức 10x2−7x+a chia hết cho 2x – 3.

Lời giải:

(10x2−7x+a)⋮(2x−3)

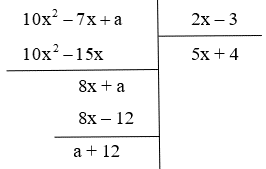
Để 10x2−7x+a  chia hết cho 2x – 3 thì a + 12 = 0 ⟺ a = – 12.

Câu 13: Xếp 5 người A, B, C, D, E ngẫu nhiên vào 1 chiếc ghế có 5 chỗ ngồi. Tính xác suất để C ngồi chính giữa.

Lời giải:

Có 1 cách xếp C chính giữa

4 người còn lại hoán vị có 4! Cách xếp.

Xác suất C ngồi giữa: 4!5!=15 .

Câu 14: Xếp ngẫu nhiên 5 học sinh A, B, C, D, E ngồi vào 1 dãy 5 ghế thẳng hàng (mỗi bạn ngồi 1 ghế). Tính xác suất để 2 bạn A và B không ngồi cạnh nhau.

Lời giải:

Xếp 5 học sinh A, B, C, D, E vào 1 dãy 5 ghế thẳng hàng có 5! cách xếp ⇒ n(Ω) = 5! =120.

Gọi X là biến cố: “2 bạn A và B không ngồi cạnh nhau” ⇒ Biến cố đối ˉX : “ 2 bạn A và B ngồi cạnh nhau”

Buộc 2 bạn A và B coi là 1 phần tử, có 2! Cách đổi chỗ 2 bạn A và B trong buộc này.

Bài toán trở thành xếp 4 bạn (AB), C, D, E vào dãy 4 ghế thẳng hàng ⇒ Có 4! cách xếp.

⇒n(ˉX)=2!.4!=48⇒P(ˉX)=n(ˉX)n(Ω)=48120=25⇒n(¯¯¯X)=2!.4!=48⇒P(¯¯¯X)=n(¯¯¯X)n(Ω)=48120=25

Vậy P(X) = 1 – P(ˉX)=1−25=35 .

Câu 15: Tính đạo hàm của hàm số y=(x2+2x)e−x ?

Lời giải:

y=(x2+2x)e−xy'=(x2+2x)'.e−x+(x2+2x).(e−x)'=(2x+2).e−x+(x2+2x).(−e−x)=(2x+2).e−x−(x2+2x).e−x=e−x(2x+2−x2−2x)=(−x2+2).e−xy=(x2+2x)e−xy′=(x2+2x)′.e−x+(x2+2x).(e−x)′=(2x+2).e−x+(x2+2x).(−e−x)=(2x+2).e−x−(x2+2x).e−x=e−x(2x+2−x2−2x)=(−x2+2).e−x

Câu 16: Chứng minh biểu thức sau lớn hơn 0 ∀x : A=x2+6x−11 .

Lời giải:

A=x2+6x−11A=(x2+2.3x+9)−9−11A=(x+3)2−20>0∀xA=x2+6x−11A=(x2+2.3x+9)−9−11A=(x+3)2−20>0∀x

Câu 17: Tìm nghiệm của phương trình $\sqrt{3}\cos x+\mathrm{s}\text{inx}=-2$ ?

Lời giải:

$$\begin{gathered} PT\iff \frac{\sqrt{3}}{2}\cos x+\frac{1}{2}\sin x=-1 \\ \iff \sin \left(x+\frac{\pi }{3}\right)=-1 \\ \iff x+\frac{\pi }{3}=-\frac{\pi }{2}+k2\pi \\ \iff x=-\frac{5\pi }{6}+k2\pi ,k\in \mathbb{Z} \end{gathered}$$

PT⇔√32cosx+12sinx=−1⇔sin(x+π3)=−1⇔x+π3=−π2+k2π⇔x=−5π6+k2π,k∈Z

Câu 18: Rút gọn biểu thức a2+√aa−√a+1−2a+√a√a+1 .

Lời giải:

A = $\frac{a^2+\sqrt{a}}{a-\sqrt{a}+1}-\frac{2a+\sqrt{a}}{\sqrt{a}}+1$ . ĐK: a > 0

$$\begin{gathered} A=\frac{\sqrt{a}\left(\sqrt{a^3}+1\right)}{a-\sqrt{a}+1}-\frac{\sqrt{a}\left(2\sqrt{a}+1\right)}{\sqrt{a}}+1 \\ A=\frac{\sqrt{a}\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{a-\sqrt{a}+1}-\left(2\sqrt{a}+1\right)+1 \\ A=\sqrt{a}\left(\sqrt{a}+1\right)-2\sqrt{a}-1+1 \\ A=a+\sqrt{a}-2\sqrt{a}=a-\sqrt{a} \end{gathered}$$

−(2√a+1)+1A=√a(√a+1)−2√a−1+1A=a+√a−2√a=a−√aA=√a(√a3+1)a−√a+1−√a(2√a+1)√a+1A=√a(√a+1)(a−√a+1)a−√a+1−(2√a+1)+1A=√a(√a+1)−2√a−1+1A=a+√a−2√a=a−√a

Câu 19: Trong mặt phẳng tọa độ Oxy cho →v=(1;1) . Phép tịnh tiến theo →v  biến đường thẳng ∆: x – 1 = 0 thành đường thẳng ∆’ có phương trình là ?

Lời giải:

Ta có $T_{\overrightarrow{v}}\left(\Delta \right)={\Delta }^{\text{'}}\to {\Delta }^{\text{'}}$  song song hoặc trùng với ∆ ⇒ ∆’: x + c = 0

Chọn M(1; 1) ∈ ∆. Gọi M’(x; y) = $T_{\overrightarrow{v}}\left(M\right)\leftrightarrow \overrightarrow{M{M}^{\text{'}}}=\overrightarrow{v}\iff \left\{\begin{array}{c}x-1=1\\ y-1=1\end{array}\right.\iff \left\{\begin{array}{c}x=2\\ y=2\end{array}\right.$ .

→ M’(2; 2) ∈ ∆’ nên 2 + c = 0 ⇔ c = – 2 → ∆’: x – 2 = 0.

Câu 20: Hình thang vuông ABCD ˆA=ˆD=90°, có AB = AD = 2 cm, DC = 4 cm. Tính các góc của hình thang ?

Lời giải:

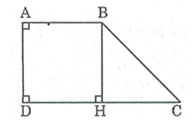
Kẻ BH ⊥ CD

Ta có: AD ⊥ CD (Vì ABCD là hình thang vuông có ˆA=ˆD=90°, ) ⇒ BH // AD

Hình thang ABHD có 2 cạnh bên song song nê HD = AB và BH = AD

AB = AD = 2 cm (gt) ⇒ BH = HD = 2 cm

CH = CD – HD = 4 - 2 = 2 (cm)

⇒ ∆BHC vuông cân tại H

Do đó, ^HBC=ˆC

Lại có: ^HBC=ˆC  = 90° (tính chất tam giác vuông) ⇒ˆC=45°

ˆB+ˆC=180° ( 2 góc trong cùng phía bù nhau) ⇒ˆB=180°−45°=135° .

Câu 21: Tìm GTLN của hàm số y = sinx + cosx ?

Lời giải:

y = sinx + cosx ⇒ y'=cosx−sinx

y'=0⇔cosx−sinx=0⇔cosx=sinx

Mà sin2x+cos2x=1⇒sin2

Với sinx=1√2;cosx=1√2⇒y=1√2+1√2=√2

Với sinx=−1√2;cosx=−1√2⇒y=−1√2−1√2=−√2

Vậy Maxy=√2;Miny=−√2 .

Câu 22: Tổng các nghiệm của phương trình sinxcosx−1=0  trong (0; 2π).

Lời giải:

sinxcosx−1=0 ( x ≠ k2 )

⇒sinx=0⇒x=kπ⇒S={π}

⇒ Tổng các nghiệm là π .

Câu 23: Giải phương trình sau: 3cosx+2|sinx|=2 .

Lời giải:

Đặt cosx = a; $\left|\sin x\right|=b$

Ta có hệ phương trình sau: $\left\{\begin{array}{c}3a+2b=2\\ a^2+b^2=1\end{array}\right.\iff \left\{\begin{array}{c}b=\frac{2-3a}{2}\\ a^2+b^2=1\end{array}\right.$

$$\begin{gathered} \Rightarrow a^2+{\left(\frac{2-3a}{2}\right)}^2=1\Rightarrow 4a^2+{\left(2-3a\right)}^2=4 \\ \iff 13a^2-12a=0\Rightarrow \left[\begin{array}{c}a=0\\ a=\frac{12}{13}\end{array}\right. \end{gathered}$$

a = 0 ⇒ cosx = 0; sinx = ± 1

$\Rightarrow x=\frac{\pi }{2}+k2\pi$ hoặc $x=\frac{\pi }{2}+\left(2k+1\right)\pi$  với x ∈ ℤ

$a=\frac{12}{13}\Rightarrow 2\left|\sin x\right|=2-3\cos x<0$ (loại).

Câu 24: Giải phương trình: ${\left(\sin \frac{x}{2}+\cos \frac{x}{2}\right)}^2+\sqrt{3}\cos x=2$ .

Lời giải:

$$\begin{gathered} {\left(\sin \frac{x}{2}+\cos \frac{x}{2}\right)}^2+\sqrt{3}\cos x=2 \\ \iff 1+2\sin \frac{x}{2}.\cos \frac{x}{2}+\sqrt{3}\cos x=2 \end{gathered}$$

$$\begin{gathered} \iff \sin x+\sqrt{3}\cos x=1 \\ \iff \frac{1}{2}\sin x+\frac{\sqrt{3}}{2}\cos x (chia cả 2 vế cho 2) \end{gathered}$$

$$\begin{gathered} \iff \cos \left(x-\frac{\pi }{6}\right)=\frac{1}{2}=\cos \frac{\pi }{3} \\ \iff x-\frac{\pi }{6}=\frac{\pi }{3}+k\pi \\ \iff x=\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right) \end{gathered}$$

⇔cos(x−π6)=12=cosπ3⇔x−π6=π3+kπ⇔x=π2+kπ(k∈Z)

Câu 25: Cho các mệnh đề:

(1) “ Nếu √3 là số vô tỉ thì 3 là số hữu tỉ”

(2) “ Nếu tứ giác là hình thang có 2 cạnh bên bằng nhau thì nó là hình bình hành”

(3) “ Nếu tứ giác là hình bình hành có hai cạnh bên bằng nhau thì nó là hình thoi”

(4) “ Nếu 3 > 4 thì 1 > 2”

Số mệnh đề có mệnh đề đảo là mệnh đề đúng là ?

Lời giải:

Ta có các mệnh đề đảo:

(1) “ Nếu 3 là số hữu tỉ thì √3  là số vô tỉ”

Vì 2 mệnh đề “3 là số hữu tỉ” và “ √3 là số vô tỉ” đều đúng nên mệnh đề đảo của (1) đúng.

(2) “ Nếu tứ giác là hình bình hành thì nó là hình thang có 2 cạnh bên bằng nhau”

Rõ ràng nếu tứ giác là hình bình hành thì nó chắc chắn có 2 cạnh bên bằng nhau nên mệnh đề đảo của (2) đúng.

(3) “ Nếu tứ giác là hình thoi thì nó là hình bình hành có 2 cạnh bên bằng nhau”, mệnh đề này đúng.

(4) “ Nếu 1 > 2 thì 3 > 4”

Vì 2 mệnh đề 1 > 2 và 3 > 4 đều sai nên mệnh đề đảo của (4) đúng.

Câu 26: Chứng minh: Nếu 1 tam giác vuông cân có độ dài cạnh vuông là số nguyên thì độ dài cạnh huyền là số vô tỉ”.

Lời giải:

Tam giác vuông cân có 2 cạnh góc vuông là x thì cạnh huyền sẽ là x√2  mà √2  là số vô tỉ nên số đo cạnh huyền sẽ là 1 số vô tỉ ⇒ không có tam giác vuông cân nào mà 3 cạnh là số nguyên.

Câu 27: Cho biểu thức: A=(2x−1)2−4(x−1)(x+3)−(5−3x)2 .

a. Rút gọn A.

b. Tính giá trị của biểu thức A khi x=−13 .

Lời giải:

a. A=(2x−1)2−4(x−1)(x+3)−(5−3x)2

A=4x2−4x+1−4x2−8x+12−25+30x−9x2A=−9x2+18x−12A=4x2−4x+1−4x2−8x+12−25+30x−9x2A=−9x2+18x−12

b. x=−13

A=−9.19−18.13−12=−1−6−12=−19

Câu 28: Chứng minh: A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).

Lời giải:

Để chứng minh điều này ta đi chứng minh 2 điều sau:

A ∪ (B ∩ C) ⊂ (A ∪ B) ∩ (A ∪ C) (1)

Và (A ∪ B) ∩ (A ∪ C) ⊂ A ∪ (B ∩ C) (2)

- Chứng minh điều 1:

Giả sử x ∈ A ⇒ x cũng thuộc B và C vì A ∪ (B ∩ C) (*)

⇒ x ∈ (A ∪ B), x ∈ (A ∪ C) ⇒ x ∈ (A ∪ B) ∩ (A ∪ C). Từ (*) và điều này ta ⇒ A ∪ (B ∩ C) ⊂ (A ∪ B) ∩ (A ∩ C). (1)

- Chứng minh điều 2: Giả sử x ∈ (A ∪ B) ⇒ x ∈ (A ∪ C) vì đề cho (A ∪ B) ∩ (A ∪ C).

Từ điều trên ⇒ x ∈ A, B và C ⇒ x ∈ A ∪ (B ∩ C)

Từ điều x ∈ (A ∪ B) ∩ (A ∪ C) mà x ∈ A ∪ (B ∩ C) ⇒ (A ∪ B) ∩ (A ∪ C) ⊂ A ∪ (B ∩ C) (2)

Từ điều 1 và 2 đã được chứng minh như trên ta suy ra được đpcm.

Câu 29: Chứng minh rằng với mọi tập hợp A, B, C: A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).

Lời giải:

Xét x ∈ A ∩ (B ∪ C)

⇒ x ∈ A và x ∈ (B ∪ C)

$$\begin{gathered} \Rightarrow \left\{\begin{array}{c}x\in A\\ \left[\begin{array}{c}x\in B\\ x\in C\end{array}\right.\end{array}\right.\iff \left[\begin{array}{c}\left\{\begin{array}{c}x\in A\\ x\in B\end{array}\right.\\ \left\{\begin{array}{c}x\in A\\ x\in C\end{array}\right.\end{array}\right. \\ \Rightarrow x\in (A\cap B)\cup \left(A\cap C\right)\left(*\right) \end{gathered}$$

Xét x ∈ (A ∩ B) ∪ (A ∩ C)

⇒ x ∈ A ∩ B hoặc x ∈ A ∩ C

⇒ x ∈ A và x ∈ B hoặc x ∈ C

Tức là: x ∈ A ∩ (B ∪ C) (**)

Từ (*); (**) suy ra A ∩ (B ∪ C) = (A .$\cap B)\cup \left(A\cap C\right)$

Câu 30: Phân tích đa thức sau thành nhân tử: 6x2−12xy .

Lời giải:

Ta có: 6x2−12xy=6x(x−2y) .

Câu 31: Cho ∆ABC có ˆB=60° , BC = 8 cm, AB + AC = 12 cm. Tính AB ?

Lời giải:

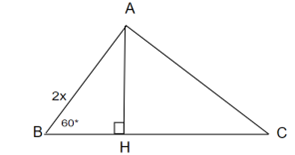
Dựng AH ⊥ BC, đặt AB = x, ta có: AH = x.sinB = x.sin60° = $x\frac{\sqrt{3}}{2}$

HB = x.cos60° = $\frac{x}{2}$ ⇒ HC = BC – HB = 8 - $\frac{x}{2}=\frac{\left(16-x\right)}{2}$

AC = 12 – AB = 12 – x

Trong tam giác vuông AHC:

Hay ${\left(\frac{x\sqrt{3}}{2}\right)}^2+\frac{{\left(16-x\right)}^2}{4}={\left(12-x\right)}^2$

$\iff 3x^2+{\left(16-x\right)}^2=4{\left(12-x\right)}^2$

Giải phương trình này tìm được x = 5. Vậy AB = 5 cm.

Câu 32: Giải phương trình: √2(sinx+cosx)−1=sinx.cosx .

Lời giải:

$\sqrt{2}\left(\sin x+\cos x\right)-1=\sin x.\cos x$ (1)

Đặt t = sinx + cosx, $t\in \left[-\sqrt{2};\sqrt{2}\right]$

$\Rightarrow t^2-1=2\sin x.\cos x$

(1) $\iff \sqrt{2}t-1=\frac{t^2-1}{2}$

$\iff t^2-2\sqrt{2}t+1=0$

$\iff t=\sqrt{2}+1$ (loại) hay $t=\sqrt{2}-1$  (nhận)

$\iff \sin x+\cos x=\sqrt{2}-1$

$\sin \left(x+\frac{\pi }{4}\right)=\frac{\sqrt{2}-1}{\sqrt{2}}$

$\iff x=-\frac{\pi }{4}+\arcsin \left(\frac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi$ hay $x=\frac{3\pi }{4}-\arcsin \left(\frac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi \left(k\in \mathbb{Z}\right)$ .

Câu 33: Giải phương trình: sinx+cosx=1−12sin2x .

Lời giải:

Đặt sinx + cosx = t $\left(\left|t\right|\le \sqrt{2}\right)$

$$\begin{gathered} \Rightarrow {\sin }^{2}x+{\cos }^{2}x+2\sin x.\cos x=t^2 \\ 1+\sin 2x=t^2\Rightarrow {\sin }^{2}x=t^2-1 \end{gathered}$$

Thay vào phương trình đã cho ta được:

$$\begin{gathered} t=1-\frac{1}{2}\left(t^2-1\right) \\ \iff 2t=2-\left(t^2-1\right) \\ \iff t^2+2t-3=0 \\ \iff \left[\begin{array}{c}t=1\left(tm\right)\\ t=-3\left(l\right)\end{array}\right. \end{gathered}$$

Với t = 1, ta có: $\sin x+\cos x=\sqrt{2}\sin \left(x+\frac{\pi }{4}\right)=1$

$$\begin{gathered} \iff \sin \left(x+\frac{\pi }{4}\right)=\frac{1}{\sqrt{2}} \\ \iff \left[\begin{array}{c}x+\frac{\pi }{4}=\frac{\pi }{4}+k2\pi \\ x+\frac{\pi }{4}=\pi -\frac{\pi }{4}+k2\pi \end{array}\right. \\ \iff \left[\begin{array}{c}x=k2\pi \\ x=\frac{\pi }{2}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right) \end{gathered}$$

Câu 34: Cho ∆ABC, trung tuyến AM Chứng minh rằng: AB2+AC2=2AM2+BC22.

Lời giải:

Kẻ AH ⊥ BC (H ∈ BC)

Ta có: AB2+AC2=AH2+BH2+AH2+HC2

=2AH2+(MB−MH)2+(MC+MH)2=2AH2+MB2+MH2−2MB.MH+MC2+MH2+2MC.MH=2AH2+(MB−MH)2+(MC+MH)2=2AH2+MB2+MH2−2MB.MH+MC2+MH2+2MC.MH

=2(AH2+MH2)+2MB2 (vì MB = MC)

=2AM2+2BC24=2AM2+BC22 (ĐPCM)

Vậy AB2+AC2=2AM2+BC22 .

Câu 35: ∆ABC có 2 đường trung tuyến BM và CN vuông góc với nhau. Tìm hệ thức thể hiện quan hệ 3 cạnh của tam giác.

Lời giải:

Ta có công thức đường trung tuyến ma=b2+c22−a24

Chứng minh bổ đề này bằng cách kẻ đường cao hoặc vecto

Ta có: BG⊥CG⇒BC2=BG2+CG2⇔a2=49(m2b+m2c)

a2=49a2+b2+c24⇔5a2=b2+c2

Câu 36: Phương trình cos3x = sinx có bao nhiêu nghiệm?

Lời giải:

cos3x = sinx ⟺ cos3x = cosπ4−x

⇔3x=π2−x+k2π3x=−π2+x+k2π⇔4x=π2+k2π2x=−π2+k2π⇔x=π8+kπ2x=−π4+kπ (k∈ℤ)⇔[3x=π2−x+k2π3x=−π2+x+k2π⇔[4x=π2+k2π2x=−π2+k2π⇔[x=π8+kπ2x=−π4+kπ(k∈Z)

+) 0<π8+kπ2<π⇒−14<k<74⇒k=0.1⇒x=π8;x=5π80<π8+kπ2<π⇒−14<k<74⇒k=0.1⇒x=π8;x=5π8

+) 0<−π4+kπ<π⇒14<k<54⇒k=1⇒x=3π40<−π4+kπ<π⇒14<k<54⇒k=1⇒x=3π4

⇒ Có 3 nghiệm.

Câu 37: Giải phương trình: 1 + tanx = sinx + cosx.

Lời giải:

ĐKXĐ: cosx ≠ 0 $\iff x\ne \frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$

Ta có:

1 + tanx = sinx + cosx

$$\begin{gathered} \iff 1+\tan x=\sin x+\cos x \\ \iff 1+\frac{\sin x}{\cos x}=\sin x+\cos x \\ \iff \frac{\cos x+\sin x}{\cos x}=\sin x+\cos x \\ \iff \left(\sin x+\cos x\right)\left(\frac{1}{\cos x}-1\right)=0 \\ \iff \left[\begin{array}{c}\sin x+\cos x=0\\ \frac{1}{\cos x}=1\end{array}\right. \\ \iff \left[\begin{array}{c}\sqrt{2}\sin \left(x+\frac{\pi }{4}\right)=0\\ \cos x=1\end{array}\right. \\ \iff \left[\begin{array}{c}\sin \left(x+\frac{\pi }{4}\right)=0\\ \cos x=1\end{array}\right. \\ \iff \left[\begin{array}{c}x+\frac{\pi }{4}=k\pi \\ x=k2\pi \end{array}\right. \\ \iff \left[\begin{array}{c}x=-\frac{\pi }{4}+k\pi \\ x=k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right) \end{gathered}$$

Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của các đoạn BC, CD, SO. Tìm giao tuyến của (MNP) với các mặt phẳng (SAB), (SAD), (SBC) và (SCD).

Lời giải:

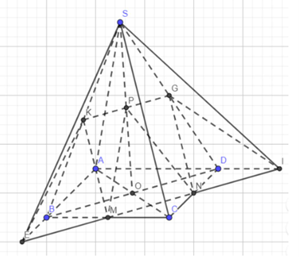
Gọi I, E lần lượt là giao điểm của MN với AD, AB

Qua P  kẻ đường thẳng song song với BD cắt SB, SD lần lượt tại K, G

Ta có:

M, N lần lượt là trung điểm của BC, CD ⇒ MN là đường trung bình của ∆BCD ⇒ MN // BD

Mà KG // BD ⇒ MN // KG ⇒ K, G ∈ (MNP)

Ta có:

+) E=AB∩MN⇒E∈(SAB)∩(MNP)K∈SB;K∈(MNP)⇒K∈(SAB)∩(MNP)⇒(SAB)∩(MNP)=KE

+) I=AD∩MN⇒I∈(SAD)∩(MNP)G∈SD;G∈(MNP)⇒G∈(SAD)∩(MNP)⇒(SAD)∩(MNP)=IG

+)M,K∈(MNP)M,K∈(SBC)⇒(SBC)∩(MNP)=MK

+) N,G∈(MNP)N,G∈(SCD)⇒(SCD)∩(MNP)=NG

Vậy (SAB) ∩ (MNP) = KE; (SAD) ∩ (MNP) = IG; (SBC) ∩ (MNP) = MK; (SCD) ∩ (MNP) = NG.

Câu 39: Phân tích đa thức sau thành nhân tử: 25x2+5x3+x2y .

Lời giải:

Ta có:25x2+5x3+x2y=25x2+5x.x2+y.x2            (Xuất hiện nhân tử chung )

=x225+5x+y

Câu 40: Giải phương trình: sin22x−3cos2x+3=0 .

Lời giải:

sin22x−3cos2x+3=0⇔1−cos22x−3cos2x+3=0⇔−cos22x−3cos2x+4=0⇔cos2x=1(TM)cos2x=−4(L)⇔2x=kπ(k∈ℤ)⇔x=kπ2(k∈ℤ)sin22x−3cos2x+3=0⇔1−cos22x−3cos2x+3=0⇔−cos22x−3cos2x+4=0⇔[cos2x=1(TM)cos2x=−4(L)⇔2x=kπ(k∈Z)⇔x=kπ2(k∈Z)

Câu 41: Giải phương trình: $\sin 2x+3\cos x-2{\sin }^{2}x-3\sin x=0$ .

Lời giải:

$$\begin{gathered} \sin 2x+3\cos x-2{\sin }^{2}x-3\sin x=0 \\ \iff 2\sin x\cos x-2{\sin }^{2}x+3\left(\cos x-\sin x\right)=0 \\ \iff \left(2\sin x+3\right)\left(\cos x-\sin x\right)=0 \\ \iff \left[\begin{array}{c}\sin x=-\frac{3}{2}\left(L\right)\\ \cos x=\sin x\end{array}\right. \\ \iff \cos x=\sin x \\ \iff \cos x=\cos \left(\frac{\pi }{2}-x\right) \\ \iff \left[\begin{array}{c}x=\frac{\pi }{2}-x+k2\pi \\ x=x-\frac{\pi }{2}+k2\pi \end{array}\right. \\ \iff 2x=\frac{\pi }{2}+k2\pi \\ \iff x=\frac{\pi }{4}+k\pi \left(k\in \mathbb{Z}\right) \end{gathered}$$

sin2x+3cosx−2sin2x−3sinx=0⇔2sinxcosx−2sin2x+3(cosx−sinx)=0⇔(2sinx+3)(cosx−sinx)=0⇔[sinx=−32(L)cosx=sinx⇔cosx=sinx⇔cosx=cos(π2−x)⇔[x=π2−x+k2πx=x−π2+k2π⇔2x=π2+k2π⇔x=π4+kπ(k∈Z)

Câu 42: Tính tổng: sin22°+sin24°+sin26°+...+sin284°+sin286°+sin288° .

Lời giải:

sin22°+sin24°+sin26°+...+sin284°+sin286°+sin288°=(sin22°+sin288°)+(sin24°+sin286°)+...+(sin244°+sin246°)sin22°+sin24°+sin26°+...+sin284°+sin286°+sin288°=(sin22°+sin288°)+(sin24°+sin286°)+...+(sin244°+sin246°)

=(sin22°+cos22°)+(sin24°+cos24°)+...+(sin244°+cos244°) 

= 1 + 1 + 1 +....+ 1 = 22 .

Câu 43: Số thập phân nhỏ nhất có 3 chữ số khác nhau và tổng các chữ số bằng 5 là?

Lời giải:

Số thập phân nhỏ nhất có 3 chữ số khác nhau và tổng các chữ số bằng 5 là 0,14.

Vì 0 + 1 + 4 = 5.

Câu 44: Cho các tập hợp X={x∈ℝ|x2−25≤0},A={x∈ℝ|x≤a}  và B={x∈ℝ|x≥b} . Tìm a, b để A ∩ X và B ∩ X là các đoạn có chiều dài lần lượt là 7 và 9.

Lời giải:

A∩X và B ∩ X là các đoạn có chiều dài lần lượt là 7 và 9

 ⇔X=[−5;5];A=[x;a];B[b;x]

A ∩ X = 7 ⇒ a = -5 +7 = 2; B ∩ X = 9 ⇒ b = 5 – 9 = – 4.

Vậy (a; b) = (2; – 4).

Câu 45: Chứng minh a3+b3+c3=3abc .

Lời giải:

Ta có:

$$\begin{gathered} a^3+b^3+c^3-3abc=\left(a^3+b^3\right)+c^3-3abc \\ ={\left(a+b\right)}^3-3ab\left(a+b\right)+c^3-3abc=\left[{\left(a+b\right)}^3+c^3\right]-\left[3ab\left(a+b\right)-3abc\right] \\ =\left(a+b+c\right)\left[{\left(a+b\right)}^2-\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right) \\ =\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right) \end{gathered}$$

Mà a + b + c = 0

$\Rightarrow a^3+b^3+c^3-3abc=0$

$\Rightarrow a^3+b^3+c^3=3abc$ (đpcm).

Câu 46: Cho A = (2m – 1; m + 3) và B = (-4; 5). Tìm m sao cho A ⊂ B.

Lời giải:

Để A ⊂ B thì phải đồng thời xảy ra 2 bất đẳng thức:

2m – 1 ≥ – 1 (hay m ≥ 0) và

2m + 3 ≤ 1 (hay m ≤ – 1)

Nhưng 2 BĐT trên không thể xảy ra đồng thời nên không có giá trị nào của m để A là tập con của B.

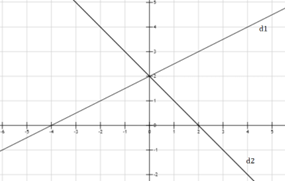
Câu 47: Cho 2 đường thẳng (d1):y=12x+2  và (d2):−x+2 . Vẽ (d₁) và (d₂) trên cùng một hệ trục tọa độ.

Lời giải:

(d1):y=12x+2

x = 0 ⇒ y = 2; y = 0 ⇒ x = -4

(d2):y=−x+2

x = 0 ⇒ y = 2; y = 0 ⇒ x = 2

Câu 48: Chứng minh cosa(1 + cosa)(tana – sina) = sin3a.

Lời giải:

VT = cosa(1 + cosa)(tana – sina)

= (1 + cosa)cosa(tana – sina) = (1 + cosa)(sina – sinacosa)

= sina – sinacosa +sinacosa - sinacos2a=sina−sinacos2a

=sinasin2a=sin3a=VP.

Câu 49: Chứng minh: tana = sinacosa .

Lời giải:

Ta có: sina = đối : huyền mà cosa = kề : huyền

Ta lại có: tana = đối : kề (1)

⇒ sina/ cosa = đối/ huyền : kề/ huyền = đối/ huyền x huyền/ kề

= đối / kề (2)

Từ (1) và (2) ⇒ tana = sina/ cosa ⇒ đpcm.

Câu 50: Một tòa nhà có n tầng, các tần được đánh số từ 1 đến n theo thứ tự từ dưới lên trên. Có 4 thang máy đang ở tầng 1. Biết rằng mỗi thang máy có thể dừng ở đúng 3 tầng (không kể tầng 1) và 3 tầng này không là 3 tầng số nguyên liên tiếp với 2 tầng bất kì (khác tầng 1) của tòa nhà luôn có 1 thang máy dừng được ở cả 2 tầng này. Hỏi GTLN của n là bao nhiêu?

Lời giải:

Giả sử 4 thang máy là A, B, C, D

Do 2 thang máy bất kì thì luôn có 1 thang được dừng nên

- Khi bốc 2 tầng 2 và 3 có 1 thang dừng được giả sử đó là A nên tầng 4 không phải thang A dừng.

- Khi bốc 2 tầng 3 và 4 thì có thang dừng được giả sử đó là B nên tầng 5 không phải thang A dừng.

- Khi bốc 2 tầng 4 và 5 thì có thang dừng được giả sử đó là C nên tầng 6 không phải thang A dừng.

- Khi bốc 2 tầng 5 và 6 thì có thang dừng được giả sử đó là D

- Khi bốc 2 tầng 5 và 7 thì có thang dừng được khi đó không thể là A, B, C vì sẽ dừng 4 (mâu thuẫn) thang D không thể ở tầng 7 do đó không thể ở 3 tầng liên tiếp.

Vậy tòa nhà có tối đa 6 tầng.

Câu 51: Tính $E=\frac{1}{1.7}+\frac{1}{7.13}+\frac{1}{13.19}+\mathrm{...}+\frac{1}{31.37}$ .

Lời giải:

$$\begin{gathered} E=\frac{1}{1.7}+\frac{1}{7.13}+\frac{1}{13.19}+\mathrm{...}+\frac{1}{31.37} \\ E=\frac{1}{6}\left(\frac{6}{1.7}+\frac{6}{7.13}+\frac{6}{13.19}+\mathrm{...}+\frac{6}{31.37}\right) \\ E=\frac{1}{6}\left(1-\frac{1}{7}+\frac{1}{7}-\frac{1}{13}+\frac{1}{13}-\frac{1}{19}+\mathrm{...}+\frac{1}{31}-\frac{1}{37}\right) \\ E=\frac{1}{6}\left(1-\frac{1}{37}\right)=\frac{1}{6}.\frac{36}{37}=\frac{6}{37} \end{gathered}$$

Vậy $E=\frac{6}{37}$ .

Câu 52: Giải phương trình $\sqrt{3}\cos \left(x+\frac{\pi }{2}\right)+\sin \left(x-\frac{\pi }{2}\right)=2\sin 2x$ .

Lời giải:

Ta có $\cos \left(x+\frac{\pi }{2}\right)=-\sin x$  và $\sin \left(x-\frac{\pi }{2}\right)=-\cos x$

Do đó phương trình

$\iff -\sqrt{3}\sin x-\cos x=2\sin 2x\iff \sqrt{3}\sin x+\cos x=-2\sin 2x$

$$\begin{gathered} \iff \frac{\sqrt{3}}{2}\sin x+\frac{1}{2}\cos x=-\sin 2x\iff \sin \left(x+\frac{\pi }{6}\right)=-\sin 2x\iff \sin \left(x+\frac{\pi }{6}\right)=\sin \left(-2x\right) \\ \iff \left[\begin{array}{c}x+\frac{\pi }{6}=-2x+k2\pi \\ x+\frac{\pi }{6}=\pi +2x+k2\pi \end{array}\right.\iff \left[\begin{array}{c}x=-\frac{\pi }{18}+k\frac{2\pi }{3}\\ x=-\frac{5\pi }{6}-k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right) \end{gathered}$$

Xét nghiệm $x=-\frac{5\pi }{6}-k2\pi \underset{k\in \mathbb{Z},k^{\text{'}}\in \mathbb{Z}}{\overset{k=-1-k^{\text{'}}}{\to }}x=\frac{7\pi }{6}+k^{\text{'}}2\pi$ .

Vậy phương trình có nghiệm $x=-\frac{\pi }{18}+k\frac{2\pi }{3},x=\frac{7\pi }{6}+k^{\text{'}}2\pi \left(k,k^{\text{'}}\in \mathbb{Z}\right)$ .