Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 27) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Trên các cạnh AB, BC, CA của ∆ABC lần lượt lấy 2, 4, n (n > 3)
Câu 7: Trên các cạnh AB, BC, CA của ∆ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n + 6 điểm đã cho là 247.
Lời giải:
Nhận xét: Mỗi tam giác được lập thành do một cách chọn 3 điểm sao cho 3 điểm đó không thẳng hàng tức là không cùng nằm trên một cạnh của ∆ABC.
Chọn ngẫu nhiên 3 điểm từ n + 6 điểm đã cho có: C3n+6 cách.
Chọn 3 điểm chỉ nằm trên đúng 1 cạnh của ∆ABC có: C34+C3n (cách).
Số tam giác lập thành là: C3n+6−(C34+C3n)=247
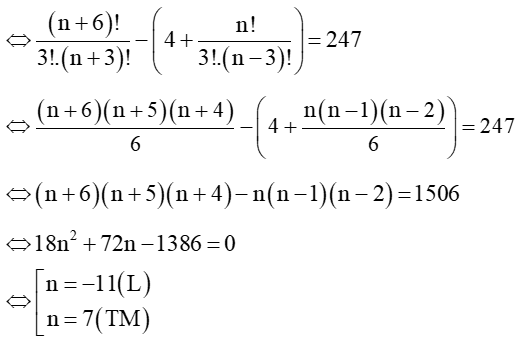
Vậy n = 7.
Xem thêm các bài giải Tổng hợp kiến thức môn Toán hay, chi tiết khác:
Câu 1: Cho x ∈ ℕ. Hãy chứng minh x2+1 không chia hết cho 4.
Câu 2: Cho n ∈ ℕ, chứng minh rằng n2+n+1 không chia hết cho 4 và không chia hết cho 5.
Câu 3: Cho phương trình cotx=√3 . Tính các nghiệm của phương trình ?
Câu 4: Giá trị của M=cos215+cos225+cos235+cos245+cos2105+cos2115+cos2125 là ?
Câu 6: ∆ABC có ˆA=120° . Khẳng định nào sau đây đúng ?
Câu 8: Tính GTLN của diện tích 1 tam giác biết 3 trong 2 cạnh của nó là 5 và 8.
Câu 9: Tìm m để phương trình 3sinx – 4cosx = 2m có nghiệm ?
Câu 12: Xác định a để đa thức 10x2−7x+a chia hết cho 2x – 3.
Bài viết cùng bài học:




