Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5)

Ngọc Nguyễn Ngày: 13-06-2023 Tổng hợp kiến thức

646

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5)

Bài 1: Hai góc tương ứng là gì?

Lời giải:

Hai góc tương ứng là hai góc của hai tam giác khác nhau.

Hai góc đó bằng nhau và nằm trong hai tam giác bằng nhau.

Bài 2: Cho tam giác ABC, lấy D là trung điểm của AC. Từ A vẽ đường thẳng song song với BC, cắt BD tại E. Tại cạnh BC lấy điểm M sao cho DM cắt AE tại N. Chứng minh rằng:

a) $\hat{A E D} = \hat{C B D}$

b) $\hat{D N E} = \hat{D M B}$

c) $\hat{B A D} = \hat{D C E}$ .

Lời giải:

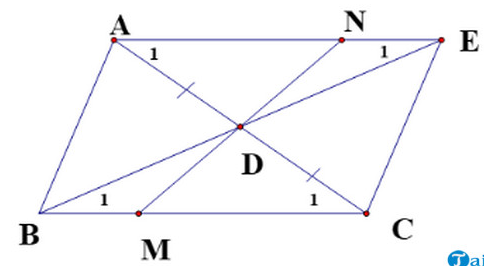
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 1)

a) Chứng minh: $\hat{A E D} = \hat{C B D}$

Xét tam giác ADE và tam giác CDB, có:

$\hat{D A E} = \hat{D C B}$ (vì hai góc so le trong)

DA = DC (D là trung điểm của AC)

$\hat{A D E} = \hat{C D B}$ (hai góc đối đỉnh)

→ Tam giác ADE = tam giác CDB (g.c.g)

→ $\hat{A E D} = \hat{C B D}$ (điều phải chứng minh)

Câu b); câu c): Học sinh tự giải (tương tự như phương pháp giải các câu trên).

Bài 3: Có bao nhiêu phân số thập phân có tử số là 3, lớn hơn $\frac{1}{34}$ và nhỏ hơn $\frac{1}{8}$ .

Lời giải:

Gọi số đó là x

Ta có :

$\frac{1}{34} < x < \frac{1}{8} \Rightarrow \frac{4}{136} < x < \frac{17}{136} \Rightarrow x \in \{\frac{5}{136}; \frac{6}{136}; \frac{7}{136}; \frac{8}{136}; \frac{9}{136}; \frac{10}{136}; \frac{11}{136}; \frac{12}{136}; \frac{13}{136}; \frac{14}{136}; \frac{15}{136}; \frac{16}{136}\} \Rightarrow x \in \{\frac{5}{136}; \frac{3}{68}; \frac{7}{136}; \frac{1}{17}; \frac{9}{136}; \frac{5}{68}; \frac{11}{136}; \frac{3}{34}; \frac{13}{136}; \frac{7}{68}; \frac{15}{136}; \frac{2}{17}\}$

Vậy có 2 phân số có tử số là 3, lớn hơn $\frac{1}{34}$ và nhỏ hơn $\frac{1}{8}$ .

Bài 4: Tìm x: $9 {(x + 1)}^{2} - (3 x - 2) (3 x + 2) = 10$

Lời giải:

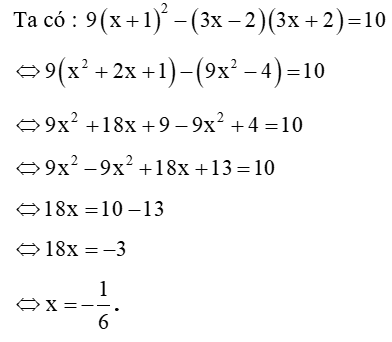
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 2)

Bài 5: Tú và Hiếu có 40 viên bi, sau khi Hiếu cho Tú 2 viên thì số bi của Hiếu bằng số bi của Tú. Hỏi ban đầu Tú có bao nhiêu viên.

Lời giải:

Số bi ban đầu của Tú là

40 : 2 – 2 = 18 (viên bi).

Bài 6: Xác định số đo góc nhỏ nhất của một tứ giác lồi, biết rằng số đo 4 góc lập thành một cấp số cộng và góc lớn nhất bằng 5 lần góc nhỏ nhất.

A. 30^o

B. 45^o

C. 15^o

D. 60^o

Lời giải:

Chọn A

Gọi d = 2a là công sai. Bốn số phải tìm là:

A = (x - 3a); B = (x - a); C = (x + a); D = (x + 3a).

Tổng số đo 4 góc của 1 tứ giác bằng 360^o

Ta có hệ phương trình:

Số đo góc nhỏ nhất là : 90 – 3 . 20 = 30.

Bài 7: Xác định 4 góc của một tứ giác lồi, biết rằng đo 4 góc lập thành 1 cấp số cộng và góc lớn nhất bằng 5 lần góc nhỏ nhất?

Lời giải:

Chẳng hạn

Gọi a số đo của tứ giác ABCD

Vì các góc lập thành cấp số cộng (số đo góc lớn hơn số đo góc nhỏ hơn bằng một số)

Gọi d là khoảng chênh lệch số đo giữa các góc (công sai của cấp số cộng, lớp 11 mới học)

Theo đề ta có

a + (a + d) + (a + 2d) + (a + 3d) = 360^o

4a + 6d = 360

hay 2a + 3d = 180 (1)

Vì góc lớn nhất gấp 5 lần góc nhỏ nhất nên

a + 3d = 5a (2)

Từ (2) suy ra 3d = 5a - a = 4a

Thau vào (1):

2a + 3d = 2a + 4a = 180

6a = 180 suy ra a = 30

Vậy số đo góc A là 30 độ

số đo góc B là 70 độ

góc C = 70 + 40 = 110 độ

và góc D = 110 + 40 = 150 độ

Bài 8: Hiện nay bố 32 tuổi, con 5 tuổi. Hỏi mấy năm nữa thì tuổi bố gấp 4 lần tuổi con?

Lời giải:

Hiệu số tuổi của hai bố con là:

32 – 5 = 27 (tuổi)

Tuổi của con lúc tuổi bố gấp 4 lần tuổi con là:

27 : (4 - 1) = 27 : 3 = 9 (tuổi)

Số năm cần tìm là:

9 – 5 = 4 (năm)

Bài 9: Tìm số thực a biết: chia x – 2 dư 3

Lời giải:

Để số dư của phép chia là 3 thì 3a – 12 = 3 ⇔ a = 5.

Bài 10: Trong mặt phẳng Oxy cho đường thẳng 2x - y + 1 = 0. Để phép tịnh tiến theo vecto $\vec{v}$ biến đường thẳng dthành chính nó thì $\vec{v}$ phải là vecto nào trong các vecto sau?

A. (1; 2)

B. (2; -1)

C. (2; 1)

D. (0; 1)

Lời giải:

Đáp án A

Vecto tịnh tiến cùng phương với d. Một vecto chỉ phương của d là $\vec{u_{d}} = (1; 2)$ .

Bài 11: 36dm =.......m

Lời giải:

36dm = 3,6 m

Bài 12: Một tổ công nhân có 12 người. Cần chọn 3 người, một người làm tổ trưởng, một tổ phó và một thành viên. Hỏi có bao nhiêu cách chọn?

A. 1320

B. 12!

C. 230

D. 1230

Lời giải:

Đáp án A

Số cách chọn 3 người làm tổ trưởng, tổ phó, thành viên là một chỉnh hợp chập 3 của 12 phần tử: $A_{12}^{3} = 1320$ cách

Số cách chọn là 1320

Bài 13: Cho lục giác ABCDEF. Có bao nhiêu vectơ khác vectơ – không có điểm đầu và điểm cuối là đỉnh của lục giác.

A. 20

B. 12

C. 30

D. 16

Lời giải:

Hai điểm phân biệt, chẳng hạn A, B ta xác định được hai vectơ khác vectơ – không là $\vec{A B}; \vec{B A}$ .

Một vectơ khác vectơ – không được xác định bởi 2 điểm phân biệt. Do đó có 30 cách chọn 2 điểm trong 4 điểm của tứ giác (có tính thứ tự các điểm) nên có thể lập được 30 vectơ.

Bài 14: Cho tam giác ABC có trọng tâm G. Khi đó:

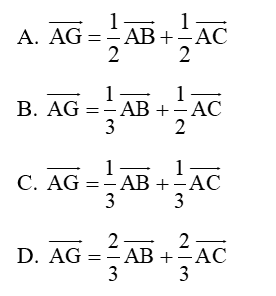
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 4)

Lời giải:

$\begin{array}{l} \vec{G A} + \vec{G B} + \vec{G C} = \vec{0} \Leftrightarrow \vec{A G} = \vec{G B} + \vec{G C} \\ \Leftrightarrow \vec{A G} = \vec{A B} - \vec{A G} + \vec{A C} - \vec{A G} \Leftrightarrow 3 \vec{A G} = \vec{A B} + \vec{A C} \Leftrightarrow \vec{A G} = \frac{1}{3} \vec{A B} + \frac{1}{3} \vec{A C} \end{array}$

Chọn C

Bài 15: Cho tam giác ABC có trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh BC, CA, AB. Phép vị tự tâm G biến tam giác ABC thành tam giác A’B’C’ có tỉ số vị tự bằng bao nhiêu?

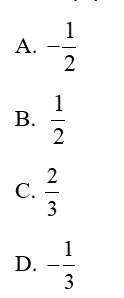
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 5)

Lời giải:

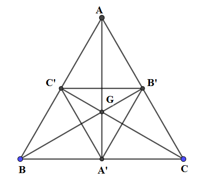
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 6)

Vì $\vec{G A'} = - \frac{1}{2} \vec{G A}; \vec{G B'} = - \frac{1}{2} \vec{G B}; \vec{G C'} = - \frac{1}{2} \vec{G C}$ nên phép vị tự tâm G biến tam giác ABC thành tam giác A’B’C’ có tỉ số vị tự bằng $- \frac{1}{2}$

Chọn: A

Bài 16: Tổng tất các nghiệm thuộc đoạn $[0,10 π]$ của phương trình $\sin^{2} 2 x + 3. \sin 2 x + 2 = 0$

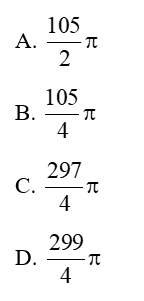
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 7)

Lời giải:

Phương trình: $s i n^{2} 2 x + 3 s i n 2 x + 2 = 0$

$\Leftrightarrow [\begin{matrix} s i n 2 x = - 1 \\ s i n 2 x = - 2 (V L) \end{matrix} \Leftrightarrow s i n 2 x = - 1 \Leftrightarrow x = - \frac{π}{4} + k π, k \in ℤ$

Ta có: $x \in [0; 10 π]$

$\Rightarrow 0 \leq - \frac{π}{4} + k π \leq 10 π \Rightarrow \frac{π}{4} \leq k π \leq \frac{41 π}{4} \Rightarrow \frac{1}{4} \leq k \leq \frac{41}{4}$

Mà $k \in ℤ$ nên $k \in \{1; 2; 3; 4; 5; 6; 7; 8; 9; 10\}$

Khi đó các nghiệm của phương trình là: $x \in \{\frac{3 π}{4}; \frac{7 π}{4}; \frac{11 π}{4}; \frac{15 π}{4}; ...; \frac{39 π}{4}\}$

Vậy tổng các nghiệm của phương trình là: $\frac{3 π}{4} + \frac{7 π}{4} + \frac{11 π}{4} + \frac{15 π}{4} + ... + \frac{39 π}{4} = \frac{105 π}{2}$

Chọn đáp án A.

Bài 17: Tính tổng T các nghiệm của phương trình sin2x – cosx = 0 trên $[0; 2 π] .$

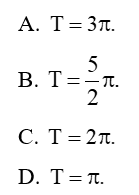
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 8)

Lời giải:

Ta có

$\sin 2 x - \cos x = 0 \Leftrightarrow \sin 2 x = \cos x \Leftrightarrow \sin 2 x = \sin (\frac{π}{2} - x) \Leftrightarrow [\begin{matrix} 2 x = \frac{π}{2} - x + k 2 π \\ 2 x = π - (\frac{π}{2} - x) + k 2 π \end{matrix} \Leftrightarrow [\begin{matrix} x = \frac{π}{6} + \frac{k 2 π}{3} \\ x = \frac{π}{2} + k 2 π \end{matrix}$

Vì $x \in [0; 2 π]$ suy ra

$\Leftrightarrow [\begin{matrix} 0 \leq \frac{π}{6} + \frac{k 2 π}{3} \leq 2 π \\ 0 \leq \frac{π}{2} + k 2 π \leq 2 π \end{matrix} \Leftrightarrow [\begin{matrix} - \frac{1}{4} \leq k \leq \frac{11}{4} \Rightarrow k \in \{0; 1; 2\} \\ - \frac{1}{4} \leq k \leq \frac{3}{4} \Rightarrow k \in \{0\} \end{matrix}$

Từ đó suy ra các nghiệm của phương trình trên đoạn $[0; 2 π]$ là $\frac{π}{6}; \frac{5 π}{6}; \frac{3 π}{2}; \frac{π}{2} \to T = 3 π .$

Đáp án cần chọn là: A

Bài 18: Thực hiện các phép tính:

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 9)

Lời giải:

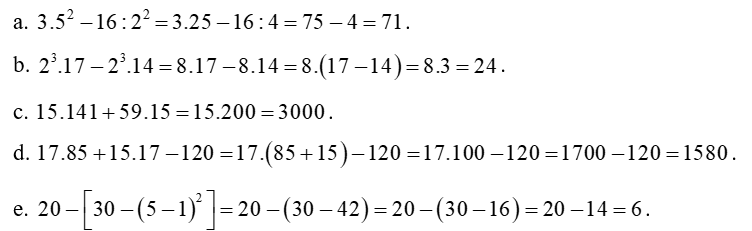
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 10)

Bài 19: Từ một điểm A nằm bên ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC với đường tròn. Đường thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M.

1. Xác định hình tính của tứ giác AMON.

2. Điểm A phải cách O một khoảng là bao nhiêu để MN là tiếp tuyến của (O)?

Lời giải:

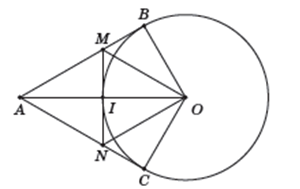
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 11)

1. Xét tứ giác AMON ta có

$\{\begin{matrix} A M / / O N (cung. v u o n g . g o c . v o i . O B) \\ A N / / O M (cung. v u o n g . g o c . v o i . O C) \end{matrix}$

Do đó AMON là hình bình hành

Mặt khác, xét hai tam giác vuông

$Δ O B M$ và $Δ O B M$ ta có

$\{\begin{matrix} O B = O C = R \\ \hat{M O B} = \hat{N O C} (c u n g . p h u . v o i . g o c . \hat{M O N}) \end{matrix}$

Do đó $Δ O B M = Δ O C N \Rightarrow O M = O N$

Vậy AMON là hình thoi

2. Để MN tiếp xúc với (O; R) thì $d (O; M N) = R \Leftrightarrow O I = R \Leftrightarrow O A = 2 R$

Bài 20: Cho hình bình hành ABCD có AB = 2AD. Gọi E, F thứ tự là trung điểm của AB và CD

a) Các tứ giác AEFD, AECF là hình gì? Vì sao?

b) Gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật.

Lời giải:

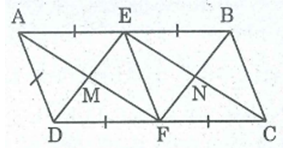
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 12)

a) Ta có: $A E = D E = \frac{1}{2} A B$ và AE // DF

→ tứ giác AEFD là hình bình hành

Có thêm $A E = A D = \frac{1}{2} A B$

→AEFD là hình thoi (dấu hiệu nhận biết hình thoi)

AE // FC và AE = FC ( vì cùng $= \frac{1}{2} A B$ )

→ AECF là hình bình hành

b) Tứ giác AECF là hình bình hành nên EN // MF(1)

Chứng minh tương tự câu a tứ giác EBFN là hình bình hành

→ ME // FN(2)

Từ (1) và (2) suy ra EMFN là hình bình hành (3)

Tứ giác AEFD là hình thoi nên suy ra $AF ⊥ D E$

$\to \hat{EMF} = 90^{\circ}$ (4)

Từ (3) và (4) suy ra EMFN là hình chữ nhật

Bài 21: Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau và có BC = 3, góc $\hat{B A C} = 30^{0}$ . Tính

diện tích tam giác ABC.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 13)

Lời giải:

Vì $B M ⊥ C N \to 5 a^{2} = b^{2} + c^{2}$ . (Áp dụng hệ quả đã có trước)

Trong tam giác ABC, ta có

$a^{2} = b^{2} + c^{2} - 2 b c . \cos A = 5 a^{2} - 2 b c . \cos A \to b c = \frac{2 a^{2}}{\cos A}$

Khi đó $S = \frac{1}{2} b c \sin A = \frac{1}{2} . \frac{2 a}{\cos A} . \sin A = a^{2} t = 3 \sqrt{3}$

Chọn A

Bài 22: Chứng minh rằng: nếu 1 tam giác có 2 đường trung tuyến vuông góc với nhau thì tổng các bình phương của 2 đường trung tuyến này bằng bình phương của đường trung tuyến thứ ba.

Lời giải:

Giả sử có hai đường trung tuyến BE và CF vuông góc với nhau, AD là đường trung tuyến thứ ba. Ta cần chứng

minh $A D^{2} = B E^{2} + C F^{2}$

Trên tia đối của tia EF lấy điểm K sao cho EF = FK

Tứ giác AKCF có hai đường chéo cắt nhau tại trung điểm E của mỗi đường nên AKCF là hình bình hành → AK // FC.

Mà $F C ⊥ B E$ nên $B E ⊥ A K$ (*)

Ta có: F là trung điểm của AB, E là trung điểm của AC nên EF là đường trung bình của $Δ A B C \to E F = \frac{1}{2} B C$ và EF // BC hay EK // BD (1)

Mà $B D = \frac{1}{2} B C$ (gt) nên EF = BD → EK = BD (do EF = EK theo cách chọn điểm phụ) (2)

Từ (1) và (2) suy ra EKDB là hình bình hành → EB // DK (**)

Từ (*) và (**) suy ra → $D K ⊥ A K$ vuông tại K $\to A K^{2} + K D^{2} = A D^{2}$ (theo định lý Py-ta-go)

Mà AK = FC (do AKCF là hình bình hành) và KD = BE (do EKDB là hình bình hành) nên $A D^{2} = B E^{2} + C F^{2}$ (đpcm)

Bài 23: Tam giác ABC có hai trung tuyến AM và BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo AM và BN

Lời giải:

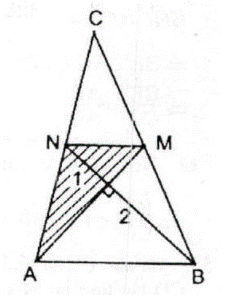
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 14)

Tứ giác ABMN có hai đường chéo vuông góc.

$S_{A B M N} = \frac{1}{2} A M . B N$

$Δ A B M$ và $Δ A M C$ có chung chiều cao kẻ từ A cạnh đáy BM = MC

$\to S_{A B M} = S_{A M C} = \frac{1}{2} S_{A B C}$

$Δ M A N$ và $Δ M N C$ có chung chiều cao kẻ từ M, cạnh đáy AN = NC

$\begin{array}{l} \to S_{M A N} = S_{M N C} = \frac{1}{2} S_{A M C} = \frac{1}{4} S_{A B C} \\ S_{A B M N} = S_{A B M} + S_{M N A} = \frac{1}{2} S_{A B C} + \frac{1}{4} S_{A B C} = \frac{3}{4} S_{A B C} \\ \to S_{A B C} = \frac{4}{3} S_{A B M N} = \frac{4}{3} . \frac{1}{2} . A M . B N = \frac{2}{3} A M . B N \end{array}$

Bài 24: Tìm ảnh của đường tròn (C) qua phép quay tâm O, góc quay -90° biết: (C): (x + 4)² + (y - 1)² = 16

Lời giải:

Từ (C), ta có tâm I(-4; 1) và bán kính R = 4. Khi đó: $Q_{(O, - 90 °)} (I) = I' (1; 4)$ và bán kính

R' = R = 4

Vậy: $Q_{(O, - 90 °)} (C) = (C') : {(x - 1)}^{2} + {(y - 4)}^{2} = 16$

Bài 25: Tìm ảnh của đường tròn (C): ${(x - 1)}^{2} + {(y + 2)}^{2} = 9$ qua phép quay Q( I; 90°) với I(3; 4)

Lời giải:

⇒Ảnh của (C) là đường tròn tâm B bán kính R = 3 với B là ảnh của A qua phép quay Q(I; 90⁰)

Ta có: $\{\begin{matrix} x_{B} = 3 + (1 - 3) c o s 90^{0} - (- 2 - 4) s i n 90^{0} \\ y_{B} = 4 + (1 - 3) s i n 90^{0} + (- 2 - 4) c o s 90^{0} \end{matrix}$

$\Rightarrow \{\begin{matrix} x_{B} = 9 \\ y_{B} = 2 \end{matrix} \Rightarrow B (9; 2)$

Vậy phương trình ảnh là: ${(x - 9)}^{2} + {(y - 2)}^{2} = 3$

Bài 26: Cho đồ thị chuyển động của hai xe được mô tả trên hình vẽ.

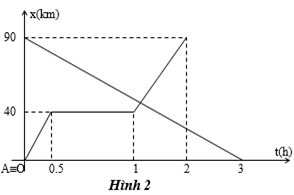
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 15)

a. Hãy nêu đặc điểm chuyển động của hai xe.

b. Tình thời điểm hai xe gặp nhau, lúc đó mỗi xe đi được quãng đường là bao nhiêu ?(Hình 2)

Lời giải:

a, Xe 1 chia làm ba giai đoạn

Giai đoạn 1:

Ta có $v_{1} = \frac{x_{2} - x_{1}}{t_{2} - t_{1}} = \frac{40 - 0}{0,5 - 0} = 80$ km/h

Xe chuyển động theo chiều dương với 80 km/h xuất phát từ gốc tọa độ

Phương trình chuyển động:

$x_{g d 1} = 80 t (0 \leq t \leq 0,5)$

Giai đoạn 2:

Ta có $v_{2} = \frac{x_{3} - x_{4}}{t_{3} - t_{4}} = \frac{40 - 40}{1 - 0,5} = 0$ km/h

Xe đứng yên tại vị trí cách gốc tọa độ là 40km trong khoảng thời gian 0,5h

Phương trình chuyển động gđ 2:

$x_{g d 2} = 40 + 0 (t - 0,5) (0,5 \leq t \leq t)$

Giai đoạn 3

Ta có $v_{g d 3} = \frac{x_{5} - x_{4}}{t_{5} - t_{4}} = \frac{90 - 40}{2 - 1} = 50$ km/h

Xe vẫn chuyển động theo chiều dương với 50 km/h xuất phát cách gốc tọa độ 40km và xuất phát sau gốc thời gian là 1h

Phương trình chuyển động:

$x_{3} = 40 + 50 (t - - 1) (1 \leq t \leq 2)$

Đới với xe 2:

Ta có $v = \frac{x_{2} - x_{1}}{t_{2} - t_{1}} = \frac{0 - 90}{3 - 0} = - 30$ km/h

Vậy xe 2 chuyển động theo chiều âm với vận tốc -30 km/h xuất phát cách gốc tọa độ là 90km, cùng gốc thời gian

$x_{x 2} = 90 - 30 t (0 \leq t \leq 3)$

b; Từ hình vẽ ta nhận thấy hai xe gặp nhau ở giai đoạn 3 của xe một

Ta có:

$x_{x 2} = x_{3} \Rightarrow 90 - 30 t = 40 + 50 (t - 1) \Rightarrow t = \frac{5}{4} h = 1,25 h$

Vậy sau 1h15 phút hai xe gặp nhau và xe hai đi được quãng đường:

$s_{2} = v t = 30.1,25 = 37,5 k m$

Xe một đi được quãng đường

$s_{1} = 90 - 37,5 = 52,5 k m$

Bài 27: Cho đồ thị chuyển động của hai xe được mô tả như hình vẽ. (Hình 1). Hãy nêu đặc điểm chuyển động của mỗi xe và viết phương trình chuyển động

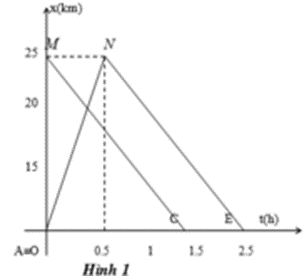
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 16)

Lời giải:

Đối với xe 1 chuyển động từ A đến N rồi về E

Xét giai đoạn 1 từ A đến N: $v_{1} = x_{N} - x_{A} t_{N} - t_{A} = 25 - 00,5 - 0 = 50$ km/h

Xe một chuyển động từ gốc tọa độ đến N theo chiều dương với vận tốc 50km/h

Phương trình chuyển động $x_{1 g d 1} = 50 t$ ĐK: $0 \leq t \leq 0,5$

Xét giai đoạn hai từ N về E: $v_{2} = x_{E} - x_{N} t_{E} - t_{N} = 0 - 252,5 - 0,5 = - 12,5$ km/h

Giai đoạn hai chuyển động từ N về E theo chiều âm có vận tốc -12,5km/h và xuất phát cách gốc tọa độ 25km và sau 0,5h xo với gốc tọa độ

Phương trình chuyển động $x_{2} = 25 - 12,5 (t - 0,5)$ ĐK: $0,5 \leq t \leq 2,5$

Đối với xe 2 chuyển động từ M về C với

$v = x_{C} - x_{M} t_{C} - t_{M} = 0 - 25 1,5 - 0 = - 503$ km/h

Chuyển động theo chiều âm, cách gốc tọa độ 25km: $x_{2} = 25 - 503 t$ ĐK: $0 \leq t \leq 1,5$

Bài 28: Cho a, b, c > 0 và a + b + c = 1. tìm GTLN của $\frac{a}{a + 1} + \frac{b}{b + 1} + \frac{c}{c + 1}$

Lời giải:

$\frac{a}{a + 1} + \frac{b}{b + 1} + \frac{c}{c + 1} = a - \frac{a^{2}}{a + 1} + b - \frac{b^{2}}{b + 1} + c - \frac{c^{2}}{c + 1} = 1 - (\frac{a^{2}}{a + 1} + \frac{b^{2}}{b + 1} + \frac{c^{2}}{c + 1})$

Áp dụng BĐT Cauchy dạng phân thức $\frac{a^{2}}{a + 1} + \frac{b^{2}}{b + 1} + \frac{c^{2}}{c + 1} \geq \frac{{(a + b + c)}^{2}}{a + b + c + 3} = \frac{1}{1 + 3} = \frac{1}{4}$

$\to \frac{a^{2}}{a + 1} + \frac{b^{2}}{b + 1} + \frac{c^{2}}{c + 1} \leq 1 - \frac{1}{4} = \frac{3}{4}$

→ GTLN $= \frac{3}{4}$ Dấu “=” xảy ra khi $a = b = c = \frac{1}{3}$

Bài 29: Tính giá trị nhỏ nhất của $A = \frac{1}{a} + \frac{1}{b} + \frac{1}{c}$ với a, b, c > 0 và $a + b + c = 3 a b c$

Lời giải:

Từ điều kiện

$a + b + c = 3 a b c \Rightarrow A = \frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{a b + b c + a c}{a b c} = \frac{3 (a b + b c + a c)}{a + b + c}$ (1)

Theo hệ quả của BĐT AM-GM

$\begin{array}{l} a^{2} b^{2} + b^{2} c^{2} + c^{2} a^{2} \geq a b c (a + b + c) \\ \Leftrightarrow {(a b + b c + a c)}^{2} \geq 3 a b c (a + b + c) = {(a + b + c)}^{2} \\ \Leftrightarrow a b + b c + a c \geq a + b + c (2) \end{array}$

Từ (1) và (2) $\Rightarrow A \geq 3$

Do đó $A_{\min} = 3 \Leftrightarrow a = b = c = 1$

Bài 30: Xét các mệnh đề sau

(I): Véc tơ – không là véc tơ có độ dài bằng 0.

(II): Véc tơ – không là véc tơ có nhiều phương.

A. Chỉ (I) đúng.

B. Chỉ (II) đúng.

C. (I) và (II) đúng.

D. (I) và (II) sai.

Lời giải:

Đáp án: C

Véc tơ – không là véc tơ có điểm đầu, điểm cuối trùng nhau nên có độ dài bằng 0.

Véc tơ – không cùng phương với mọi véc tơ.

Bài 31: Tính tổng các số lẻ liên tiếp từ 1 đến 99

Lời giải:

Số lẻ nhỏ nhất là 1

Số lẻ lớn nhất là 99

Khoảng cách giữa hai số lẻ liên tiếp là 2

Số số hạng là: $(99 - 1) : 2 + 1 = 98 : 2 + 1 = 50$

Tổng là: $(99 + 1) \times 50 : 2 = 100 \times 50 : 2 = 2500$

Đáp số: 2500

Bài 32: Tổng các số tự nhiên từ 1 đến 99 là:

A. 4900

B. 4950

C. 5000

D. 5050

Lời giải:

CTTQ: $(n (n + 1)) : 2$

Ta có: $(99 (99 + 1)) : 2 = 4950$

Vậy, đáp án đúng là B.

Bài 33: Tổng các ước tự nhiên của số 75 là ?

Lời giải:

Các ước tự nhiên của số 75 là: 1, 3, 5, 15, 25, 75

→ Tổng các ước tự nhiên của số 75 là: $1 + 3 + 5 + 15 + 25 + 75 = 124$

Bài 34: Số ước tự nhiên của 75 là bao nhiêu ?

Lời giải:

75 = 31 . 52

Số ước tự nhiên của 75 là: ( 1 + 1 ) . ( 2 + 1 ) = 6 (ước)

Bài 35: Cho a, b thuộc N. Chứng tỏ rằng nếu 5a + 3b và 13a + 8b cùng chia hết cho 2012 thì a và b cũng chia hết cho 2012

Lời giải:

a có: 5a + 3b chia hết cho 2012 → 13(5a + 3b) chia hết cho 2012

→ 65 a + 39b chia hết cho 2012 (1)

Lại có: 13a + 8b chia hết cho 2012 → 5(13a + 8b) chia hết cho 2012

→ 65 a + 40b chia hết cho 2012 (2)

Từ (1)(2) → (65a + 40b) – (65a + 39b) chia hết cho 2012

→ b chia hết cho 2012

Tương tự → a chia hết cho 2012

Vậy a, b cũng chia hết cho 2012

Bài 36: Số nào sau đây: 13, 15, 17, 19 là hợp số?

A. 13

B. 15

C. 17

D. 19.

Lời giải:

Đáp án đúng là: B

Số 15 là hợp số.

Bài 37: Cho tam giác ABC vuông tại A có AB = 3cm; AC = 4cm, đường cao AH.

a) Tính BC,AH;

b) Vẽ (A:AH), vẽ HI vuông góc với AC, HI cắt (A) tại M. Chứng minh: CM là tiếp tuyến của (A)

c) Vẽ đường kính MG của (A). Chứng minh BG là tiếp tuyến của (A)

Lời giải:

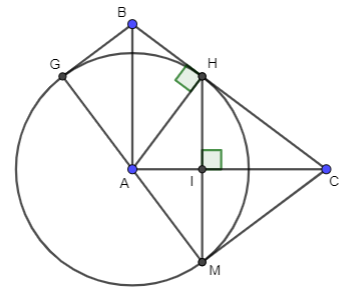
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) (ảnh 17)

a) Áp dụng định lí Pytago vào vuông tại A, ta được:

$B C^{2} = A B^{2} + A C^{2} \Leftrightarrow B C^{2} = 3^{2} + 4^{2} = 25$

hay BC = 5(cm)

Xét $Δ A B C$ vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

$A H \cdot B C = A B \cdot A C \Leftrightarrow A H \cdot 5 = 3 \cdot 4 = 12$

hay AH = 2,4(cm)

Vậy: BC = 5cm; AH = 2,4cm

b) Xét (A) có

AI là một phần đường kính

MH là dây

$A I ⊥ M H$ tại I(gt)

Do đó: I là trung điểm của MH(Định lí đường kính vuông góc với dây)

Xét $Δ C M I$ vuông tại I và $Δ C H I$ vuông tại I có

CI chung

IM = IH(I là trung điểm của MH)

Do đó: $Δ C M I = Δ C H I$ (hai cạnh góc vuông)

Suy ra: CM = CH(hai cạnh tương ứng)

Xét $Δ C M A$ và $Δ C H A$ có

CM = CH(cmt)

CA chung

AM = AH( = R)

Do đó: $Δ C M A = Δ C H A (c - c - c)$

Suy ra: $\hat{C M A} = \hat{C H A}$ (Hai góc tương ứng)

mà $\hat{C H A} = 90^{0}$ (gt)

nên $\hat{C M A} = 90^{0}$

hay CM là tiếp tuyến của (A)

Bài 38: Có bao nhiêu số tự nhiên lẻ có 4 chữ số khác nhau?

A. 2240

B. 2520

C. 2016

D. 256

Lời giải:

Gọi số cần tìm là: $\bar{a b c d}$

Vì số cần tìm là số lẻ nên: $d \in \{1; 3; 5; 7; 9\}$ → d có 5 cách

$a \neq d,0 \to$ a có 8 cách

$b \neq d \neq a \to$ b có 8 cách

$c \neq a \neq b \neq d \to$ c có 7 cách

Vậy có tất cả $5.8.8.7 = 2240$ số.

Đáp án A

Bài 39: Có bao nhiêu số tự nhiên có bốn chữ số đôi một khác nhau?

A. 4536

B. 6543

C. 3546

D. 6345

Lời giải:

số đầu tiên có 9 cách chọn trong các số từ 1 đến 9.

Chọn 3 chữ số trong 9 chữ số còn lại là $A_{9}^{3}$

Vậy có $9. A_{9}^{3} = 4536$ số.

Bài 40: Tìm số hạng thứ 7 trong khai triển ${(x + 2)}^{10}$

Lời giải:

Số hạng tổng quát trong khai triển ${(x + 2)}^{10}$ có dạng:

$_{k = 0}^{10} C_{10}^{k} 2^{k} . x^{10 - k} (0 \leq k \leq 10; k \in ℕ)$

Số hạng thứ 7 là: $C_{10}^{6} {.2}^{6} . x^{4} = 13440 x^{4}$

Bài 41: Tìm số hạng thứ năm trong khai triển ${(x + \frac{2}{x})}^{10}$ mà trong khai triển đó số mũ của x giảm dần.

Lời giải:

Số hạng thứ trong khai triển là

$t_{k + 1} = C_{10}^{k} x^{10 - k} {(\frac{2}{x})}^{k}$

Vậy $t_{5} = C_{10}^{4} x^{10 - 4} . {(\frac{2}{x})}^{4} = 210. x^{6} . \frac{16}{x^{4}} = 3360 x^{2}$

$t_{5} = 3360 x^{2}$

Bài 42: Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp 12A, 3 học sinh lớp 12B và 5 học sinh lớp 12C thành một hàng ngang. Xác suất để trong 10 học sinh trên không có 2 học sinh cùng lớp đứng cạnh nhau bằng

A. 11 630

B. 1 126

C. 1 105

D. 1 42

Lời giải:

Coi 5 bạn của cả 12A và B vào một lớp 12X nào đó. Do số lượng ở đề nên ta có hai trường hợp

TH1. Các bạn 12C và 12X xen kẽ nhau. Có $5! .5! .2 = 28800$ cách

TH2. Có hai bạn lớp 12A và 12B dính với nhau. Ta có như 12X chỉ có 4 bạn. rồi lại làm xen kẽ. Chọn 2 bạn dính nhau

và hoán vị 2 bạn đó có 12 cách, 5 bạn 12C tạo ra 4 khe để 4 bạn của lớp 12X đứng vào nên có tất cả là

$12.5! .4! = 34560$

Đáp án cần chọn là A

Bài 43: Một nhóm gồm 10 học sinh trong đó có 4 nữ và 6 nam. Hỏi có bao nhiêu cách xếp 10 học sinh trên thành 1 hàng dọc sao cho 4 học sinh nữ phải đứng liền nhau?

Lời giải:

Số cách xếp 4 bạn nữ đứng cạnh nhau : 4! (cách)

Số cách xếp 6 bạn nam đứng cạnh nhau : 6!(cách)

Đổi chỗ nam và nữ có : 2 (cách)

→ Số cách xếp : $2.4! .6!$ (cách)

Bài 44: Có 6 học sinh nam và 2 học sinh nữ được xếp thành một hàng ngang. Hỏi có bao nhiêu cách xếp sao cho hai học sinh nữ không đứng cạnh nhau?

A. 30240

B. 30420

C. 34020

D. 32400

Lời giải:

Trường hợp 1: ta xếp 8 học sinh đứng tùy ý thành hàng ngang, có 8!(cách xếp).

Trường hợp 2: ta xếp 8 học sinh sao cho 2 nữ đứng cạnh nhau, coi 2 nữ là 1 nhóm.

+) Xếp 6 nam và nhóm nữ, có 7! (cách xếp)

+) Xếp 2 nữ trong nhóm: có 2! (cách xếp)

Vậy có 7!.2! (cách xếp).

Số cách xếp sao cho hai học sinh nữ không đứng cạnh nhau: $8! - 7! 2! = 30240$ (cách xếp)

Chọn A

Bài 45: Một cái bể bơm có thể bơm đầy 1 cái bể trong 6 giờ . máy thứ hai bơm đầy bể mất $\frac{2}{3}$ số giờ đó, máy thứ ba bơm đầy bể mất $\frac{1}{2}$ số giờ mà máy thứ hai bơm đầy bể. Hỏi nếu mở đồng loạt cả ba máy cùng 1 múc thì bao lâu bể đầy.

Lời giải:

Máy bơm thứ nhất có thể bơm đầy 1 cái bể trong 6 giờ :

Vậy 1 giờ máy thứ nhất bơm được $\frac{1}{6}$ bể

Máy thứ hai bơm đầy bể mất $\frac{2}{3}$ số giờ đó , → 4 giờ: Vậy 1 giờ máy thứ hai bơm được $\frac{1}{4}$ bể

Máy thứ ba bơm đầy bể mất 1/2 số giờ mà máy thứ hai bơm đầy bể, → 2 giờ:

Vậy 1 giờ máy thứ ba bơm được $\frac{1}{2}$ bể

Vậy trong 1 giờ cả 3 vòi chảy được: $\frac{1}{6} + \frac{1}{4} + \frac{1}{2} = \frac{11}{12}$ (bể)

Thời gian để chảy đầy bể là : $1 : \frac{11}{12} = \frac{12}{11}$ (giờ)

ĐS: $\frac{12}{11}$ giờ

Bài 46: Hai máy bơm cùng làm việc thì sau 12 giờ bơm nước đầy bể, nếu máy bơm thứ nhất làm 3 giờ và máy bơm thứ hai làm 18 giờ thì hai máy cũng bơm nước đầy bể. hỏi nếu làm một mình thì mỗi máy bơm đầy bể trong bao lâu?

Lời giải:

Giải thích các bước giải:

Gọi a là số giờvòi 1 chảy 1 mình làm đầy bể. Vậy mỗi giờ chảy được $\frac{1}{a}$ bể

Gọi b là số giờ vòi 2 chảy 1 mình làm đầy bể.1 giờ chảy: $\frac{1}{b}$ bể.

Ta có : $\frac{1}{a} + \frac{1}{b} = \frac{1}{12} \to \frac{3}{a} + \frac{3}{b} = \frac{1}{4}$ (1)

và $\frac{3}{a} + \frac{18}{b} = 1$ (2)

Lấy (2) - (1): $\frac{15}{b} = \frac{3}{4} \Rightarrow \frac{1}{b} = \frac{3}{60} = \frac{1}{20} \Rightarrow$ vòi 2 chảy đầy bể trong 20 giờ.

và $\frac{1}{a} + \frac{1}{20} = \frac{1}{12}$ thì: $\frac{1}{a} = \frac{1}{12} - \frac{1}{20} = \frac{2}{60} = \frac{1}{30}$ . Vòi 1 chảy 30 giờ thì đầy bể.

Bài 47: Cho đường thẳng d: $y = (2 m + 1) . x - 2$ và m khác $\frac{1}{2}$ giả sử d cắt ox tại a cắt oy tại b tìm m để diện tích tam giác oab bằng $\frac{1}{2}$

Lời giải:

$x = 0 \Rightarrow y = - 2 \Rightarrow O B = 2 y = 0 \Rightarrow x = \frac{2}{2 m + 1} \Rightarrow O A = |\frac{2}{2 m + 1}| \Leftrightarrow |2 m + 1| = 4 \Leftrightarrow [\begin{matrix} 2 m + 1 = 4 \\ 2 m + 1 = - 4 \end{matrix} \Leftrightarrow [\begin{matrix} m = \frac{3}{2} \\ m = - \frac{5}{2} \end{matrix}$

Bài 48: Cho $2^{n} + 1$ là số nguyên tố (n > 2)

Chứng minh $2^{n} - 1$ là hợp số

Lời giải:

Ta có: $2^{n} + 1; 2^{n}; 2^{n} - 1$ là 3 số tự nhiên liên tiếp

→ một trong 3 số trên chia hết cho 3

mà $2^{n} + 1$ là số nguyên tố (n > 2) $\to 2^{n} + 1$ không chia hết cho 3

Mặt khác: $2^{n}$ không chia hết cho 3

$\to 2^{n} - 1$ chia hết cho 3

Bài 49: Cho $2^{n} - 1$ là số nguyên tố. Chứng minh n cũng là số nguyên tố.

Lời giải:

Giải thích các bước giải:

Giả sử n là hợp số $\to n = p . q (p, q \in N; p, q > 1)$

Khi đó $2^{n} - 1 = 2^{p} q - 1 = {(2^{p})}^{q} - 1 = (2^{p} - 1) {(2^{p})}^{q} - 1 + {(2^{p})}^{q} - 2 + ... + 1)$

Vì $p > 1 \Rightarrow 2^{p} - 1 > 1$ và ${(2^{p})}^{q} - 1 = {(2^{p})}^{q} - 2 + ... + 1 > 1$
Dẫn đến $2^{n} - 1$ là hợp số: trái với giả thiết $2^{n} - 1$ là số nguyên tố

Vậy n là số nguyên tố (đpcm)

Bài 50: Số 0 và số 1 có phải số chính phương không?

Lời giải:

O là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 0 = 0

1 là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 1 = 1

Bài 51: Tứ giác ABCD có $\hat{A} : \hat{B} : \hat{C} : \hat{D}$ tỉ lệ với 3 : 4 : 5 : 6

a) Tính các góc của tứ giác

b) Tứ giác ABCD là hình gì ? Vì sao?

Lời giải:

a) Do tổng 4 góc của 1 tứ giác bằng 360⁰ nên:

$\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360^{0}$

Mà $\hat{A} : \hat{B} : \hat{C} : \hat{D} = 3 : 4 : 5 : 6$

$\Rightarrow \frac{\hat{A}}{3} = \frac{\hat{B}}{4} = \hat{\frac{C}{5}} = \frac{\hat{D}}{6} = \frac{\hat{A} + \hat{B} + \hat{C} + \hat{D}}{3 + 4 + 5 + 6} = \frac{360^{0}}{18} = 20^{0}$

$\Rightarrow \{\begin{matrix} \hat{A} = {3.20}^{0} = 60^{0} \\ \hat{B} = {4.20}^{0} = 80^{0} \\ \hat{C} = {5.20}^{0} = 100^{0} \\ \hat{D} = {6.20}^{0} = 120^{0} \end{matrix}$