Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho tam giác ABC vuông tại A có AB = 3cm; AC = 4cm, đường cao AH.
Bài 37: Cho tam giác ABC vuông tại A có AB = 3cm; AC = 4cm, đường cao AH.
a) Tính BC,AH;
b) Vẽ (A:AH), vẽ HI vuông góc với AC, HI cắt (A) tại M. Chứng minh: CM là tiếp tuyến của (A)
c) Vẽ đường kính MG của (A). Chứng minh BG là tiếp tuyến của (A)
Lời giải:
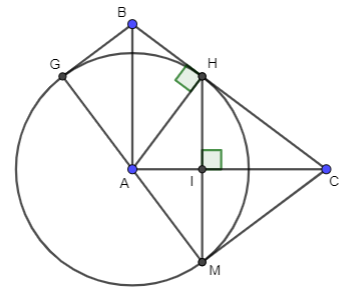
a) Áp dụng định lí Pytago vào vuông tại A, ta được:
hay BC = 5(cm)
Xét vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
hay AH = 2,4(cm)
Vậy: BC = 5cm; AH = 2,4cm
b) Xét (A) có
AI là một phần đường kính
MH là dây
tại I(gt)
Do đó: I là trung điểm của MH(Định lí đường kính vuông góc với dây)
Xét vuông tại I và vuông tại I có
CI chung
IM = IH(I là trung điểm của MH)
Do đó: (hai cạnh góc vuông)
Suy ra: CM = CH(hai cạnh tương ứng)
Xét và có
CM = CH(cmt)
CA chung
AM = AH( = R)
Do đó:
Suy ra: (Hai góc tương ứng)
mà (gt)
nên
hay CM là tiếp tuyến của (A)
Bài viết cùng bài học:




