Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 31)

Ngọc Nguyễn Ngày: 13-06-2023 Tổng hợp kiến thức

382

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 31) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 31)

Câu 1: Năm ngoái, tổng số dân của hai tỉnh A và B là 4 triệu. Năm nay, dân số của tỉnh A tăng thêm 1,1%, còn dân số của tỉnh B tăng thêm 1,2%. Tuy vậy số dân của tỉnh A năm nay vẫn nhiều hơn tỉnh B là 807 200 người. Tính số dân năm ngoái của mỗi tỉnh.

Lời giải:

* Phân tích:

	Năm ngoái	Năm nay
Tỉnh A	x	x + x.1,1% = 1,011.x
Tỉnh B	4 – x	(4 – x) + (4 – x).1,2% = (4 – x).1,012

Dân số tỉnh A năm nay nhiều hơn dân số tỉnh B là 807 200 người = 0,8072 (triệu người) nên ta có phương trình:

1,011.x – 1,012.(4 – x) = 0,8072.

* Giải:

Gọi x là số dân năm ngoái của tỉnh A (0 < x < 4; x ∈ ℕ*; triệu người)

Số dân năm ngoái của tỉnh B là 4 – x (triệu người).

Năm nay dân số của tỉnh A tăng 1,1% nên số dân của tỉnh A năm nay là:

x + 1,1% x = 1,011.x (triệu người).

Năm nay dân số của tỉnh B tăng 1,2 % nên số dân của tỉnh B năm nay là:

(4 – x) + 1,2% (4 – x) = 1,012(4 – x) (triệu người).

Vì số dân tỉnh A năm nay hơn tỉnh B là 807 200 người = 0,8072 triệu người nên ta có phương trình:

1,011.x – 1,012(4 – x) = 0,8072

⇔ 1,011x – 4,048 + 1,012x = 0,8072

⇔ 2,023. x = 4,8552

⇔ x = 2,4 (thỏa mãn).

Vậy dân số của tỉnh A năm ngoái là 2,4 triệu người, dân số tỉnh B năm ngoái là 4 – 2,4 = 1,6 triệu người.

Câu 2: Phân tích đa thức thành nhân tử:

a) x² – xy + 2x – 2y.

b) x² + 10xy – 25 + 25y².

Lời giải:

a) x² – xy + 2x – 2y

= x(x – y) + 2 (x – y)

= (x – y)(x + 2).

b) x² + 10xy – 25 + 25y²

= (x² + 10xy + 25y²) – 25

= (x + 5y)² – 25

= (x + 5y + 5)(x + 5y – 5).

Câu 3: Tìm số tự nhiên có 3 chữ số biết rằng nếu xóa chữ số 2 ở hàng trăm của số đó thì được số mới bằng $\frac{1}{9}$ số đó.

Lời giải:

Nếu xóa chữ số 2 ở hàng phần trăm đi ta được số mới kém số đầu 200 đơn vị.

Số mới bằng $\frac{1}{9}$ số ban đầu thì nếu số mới là 1 phần thì số cũ là 9 phần và hơn kém nhau 200 đơn vị.

Vậy số ban đầu là: 200 : (9 – 1) × 9 = 225.

Câu 4: Tìm số nguyên x, y biết xy – 2x – 3y = 1.

Lời giải:

Ta có: xy – 2x + 3y = 1.

(xy − 2x) + (3y − 6) = −5

x(y − 2) + 3(y − 2) = −5

(x + 3)(y − 2) = −5 = 1.(−5) = (−1).5

Vì x, y là số nguyên nên x + 3 và y – 2 cũng là số nguyên.

Do đó ta có bảng sau:

x + 3	1	–5	5	–1
y – 2	–5	1	–1	5
x	–2	–8	2	–4
y	–3	3	1	7

Vậy (x; y) ∈ {(−2; −3); (−8; 3); (2; 1); (−4; 7)}.

Câu 5: Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số: y = 4sin²x – 4sinx + 3.

Lời giải:

Tập xác định: D = ℝ.

y = 4sin²x – 4sinx + 3

= 4sin²x – 4sinx + 1 + 2

= (2sinx – 1)² + 2.

Ta có: –1 ≤ sinx ≤ 1

⇔ –2 ≤ 2sinx ≤ 2

⇔ –3 ≤ 2sinx – 1 ≤ 1

⇔ 0 ≤ (2sinx – 1)² ≤ 1

⇔ 2 ≤ (2sinx – 1)² + 2 ≤ 3

⇔ 2 ≤ y ≤ 3

Câu 6: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: y = 4sin²x – 4sinx + 1.

Lời giải:

Tập xác định: D = ℝ.

y = 4sin²x – 4sinx + 1

= (2sinx – 1)².

Ta có: –1 ≤ sinx ≤ 1

⇔ –2 ≤ 2sinx ≤ 2

⇔ –3 ≤ 2sinx – 1 ≤ 1

⇔ 0 ≤ (2sinx – 1)² ≤ 1

⇔ 0 ≤ y ≤ 1

Khi đó giá trị nhỏ nhất của y là 0, xảy ra khi và chỉ khi (2sinx – 1)² = 0

$\Leftrightarrow \sin x = \frac{1}{2} \Leftrightarrow [\begin{array}{l} x = \frac{π}{6} + k 2 π \\ x = \frac{5 π}{6} + k 2 π \end{array}$

Khi đó giá trị lớn nhất của y là 1, xảy ra khi và chỉ khi sinx = 1 $\Leftrightarrow x = \frac{π}{2} + k 2 π$ .

Câu 7: Giải phương trình: cos²x + 3cosx = 0.

Lời giải:

cos²x + 3cosx = 0

⇔ cosx(cosx + 3) = 0

$\Leftrightarrow [\begin{array}{l} \cos x = 0 \\ \cos x = - 3 (l o a i) \end{array} \Leftrightarrow x = \frac{π}{2} + k π, k \in ℤ$

Vậy phương trình trên có nghiệm là $x = \frac{π}{2} + k π, k \in ℤ$ .

Câu 8: Tính tổng của các số nguyên x thỏa mãn $- 2009 < x \leq 2008$ .

Lời giải:

Ta có: $- 2009 < x \leq 2008$ và x là số nguyên nên ta có:

x ∈ {–2008; –2007; …; –1; 0 ; 1; …; 2007; 2008}.

Khi đó tổng của các số nguyên x thỏa mãn $- 2009 < x \leq 2008$ là:

–2008 + (–2007) + …+ (–1) + 0 + 1 + … + 2007 + 2008

= [(–2008) + 2008] + [(–2007) + 2007] + …+ [(–1) + 1] + 0

= 0.

Câu 9: sin15° bằng bao nhiêu?

Lời giải:

Dùng máy tính cầm tay, ta bấm lần lượt các nút $\sin 1 5 °''' =$ được kết quả hiện trên màn hình máy tính như sau:

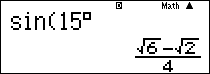
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 31) (ảnh 1)

Vậy $\sin 15 ° = \frac{\sqrt{6} - \sqrt{2}}{4}$ .

Câu 10: Trong khai triển nhị thức (3 + 0,02)⁷. Tìm tổng của ba số hạng đầu tiên.

A. 2289,3283;

B. 2291,1012;

C. 2275,93801;

D. 2291,1141.

Lời giải:

Ta có: (3 + 0,02)⁷ = $C_{7}^{0} {.3}^{7} + C_{7}^{1} {.3}^{6} .0,02 + C_{7}^{2} {.3}^{5} . {(0,02)}^{2} + ...$

Tổng ba số hạng đầu tiên là:

$C_{7}^{0} {.3}^{7} + C_{7}^{1} {.3}^{6} .0,02 + C_{7}^{2} {.3}^{5} . {(0,02)}^{2} = 2291,1012$ .

Câu 11: Cho hình thang ABCD có đáy AB, DC. Gọi M, N lần lượt là trung điểm AD và BC. Chứng minh MN // DC và $M N = \frac{1}{2} (A B + D C)$ .

Lời giải:

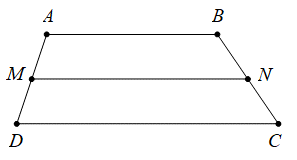
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 31) (ảnh 2)

Ta có: MA = MB (Vì M là trung điểm của AD);

NB = NC (Vì N là trung điểm của BC)

Suy ra MN là đường trung bình của hình thang ABCD với AB // CD.

$\Rightarrow M N = \frac{1}{2} (A B + D C)$ và MN // AB // CD.

Câu 12: Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC.

a) Chứng minh hai tam giác ABM và ACM bằng nhau.

b) Chứng minh AM vuông góc với BC.

c) Chứng minh AM là phân giác của góc A.

Lời giải:

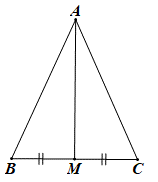
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 31) (ảnh 3)

a) Xét ΔABM và ΔACM ta có:

AB = AC (theo giả thiết);

AM chung;

MB = MC (do M là trung điểm của BC)

Suy ra ΔABM = ΔACM (c.c.c).

b) Từ ΔABM = ΔACM suy ra $\hat{B M A} = \hat{C M A}$ (hai góc tương ứng).

Mà $\hat{B M A} + \hat{C M A} = 180 °$ nên suy ra $\hat{B M A} = \hat{C M A} = 90 °$ .

Suy ra AM vuông góc với CB.

c) Từ ΔABM = ΔACM suy ra $\hat{B A M} = \hat{C A M}$ suy ra AM là tia phân giác của góc A.

Câu 13: Có bao nhiêu phân số với mẫu số có 2 chữ số tương đương với $\frac{1}{5}$ ?

Lời giải:

Mẫu số bé nhất có hai chữ số mà chia hết cho 5 là 10.

Mẫu số lớn nhất có hai chữ số mà chia hết cho 5 là 95.

Vậy có số các phân số bằng $\frac{1}{5}$ có mẫu số là số có 2 chữ số là (95 – 10) : 5 + 1 = 18.

Câu 14: Diện tích hình bình hành bằng 24 cm². Khoảng cách từ giao điểm hai đường chéo đến các cạnh hình bình hành bằng 2 cm và 3 cm. Tính chu vi của hình bình hành.

Lời giải:

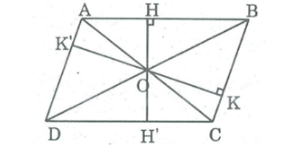
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 31) (ảnh 4)

Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, khoảng cách từ O đến cạnh AB là OH = 2cm , đến cạnh BC là OK = 3 cm.

* Kéo dài OH cắt cạnh CD tại H'.

Ta có OH ⊥ BC

⇒ OH' ⊥ CD và OH' = 2cm

Suy ra HH' bằng đường cao của hình bình hành.

$S_{A B C D} = H H^{'} . A B \Leftrightarrow A B = \frac{S_{A B C D}}{H H^{'}} = \frac{24}{4} = 6 (c m)$

* Kéo dài OK cắt AD tại K'.

Ta có: OK ⊥ BC ⇒ OK' ⊥ CD và OK' = 3 (cm)

Suy ra KK' là đường cao của hình bình hành.

$S_{A B C D} = K K^{'} . B C \Rightarrow B C = \frac{S_{A B C D}}{K K^{'}} = \frac{24}{6} = 4 (c m)$

Chu vi của hình bình hành ABCD là (6 + 4).2 = 20 (cm).

Câu 15: Cho hàm số y = (2 – m)x + 3.

a) Tìm m để (d) đi qua điểm A(2; 3).

b) Tìm m để (d) cắt trục hoành tại điểm có hoành độ là –1.

c) Tìm m để (d) cắt trục tung tại điểm có tung độ là 3.

Lời giải:

a) Để (d) đi qua điểm A(2; 3) thì:

3 = (2 – m).2 + 3 ⇔ 2.(2 – m) = 0 ⇔ m = 2.

Vậy m = 2 là giá trị cần tìm.

b) Để (d) cắt trục hoành thì 2 – m ≠ 0 ⇔ m ≠ 2.

Do (d) cắt trục hoành tại điểm có hoành độ là –1 nên tọa độ giao điểm đó là A(–1; 0).

Do điểm A thuộc (d) nên ta có:

0 = (2 – m).(–1) + 3 ⇔ m – 2 = –3 ⇔ m = –1 (tm).

Vậy m = –1 là giá trị cần tìm.

c) Do (d) cắt trục tung tại điểm có tung độ là 3 nên tọa độ giao điểm đó là B(0; 3).

Do điểm B thuộc (d) nên ta có:

3 = (2 – m).0 + 3 ⇔ 0.(2 – m) = 0 (luôn đúng với mọi m).

Vậy với mọi giá trị m ∈ ℝ thì (d) cắt trục tung tại điểm có tung độ là 3.

Câu 16: Cho hàm số y = (a – 2)x + 5 có đồ thị là đường thẳng d. Tìm a để đường thẳng d đi qua điểm M(2; 3).

A. a = –1;

B. a = 0;

C. a = –2;

D. a = 1.

Lời giải:

Đáp án đúng là: D

Để đường thẳng (d) đi qua điểm M(2; 3) thì:

3 = (a – 2).2 + 5 ⇔ 2.(a – 2) = –2 ⇔ a – 2 = –1 ⇔ a = 1.

Câu 17: Một chiếc cổng hình parabol dạng $y = - \frac{1}{2} x^{2}$ có chiều rộng d = 8 m. Hãy tính chiều cao h của cổng (Xem hình minh họa bên cạnh).

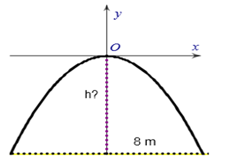
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 31) (ảnh 5)

A. h = 8 m;

B. h = 7 m;

C. h = 5 m;

D. h = 9 m.

Lời giải:

Đáp án đúng là: A

Đường thẳng chứa chiều rộng d = 8m cắt (P) tại A(4; –h)

Điểm A ∈ (P) $\Rightarrow - h = - \frac{1}{2} {.4}^{2} \Rightarrow h = 8 (m)$ .

Câu 18: Cho hình chóp S.ABCD đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của SB, AB. Điểm M là một điểm bất kì trên nửa đường thẳng Ax chứa C. Biện luận theo vị trí của điểm M trên Ax các dạng của thiết diện của hình chóp cắt bởi mặt phẳng (IJM).

Lời giải:

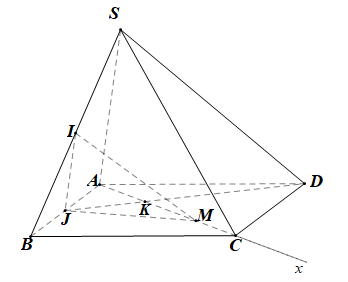
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 31) (ảnh 6)

Gọi K là giao điểm của AC và JD.

Khi đó:

• Nếu M ∈ Cx thì thiết diện là hình tam giác;

• Nếu M ∈ KC thì thiết diện là hình tứ giác;

• Nếu M ∈ Cx thì thiết diện là hình ngũ giác.

Câu 19: Cho đường thẳng (d): y = (m² – 3)x – m + 1. Tìm m để (d) cắt (d’): y = –2x tại điểm có hoành độ x = 2.

Lời giải:

Để (d) cắt (d’) thì m² – 3 ≠ –2 ⇔ m² ≠ 1 ⇔ m ≠ ± 1.

Phương trình hoành độ giao điểm của (d) và (d’) là:

(m² – 3)x – m + 1 = –2x

⇔ (m² – 1)x = m – 1

$\Leftrightarrow x = \frac{m - 1}{m^{2} - 1} = \frac{m - 1}{(m - 1) (m + 1)} = \frac{1}{m + 1}$

Để (d) cắt (d’) tại điểm có hoành độ x = 2 thì

$\frac{1}{m + 1} = - 2 \Rightarrow - 2 m - 2 = 1 \Leftrightarrow m = \frac{- 3}{2} (t m)$

Vậy $m = - \frac{3}{2}$ .

Câu 20: Mỗi giờ ô tô đi được 43,8km. Hỏi trong 5 giờ ô tô đi được số ki lô mét là bao nhiêu?

Lời giải:

5 giờ ôtô đi được số ki lô mét là:

43,8 × 5 = 219 (km)

Đáp số: 219 km.

Câu 21: Một mảnh đất hình thoi có tổng độ dài hai đường chéo là là 76,4m. Tính diện tích mảnh đất đó, biết đường chéo thứ nhất hơn đường chéo thứ 2 là 4,4m.

Lời giải:

Đường chéo lớn hơn có độ dài là: (76,4 + 4,4) : 2 = 40,4 (m).

Đường chéo nhỏ hơn có độ dài là: 40,4 – 4,4 = 36 (m).

Diện tích mảnh đất đó là: 40,4 . 36 : 2 = 727,2 (m²).

Câu 22: Trong một cuộc thi chạy, nếu bạn vượt qua người thứ 2, bạn sẽ đứng thứ mấy?

Lời giải:

Trong một cuộc thi chạy, nếu bạn vượt qua người thứ 2 thì bạn vẫn sau người đi đầu thứ nhất, nên bạn vẫn chỉ đứng thứ 2.

Câu 23: Để sửa một ngôi nhà cần một số thợ làm việc trong một thời gian quy định. Nếu giảm ba người thì thời gian kéo dài sáu ngày. Nếu tăng thêm hai người thì xong sớm hai ngày. Hỏi theo quy định cần bao nhiêu thợ và làm trong bao nhiêu ngày. Biết rằng khả năng lao động của mọi thợ đều như nhau?

Lời giải:

Gọi số thợ cần thiết là x (người), x ∈ ℕ* , thời gian cần thiết là y (ngày), y > 0.

Số ngày công cần để hoàn thành công việc là: xy (ngày).

Nếu giảm đi 3 người thì thời gian kéo dài 6 ngày. Như vậy, x – 3 người làm trong y + 6 ngày thì xong công việc. Do đó, ta có phương trình (x – 3)(y + 6) = xy.

Nếu tăng thêm 2 người thì xong sớm 2 ngày. Như vậy, x + 2 người làm trong y – 2 ngày thì xong công việc. Do đó, ta có phương trình: (x + 2)(y – 2) = xy.

Ta có hệ phương trình:

$\{\begin{cases} (x - 3) (y + 6) = x y \\ (x + 2) (y - 2) = x y \end{cases} \Leftrightarrow \{\begin{cases} x y + 6 x - 3 y - 18 = x y \\ x y - 2 x + 2 y - 4 = x y \end{cases} \Leftrightarrow \{\begin{cases} 6 x - 3 y = 18 \\ - 2 x + 2 y = 4 \end{cases} \Leftrightarrow \{\begin{cases} 2 x - y = 6 \\ x - y = - 2 \end{cases} \Leftrightarrow \{\begin{cases} x = 8 \\ y = x + 2 \end{cases} \Leftrightarrow \{\begin{cases} x = 8 \\ y = 10 \end{cases} (t m)$

Vậy cần 8 người làm trong 10 ngày thì xong công việc.

Câu 24: Một miếng đất hình chữ nhật có chiều dài 65,3m. Vì mở rộng đường quốc lộ nên miếng đất bị xén đi một góc có dạng hình tam giác (phần tô đậm của hình vẽ). Tính diện tích phần đất còn lại.

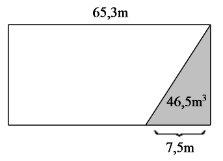
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 31) (ảnh 7)

Lời giải:

Chiều rộng của mảnh đất hình chữ nhật ban đầu là:

(2 . 46,5) : 7,5 = 12,4 (m).

Diện tích miếng đất hình chữ nhật ban đầu là:

65,3 . 12,4 = 809,72 (m²)

Vậy diện tích phần đất còn lại là:

809,72 – 46,5 = 763,22 (m²).

Đáp số: 763,22 m².

Câu 25: Lập bảng số nguyên tố nhỏ hơn 200.

Lời giải:

Bảng số nguyên tố nhỏ hơn 200 là:

2	3	5	7	11	13	17	19
23	29	31	37	41	43	47	53
59	61	67	71	73	79	83	89
97	101	103	107	109	113	127	131
137	139	149	151	157	163	167	173
179	181	191	193	197	199

Câu 26: Tìm 2 số chẵn có tổng bằng 216, biết giữa chúng có 5 số chẵn.

Lời giải:

Số khoảng cách là: 5 + 1 = 6 (khoảng cách)

Hiệu các số là: 2 × 6 = 12

Số bé là: (216 − 12) : 2 = 102

Số lớn là: 102 + 12 = 114

Vậy hai số cần tìm là 102 và 114.

Câu 27: Tìm số a, b biết: ab + a + b = 95.

Lời giải:

Ta có: ab + a + b = 95

Hay 10a + b + a + b = 95

11a + 2b = 95

$\bar{a a}$ + 2b = 95

Vì 95 là số lẻ và 2b là số chẵn nên $\bar{a a}$ là số lẻ

Ta có $\bar{a a}$ thuộc {11; 33; 55; 77; 99}.

Để b là số có 1 chữ số thì b × 2 cao nhất là: 9 × 2 = 18

Ta có: 95 − 11 = 84, 95 − 33 = 62, 95 − 55 = 40, 95 − 77 = 18, 95 − 99 = −5.

Trong các giá trị vừa tìm được thì chỉ có 95 − 77 mới không vượt qua 18 và là số tự nhiên.

Vậy a = 7 và b = 9.

Thử lại: 79 + 7 + 9 = 95

Câu 28: Tìm hai số biết a + b = 95 và a − b = 5

Lời giải:

Số lớn là:

a = (95 + 5) : 2 = 50

Số bé là:

b = (95 − 5) : 2 = 45

Vậy a = 50 và b = 45

Câu 29: Phân tích đa thức (x² + 4x − 3)² − 5x(x² + 4x − 3) + 6x² thành nhân tử.

Lời giải:

(x² + 4x − 3)² − 5x(x² + 4x − 3) + 6x²

= (x² + 4x − 3)² − 3x(x² + 4x − 3) − 2x(x² + 4x − 3) + 6x²

= (x² + 4x − 3)[(x² + 4x − 3) − 3x] − 2x[(x² + 4x − 3) − 3x]

= [(x² + 4x − 3) − 3x].[(x² + 4x − 3) − 2x]

= (x² + x − 3).(x² + 2x − 3)

= (x² + x − 3).(x² + x − 3x − 3)

= (x² + x − 3).[x(x + 1) − 3(x + 1)]

= (x² + x − 3).(x + 1).(x − 3)

Câu 30: Tìm tất cả các số tự nhiên n thõa mãn 5n + 14 chia hết cho n + 2.

Lời giải:

Ta có 5n + 14 ⋮ n + 2

5n + 10 + 4 ⋮ n + 2

5(n + 2) + 4 ⋮ n + 2

Vì 5(n + 2) ⋮ n + 2 nên để 5(n + 2) + 4 ⋮ n + 2 thì suy ra:

4 ⋮ n + 2 ⇔ n + 2 thuộc Ư(4) = {1; 2; 4; −1; −2; −4}

⇔ n thuộc {−1; 0; 2; −3; −4; −6}

Vậy các số tự nhiên n thỏa mãn là n thuộc {0; 2}.

Câu 31: Tìm hai số biết tổng của hai số đó bằng 35,36; hiệu của hai số đó bằng 18,64.

Lời giải:

Số lớn là: (35,36 + 18,64) : 2 = 27

Số bé là: 35,36 − 27 = 8,36

Đáp số: Số lớn: 27; số bé: 8,36.

Câu 32: Một mảnh đất hình chữ nhật có chu vi gấp 8 lần chiều rộng. Chiều dài hơn chiều rộng 20 m. Tính diện tích mảnh đất đó.

Lời giải:

Gọi a là chiều dài và b là chiều rộng.

Theo đề bài ta có:

$\{\begin{cases} P = (a + b) . 2 (1) \\ P = 8 b (2) \\ a = b + 20 (3) \end{cases}$

Xét điều kiện (1) và (2), ta có:

(a + b).2 = 8b

⇔ 2a + 2b = 8b

⇔ 2a = 6b

⇔ a = 3b

Xét thêm điều kiện (3) ta có:

2.(b + 20) = 6b

⇔ 2b + 40 = 6b

⇔ 40 = 4b

⇔ b = 10

Từ đây suy ra: a = b + 20

⇔ a = 10 + 20 = 30

Vậy diện tích mảnh đất đó là:

S = a.b = 30.10 = 300 (m²)

Đáp số: 300 m².

Câu 33: Một mảnh đất hình chữ nhật có chu vi gấp 8 lần chiều rộng. Chiều dài hơn chiều rộng 20 m. Tính diện tích mảnh đất đó.

Lời giải:

Gọi a là chiều dài và b là chiều rộng.

Theo đề bài ta có:

$\{\begin{cases} P = (a + b) . 2 (1) \\ P = 8 b (2) \\ a = b + 36 (3) \end{cases}$

Xét điều kiện (1) và (2), ta có:

(a + b).2 = 8b

⇔ 2a + 2b = 8b

⇔ 2a = 6b

⇔ a = 3b

Xét thêm điều kiện (3) ta có:

2.(b + 36) = 6b

⇔ 2b + 72 = 6b

⇔ 72 = 4b

⇔ b = 18

Từ đây suy ra: a = b + 36

⇔ a = 18 + 36 = 54

Vậy diện tích mảnh đất đó là:

S = a.b = 54.18 = 972 (m²)

Đáp số: 972 m²

Câu 34: Tìm chữ số tận cùng của: 74³⁰.

Lời giải:

Ta có: 74³⁰ = 74.74.74.74…74.74 (Tích của 30 thừa số 74)

= (74.74).(74.74)…(74.74)

Do 74.74 = 5476 có chữ số tận cùng là 6

Nên 74³⁰ được phân tích thành tích của 15 thừa số 5476 có tận cùng là 6.

Vậy 74³⁰ có tận cùng là 6.

Câu 35: Tìm chữ số tận cùng của các số sau: 74³⁰; 49³¹; 97³²; 58³³; 22³⁵.

Lời giải:

+) $74^{30} = {(74^{2})}^{15} = {(\bar{.....6})}^{15} = \bar{.....6}$

Vậy 74³⁰ có chữ số tận cùng là 6.

+) $49^{31} = 49^{30} . 49 = {(49^{2})}^{15} . 49 = {(\bar{....1})}^{15} . 49 = \bar{....1} . \bar{....9} = \bar{....9}$

Vậy 49³¹ có chữ số tận cùng là 9.

+) $97^{32} = {(97^{4})}^{8} = {\bar{....1}}^{8} = \bar{....1}$

Vậy 97³² có chữ số tận cùng là 1.

+) $58^{33} = (58^{32}) . 58 = {(58^{4})}^{8} . 58 = {\bar{....6}}^{8} . \bar{....8} = \bar{....6} . \bar{....8} = \bar{....8}$

Vậy 58³³ có chữ số tận cùng là 8.

+) $23^{35} = 23^{32} . 23^{3} = {(23^{4})}^{8} . 23^{3} = {\bar{....1}}^{8} . \bar{....7} = \bar{....1} . \bar{....7} = \bar{....7}$

Vậy 22³⁵ có chữ số tận cùng là 7.

Câu 36: Tìm x, y, z thỏa mãn:

x² + y² + 2z² + xy + 2yz + 2zx + x + y + 1 = 0.

Lời giải:

x² + y² + 2z² + xy + 2yz + 2zx + x + y + 1 = 0

⇔ 2.(x² + y² + 2z² + xy + 2yz + 2zx + x + y + 1) = 0

⇔ 2x² + 2y² + 4z² + 2xy + 4yz + 4zx + 2x + 2y + 2 = 0

⇔ (x² + 2xy + y²) + 4z.(x + y) + 4z² + (x² + 2x + 1) + (y² + 2y + 1) = 0

⇔ (x + y)² + 4z.(x + y) + 4z² + (x + 1)² + (y + 1)² = 0

⇔ (x + y + 2z)² + (x + 1)² + (y + 1)² = 0

Mà (x + y + 2z)² ≥ 0; (x + 1)² ≥ 0; (y + 1)² ≥ 0 nên suy ra:

$\{\begin{cases} x + y + 2 z = 0 \\ x + 1 = 0 \\ y + 1 = 0 \end{cases} \Leftrightarrow \{\begin{cases} z = - \frac{x + y}{2} \\ x = - 1 \\ y = - 1 \end{cases} \Leftrightarrow \{\begin{cases} x = - 1 \\ y = - 1 \\ z = 1 \end{cases}$

Vậy (x; y; z) = (−1; −1; 1) là nghiệm của phương trình.

Câu 37: Hai ông cháu hiện nay có tổng số tuổi là 68. Biết rằng cách đây 5 năm cháu kém ông 52 tuổi. Tính tuổi mỗi người hiện nay.

Lời giải:

Cách đây 5 năm tổng tuổi 2 ông cháu là:

68 − (5 +5) = 58 (tuổi)

Cách đây 5 năm, tuổi cháu là:

(58 − 52) : 2 = 3 (tuổi)

Tuổi cháu hiện nay là:

3 + 5 = 8 (tuổi)

Tuổi ông hiện nay là:

68 − 8 = 60 (tuổi)

Đáp số: cháu: 8 tuổi; ông: 60 tuổi.

Câu 38: 105 cm² = ……… dm² = ……… m²

Lời giải:

105 cm² = 1,05 dm² = 0,0105 m²

Câu 39: Tính A = 1.2 + 2.3 + 3.4 + ... + n(n + 1).

Lời giải:

A = 1.2 + 2.3 + 3.4 + ... + n(n + 1)

3A = 1.2.3 + 2.3.3 + 3.4.3 + … + n(n + 1).3

3A = 1.2.(3 − 0) + 2.3.(4 − 1) + 3.4.(5 − 2) + … + n(n + 1)[(n + 2) − (n + 1)]

3A = 1.2.3 + 2.3.4 − 1.2.3 + 3.4.5 − 2.3.4 + … + n(n + 1)(n + 2) − (n − 1)n(n + 1)

3A = n(n + 1)(n + 2)

Vậy $A = \frac{n (n + 1) (n + 2)}{3}$ .

Câu 40: Tính giá trị của T biết: T = 2 + 3 + 4 + 5 + … + 2 015.

Lời giải:

Dãy số trên có số số hạng là:

(2 015 − 1) : 2 + 1 = 1 008

Giá trị của T là:

(2 015 + 2) × 1 008 : 2 = 1 016 568

Đáp số: 1 016 568.

Câu 41: Mua 15 quyển vở hết 36 000 đồng. Hỏi mua 25 quyển vở như thế hết bao nhiêu tiền?

Lời giải:

1 quyển hết số tiền là:

36 000 : 15 = 2 400 (đồng)

25 quyển vở hết số tiền là:

2 400 × 25 = 60 000 (đồng)

Đáp số: 60 000 đồng.

Câu 42: Cho A = {x thuộc ℤ | x < 4};

B = {x thuộc ℤ | (5x − 3x²)(x² + 2x − 3) = 0}.

a) Liệt kê các phần tử của hai tập hợp A và B.

b) Hãy các định các tập hợp A ∩ B, A ∪ B và A \ B.

Lời giải:

a) Tập hợp A gồm các số nguyên thỏa mãn nhỏ hơn 4.

Do đó A = {…; −3; −2; −1; 0; 1; 2; 3}.

Ta có: (5x − 3x²)(x² + 2x − 3) = 0

$\Rightarrow [\begin{array}{l} 5 x - 3 x^{2} = 0 \\ x^{2} + 2 x - 3 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 \\ x = \frac{5}{3} \\ x = 1 \\ x = - 3 \end{array}$

Mà x thuộc ℤ nên x thuộc {−3; 0; 1}

Suy ra B = {−3; 0; 1}.

b) Ta có:

A ∩ B = {−3; 0; 1} = B;

A ∪ B = {…; −3; −2; −1; 0; 1; 2; 3} = A;

A \ B = {…; −4; −2; −1; 2; 3}.

Câu 43: Nêu dấu hiệu chia hết cho 13

Lời giải:

Dấu hiệu chia hết cho 13: Tổng của số tạo bởi các chữ số đứng trước số tận cùng với 4 lần chữ số tận cùng chia hết cho 13.

Câu 44: Dấu hiệu chia hết cho 13 và 11 là gì?

Lời giải:

• Dấu hiệu chia hết cho 11: Hiệu của tổng các chữ số hàng chẵn với tổng các chữ số hàng lẻ chia hết cho 11.

• Dấu hiệu chia hết cho 13: Tổng của số tạo bởi các chữ số đứng trước số tận cùng với 4 lần chữ số tận cùng chia hết cho 13.

Câu 45: Chứng minh rằng: ƯCLN(a, b) = ƯCLN(5a + 2b, 7a + 3b).

Lời giải:

Gọi d là ước chung lớn nhất của 5a + 2b và 7a + 3b nên suy ra:

$\{\begin{cases} 5 a + 2 b ⋮ d \\ 7 a + 3 b ⋮ d \end{cases} \Rightarrow \{\begin{cases} 5 (7 a + 3 b) - 7 (5 a + 2 b) ⋮ d \\ 3 (5 a + 2 b) - 2 (7 a + 3 b) ⋮ d \end{cases} \Rightarrow \{\begin{cases} 35 a + 15 b - 35 a - 14 b ⋮ d \\ 15 a + 5 b - 14 a - 6 b ⋮ d \end{cases} \Rightarrow \{\begin{cases} b ⋮ d \\ a ⋮ d \end{cases}$