Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 4) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 4)
Lời giải:
- Tìm điểm A’ đối xứng với A qua d
- Nối A’B cắt d tại M. M chính là điểm cần tìm.
- Thật vậy : Vì A’ đối xứng với A qua d cho nên MA = MA’.
Do đó : MA + MB = MA’ + MB = A’B .
- Giả sử tồn tại M’ khác M thuộc d thì : M’A + M’B = M’A’ + M’B lớn hơn hoặc bằng A'B. Dấu bằng chỉ xảy ra khi A’M’B thẳng hàng. Nghĩa là M trùng với M’
Lời giải:
Vì hai điểm A, B phân biệt nên có thể vẽ được đường thẳng d’ đi qua hai điểm đó.
Hai điểm A, B không thuộc d thì d’ không trùng với d
Theo đầu bài, ta cần ba điểm A, B, C thẳng hàng nghĩa là C phải nằm trên đường thẳng d’ mà C phải thuộc vào d. Do đó C là giao điểm của hai đường thẳng d và đường thẳng d’.
+) Nếu d’ và d không có giao điểm nghĩa là d’ song song với d thì không thể tìm được điểm C như vậy.
A. 116 tam giác
B. 80 tam giác
C. 96 tam giác
D. 60 tam giác
Lời giải:
Chọn A
Số tam giác được tạo thành từ 10 điểm là C310 tam giác
Do 4 điểm A1, A2, A3, A4 thẳng hàng nên số tam giác mất đi là C34
Vậy số tam giác thỏa mãn yêu cầu Đề bài: C310−C34=116 là tam giác
Bài 4: Tìm giá trị nhỏ nhất, giá trị lớn nhất
y = 3sin(3x + π6) + 4cos(3x + π6)
Lời giải:
y = 5[35sin(3x + π6) + 45cos(3x + π6)]
y = 5 . sin(3x + π6 + a) với cosa = 35
Do −1≤sin(3x + π6 + a)≤1
⇒-5≤y≤5
Lời giải:
Gọi số sách quyên góp của 3 lớp 7A, 7B, 7C lần lượt là a (quyển), b (quyển), c (quyển)
(điều kiện
Theo đầu bài ta có: và c – a = 22
Áp dụng tính chất:
Ta có:
Ta có:
Vậy số sách quyên góp của lớp 7A, 7B, 7C lần lượt là:
33 (quyển), 44 (quyển), 55 (quyển).
Bài 6: Cho các số hữu tỉ là a, b, c khác 0 thỏa mãn :. Tính giá trị của biểu thức
Lời giải:
Theo bài ra, ta có:
áp dụng tính chất ta có:
thay 1, 2 và 3 vào biểu thức M ta có:
Vậy M = 8
Bài 7: Cho biết và x + y + z =120 .Tìm x,y,z
Lời giải:
Theo tính chất dãy tỉ số bằng nhau ta có:
Vậy
tan2x - sin2x = tan2x . sin2x
Lời giải:
Bài 9: Cho hai điểm A(x1; y1) và B(x2; y2) với . Chứng minh rằng nếu đường thẳng y = ax + b đi qua A và B thì
Lời giải:
Vì đường thẳng đi qua A nên tọa độ điểm A thỏa mãn: y1 = ax1 + b (1).
Đường thẳng đi qua B nên tọa độ điểm B thỏa mãn: y2 = ax2 + b (2)
Trừ vế với vế của (1) cho (2) ta được:
Do đó ta có: .
Bài 10: Cho hàm số y = -x + 5 có đồ thị là (d1)
A) Vẽ (d1), (d2) trên cùng mặt phẳng tọa độ
B) Tìm tọa độ giao điểm của (d1), (d2)
Lời giải:
y = -x + 5
Cho dths đi qua A(0; 5)
cho dths đi qua B(5; 0)
Nối A; B ta được dths y = -x + 5
cho dths đi qua C(0; -1)
cho dths đi qua D(2; 0)
Nối C; D ta được dths cần tìm
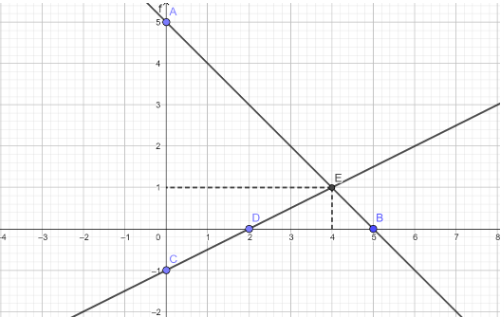
b) Từ dths ta thấy tọa độ giao điểm của 2 hàm số là E(4; 1)
A.
B.
C. m = 2
D. m = −2
Lời giải:
Nhận thấy
Ta thay tọa độ điểm M vào phương trình d1 được phương trình
Vậy
Đáp án cần chọn là: A.
A. 3 cm
B. 6cm
C. 9cm
D. 12cm
Lời giải:
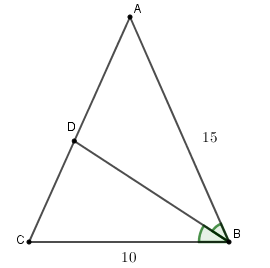
Vì BD là đường phân giác của nên:
Suy ra: (theo tính chất dãy tỉ số bằng nhau) .
Mà tam giác ABC cân tại A nên AC = AB = 15cm
Đáp án: C
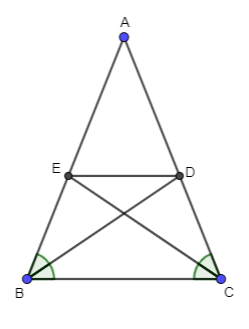
Lời giải:
cân tại A nên (t/c tam giác cân)
Mà
Nên
Xét và có:
(cmt)
BC là cạnh chung
(cmt)
Do đó, (g.c.g)
BE = CD (2 cạnh tương ứng)
Mà AB = AC (gt) nên AB - BE = AC - CD
AE = AD
cân tại A (đpcm)
A. M(1; 3; 0).
B. M(1; −3; 0).
C. M(3; 1; 0).
D. M(2; 6; 0).
Lời giải:
+ Ta tìm điểm I(a; b; c) thỏa mãn
Hay
+ Khi đó:
với H là hình chiếu của I trên (Oxy) và H(1; 3; 0)
Do đó
khi hay M(1;3;0)
Đáp án cần chọn là: A
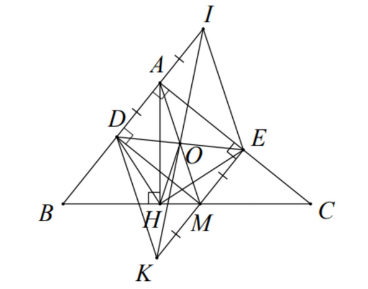
Bài 15: Cho vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D.
a) Chứng minh BE = CD, AD = AE.
b) Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứng minh vuông cân.
c) Từ A và D vẽ các đường thẳng vuông góc với BE. Các đường này cắt BC tại K và H. Chứng minh HK = KC.
Lời giải:
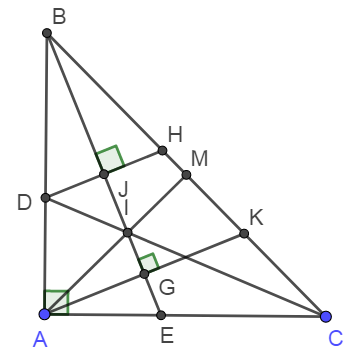
a) Do tam giác ABC vuông cân nên ^ABC =^ ACB⇒^ABE = ^ACD
Xét tam giác vuông ABE và tam giác vuông ACD có:
AB = AC (gt)
^ABE = ^ACD
⇒ΔABE = ΔACD (Cạnh góc vuông - góc nhọn kề)
⇒ BE = CD; AE = AD
b) I là giao điểm của hai tia phân giác góc B và góc C của nên AI cũng là phân giác góc A.
Do ΔABC cân tại A nên AI là phân giác đồng thời là đường cao và trung tuyến.
Vậy thì ^AMC = 90o; BM = MC = AM
Từ đó suy ra ΔAMC vuông cân tại M.
c) Gọi giao điểm của DH, AK với BE lần lượt là J và G.
Do DH và AK cùng vuông góc với BE nên ta có
ΔBDJ = ΔBHJ; ΔBAG = ΔBKG⇒BD = BH; BA = BK
⇒HK=AD
Mà AD = AE nên HK = AE. (1)
Do ΔBAK cân tại B, có o⇒^BAK = 180o - 45o2 = 67,5o
⇒^GAE = 90o - 67,5o = 22,5o = ^IAE2
Suy ra AG là phân giác góc IAE.
Từ đó ta có ^KAC = ^ICA( = 22,5o)
⇒ΔAKC = ΔCIA(g - c - g)⇒KC = IA
Lại có ΔAIE có AG là phân giác đồng thời đường cao nên nó là tam giác cân, hay AI = AE. Suy ra KC = AE (2)
Từ (1) và (2) suy ra HK = KC.
Bài 16: 39100 viết dưới dạng số thập phân là:
A. 3,09
B. 3,900
C. 3,009
D. 3,90
Lời giải:
Chọn A
39100=3,09
Vậy 39100 được viết dưới dạng số thập phân là 3,09
A. 20
B. 15
C. 30
D. 45
Lời giải:
Chọn 3 nam trong 5 nam là số tổ hợp chập 3 của 5 phần tử:
Chọn 2 nữ trong 3 nữ là số tổ hợp chập 2 của 3 phần tử:
Số cách chọn thỏa mãn Đề bài: là
Bài 18: Cho tam giác ABC có AB = AC và tia phân giác góc A cắt BC ở H.
a) Chứng minh
b) Chứng minh AH ⊥ BC
c) Vẽ và . Chứng minh: DE // BC
Lời giải:
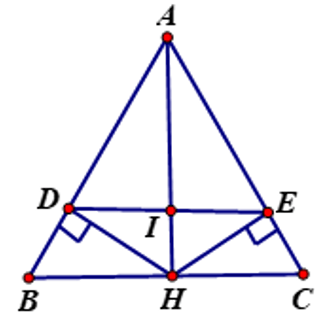


Bài 19: Cho ΔABC có AB = AC. Tia phân giác của góc A cắt BC tại D.
a) Chứng minh tam giác ABD bằng tam giác ADC.
b) Kẻ DH⊥AB (h tập hợp AB ) DK⊥AC ( K ∈ AC) Chứng minh BH = CK.
c) Biết ˆA = 4ˆB tính số đo các góc của tam giác ΔABC
Lời giải:
a)Ta có: AB = AC, ^BAD = ^DAC→ΔABD = ΔACD(c . g . c)
b)Từ câu a ⇒ DB = DC
Mà ^DHB =^ DKC = 90o, ^ABC = ^ACB
⇒ΔDHB = ΔDKC (cạnh huyền – góc nhọn)
⇒BH = CK
c) Ta có : AB = AC suy ra tam giác ABC cân tại A
⇒ˆB=ˆC
Mà ˆA = 4ˆB
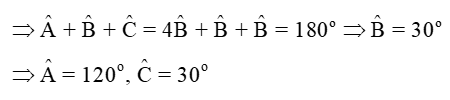
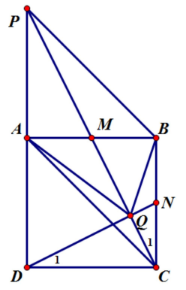
Bài 20: Cho hình vuông ABCD, M là trung điểm cạnh AB, P là giao điểm CM và DA
a) Cm: APBC là hình bình hành và BCDP là hình thang vuông
b) CM: 2Sbcdp = 3Sapbc
c) Gọi N là trung điểm BC, Q là giao điểm DN và CM. Cm: AQ = AB
Lời giải:
a) Ta có: (2 góc đổi đỉnh)
Xét tứ giác APBC có AB và CP là 2 đường chéo nhau tại trung điểm mỗi đường nên APBC là hình bình hành.
Vì APBC là hình bình hành nên mà
BCDP là hình thang vuông (Điều phải chứng minh).
b) Nhận xét: và đặt
Khi đó:
Suy ra đpcm.
c) Vì M là trung điểm của AB nên
Vì N là trung điểm của BC nên mà
mà vuông tại C nên
vuông tại Q.
Xét vuông tại Q, có QA là đường trung tuyến ứng với cạnh huyền
mà (Điều phải chứng minh).
a) Chứng minh rằng: BM = CN
b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN.
c) Đường trung trực của MN và tia phân giác của cắt nhau tại K. Chứng minh rằng từ đó suy ra KC vuông góc với AN
Lời giải:
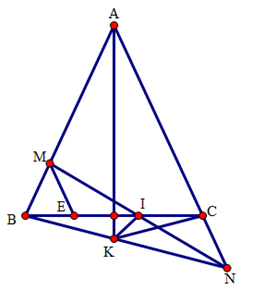
a) Do tam giác ABC cân tại A, suy ra AB = AC.
Ta có: AM + AN = AB – BM + AC + CN = 2AB – BM + CN.
Ta lại có AM + AN = 2AB (gt), nên suy ra
2AB – BM + CN = 2AB ⇔ – BM + CN = 0 ⇔ BM = CN.
Vậy BM = CN (đpcm).
b) Gọi I là giao điểm của MN và BC.
Qua M kẻ đường thẳng song song với AC cắt BC tại E.
Do ME // NC nên ta có:
(hai góc đồng vị) nên ∆BME cân tại M ⇒ BM = ME mà BM = CN nên ME = CN.
(hai góc so le trong)
(hai góc so le trong)
Ta chứng minh được
Suy ra MI = NI (hai cạnh tương ứng), từ đó suy ra I là trung điểm của MN.
c) Xét hai tam giác MIK và NIK có:
MI = IN (cmt),
IK là cạnh chung. Do đó
Suy ra KM = KN (hai cạnh tương ứng).
Xét hai tam giác ABK và ACK có: AB = AC(gt), (do BK là tia phân giác của ), AK là cạnh chung, do đó
Suy ra KB = KC (hai cạnh tương ứng).
Xét hai tam giác BKM và CKN có: MB = CN, BK = KN, MK = KC, do đó
suy ra .
Mà (đpcm)
Bài 22: Tính bằng cách thuận tiện nhất: 34 000 : 125 : 8
Lời giải:
372,95 : 3
757,5 : 35
431,25:125
35,1 x 8,5
Lời giải:
372,95 : 3 = 124.316666667
757,5 : 35 = 21.6428571429
431,25:125 = 3.45
35,1 x 8,5 = 298.35
Bài 24: Phân tích thành nhân tử 5(x + 3y) - 15x (x + 3y)
Lời giải:
5(x + 3y) - 15x ( x + 3y ) = (x + 3y)(5 - 15) = -10(x + 3y)
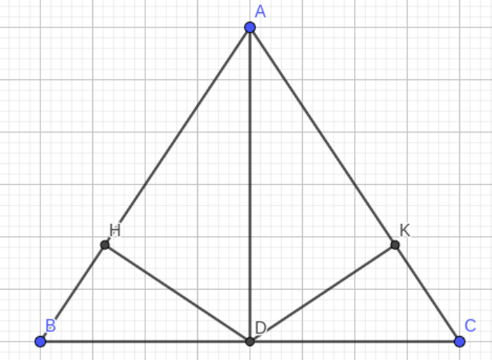
a) Chứng minh A, E, D thẳng hàng và BCED là hình thang.
b) Chứng minh .
c) Cho biết AB = 3cm, AC = 4cm. Tính DE và diện tích DHE.
Lời giải:
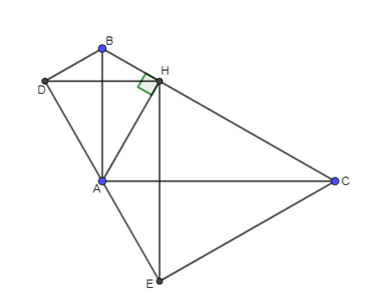
a) Do D đối xứng với H qua đoạn AB nên cân tại A
có AB là đường cao đồng thời là phân giác
Tương tự với
Ta có :
D, A, E thẳng hàng
Nhận thấy
đối xứng với qua đoạn thẳng AC (1)
Tương tự , ta cũng có : (2)
Từ (1) và (2) BD // EC (do 2 góc trong cùng phía bù nhau)
b) Ta có : đồng dạng với
Suy ra tỷ lệ
Mà BH = BD , HC = CE
(Do AD = AH = AE)
.
c) Ta có: AD = AH (tính chất đối xứng), AH = AE (tính chất đối xứng)
Suy ra AD = AE mà A, D, E thẳng hàng nên A là trung điểm của DE.
Xét tam giác vuông ABC, vuông tại A, có:
⇒ DE = cm.
Xét tam giác ABC vuông tại A có:
Xét tam giác DHE vuông tại H, có:
Vậy diện tích tam giác DEH là: (đvdt).
Bài 26: Cho có A(5; 3); B(2; -1) và C(-1; 5). Tính tọa độ chân đường cao vẽ từ A.
A. (1; 2)
B. ( 1; 1)
C. (1; -1)
D. (-2; 1)
Lời giải:
Chọn B.
Gọi A’(x; y) là tọa độ chân đường cao vẽ từ A;
và
Ta có AA’ và BC vuông góc với nhau nên
Suy ra -3(x - 5) + 6(y - 3) = 0 hay x - 2y + 1 = 0 (1)
Và cùng phương nên 2x + y – 3 = 0 (2)
Từ (1) và (2) suy ra x = y = 1
Vậy điểm A’ cần tìm có tọa độ (1; 1).
Bài 27: Cho tam giác ABC có AB = 3; AC = 5; Gọi M là điểm thuộc đoạn BC sao cho BM = 2MC. Tính
Lời giải:
Áp dụng định lý cos, ta có:
Bài 28: Cho có AB = 6cm, AC = 3cm, , M là điểm thỏa mãn . Tính độ dài đoạn AM.
A.
B.
C.
D.
Lời giải:
Áp dụng định lý coscos ta được:

Mặt khác:
Áp dụng định lý Pytago ta được:
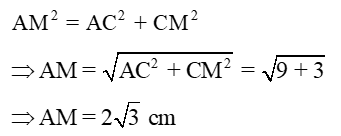
Lời giải:
F là trung điểm AB ; E là trung điểm AC
Ta có EF song song BC (đường trung bình)
Mà D là trung điểm BC I là trung điểm EF AI là trung tuyến
Theo tính chất trọng tâm:
DE là đường trung bình tam giác ABC
hay
D là trung điểm BC
Bài 30: Số lớn nhất có 4 chữ số khác nhau và tích các chữ số bằng 24 là ………
Lời giải:
Tách 24 thành các tích tương ứng gồm các thừa số là số có 1 chữ số:
24 = 6 × 4
24 = 8 × 3
24 = 8 × 3 × 1
24 = 6 × 4 × 1
24 = 4 × 3 × 2 × 1
Số cần tìm là số lớn nhất có 4 chữ số khác nhau nên trong 3 tích vừa tìm được chỉ có tích 4 × 3 × 2 × 1 thỏa mãn yêu cầu Đề bài:
Nên số lớn nhất có 4 chữ số khác nhau và tích các chữ số bằng 24 là 4321
Vậy số cần tìm là 4321
Lời giải:
ĐKXĐ: x > 1 hoặc x < −1
Từ pt x > 0. Kết hợp vs ĐKXĐ, ta có: x > 1
Pt
Đặt
Pt trở thành: (nhận) hoặc (loại)
hay
hoặc (vì x>1x>1)
Lời giải:
Đặt
Xét vế trái
Xét vế phải
Từ (1) và (2) ta có Đpcm
A. Hình thang.
B. Hình bình hành.
C. Hình chữ nhật.
D. Tứ diện vì MN và BD chéo nhau.
Lời giải:
Đáp án đúng là: A
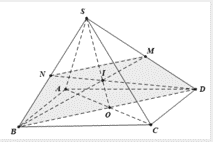
+) Tam giác SBD có SO là đường trung tuyến; điểm I nằm trên đoạn SO; .
nên I là trọng tâm tam giác SBD.
⇒ M là trung điểm SD, N là trung điểm SB.
+) Tam giác SBD có MN là đường trung bình nên MN// BD và
⇒ Nên MNBD là hình thang.
M,N lần lượt là trung điểm các cạnh SA và SD.
1. Chứng minh MO song song với mặt phẳng (SBC) và mặt phẳng OMN) song song với mặt phẳng (SBC).
2. Gọi K là trung điểm của MO. Chứng minh NK song song với (SBC).
3. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (OMN). Hỏi thiết diện là hình gì ?
Lời giải:
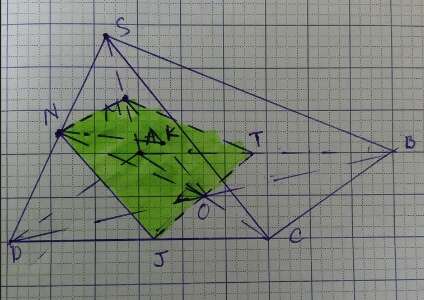
1) Ta có: MO là đường trung bình ΔSAC nên MO//SC mà SC⊂(SBC)
Vậy MO//(SBC)
Ta có:
MO//SC
NO//SB
MO, NO⊂(OMN); SC, SB⊂(SBC)
Vậy (OMN)//(SBC)
2) Ta có: (OMN)//(SBC)
Mà NK ⊂ (OMN)
Nên NK//(SBC)
3) Xét (OMN) và (ABCD):
Ta Có:
+) O là điểm chung 1
+) NM//AD (đường TB của tam giác)
Qua O vẽ đường thẳng song song với AD cắt AB tại T, cắt CD tại J
Vậy JT =(OMN) ∩ (ABCD) (1)
(OMN) ∩ (SAD)=MN (2)
(OMN) ∩ (SCD)=NJ (3)
(OMN) ∩ (SAB)=MT (4)
Từ 4 điều trên vậy thiết diện hình thang NMTJ (vì NM//TJ//AD).
a) Xác định giao tuyến của hai mặt phẳng (SBD) và (SAC).
b) Gọi K là trung điểm của SD. Tìm giao điểm G của BK với mặt phẳng (SAC); hãy cho biết tính chất của điểm G.
Lời giải:
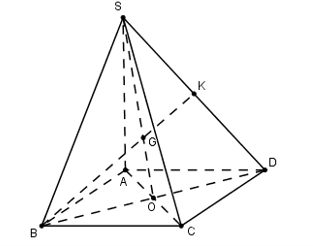
a) Gọi (1)
Mà (2)
Từ (1) và (2)
b) Trong mặt phẳng (SBD) gọi
Ta có mà BK và SO là các đường trung tuyến của tam giác SBD
G là trọng tâm tam giác SBD.
Bài 36: Cho hình thang vuông ABCD có , . Gọi E là trung điểm của CD
a/ Tứ giác ABCE là hình gì?
b/ Tứ giác ABED là hình gì?
c/ Gọi M là giao điểm của AC và BE, K là giao điểm của AE và DM, O là giao điểm hai đuờng chéo hình vuông ABED. Kẻ DH vuông góc với AC cắt AE tại I. Chứng minh DB là tia phân giác của
d/ Chứng minh BIDK là hình thoi
Lời giải:
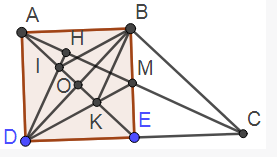
a) Xét tứ giác ABCE có AB song song và bằng EC (gt) nên nó là hình bình hành.
b) Xét tứ giác ABED có AB song song và bằng DE (gt) nên nó là hình bình hành.
Lại có nên ABED là hình chữ nhật.
Lại có AB = AD nên ABED là hình vuông.
c) Xét tam giác AME và DMB có :
ME = B
AE = DB (Hai đường chéo hình vuông)
(ABED là hình vuông)
Xét hai tam giác vuông AHI và DOI có:
(Hai góc đối đỉnh)
(Cùng phụ với hai góc bên trên) (2)
Từ (1) và (2) ta có: hay DO là tia phân giác của góc
d) Xét IDK có DO là tia phân giác đồng thời là đường cao nên nó là tam giác cân tại D.Vậy thì DO là đường trung tuyến hay OI = OK.
Do ABED là hình vuông nên O là trung điểm BD.
Xét tứ giác DIBK có O là trung điểm hai đường chéo nên DIBK là hình bình hành.
Lại có nên DIBK là hình thoi.
Bài 37: Cho ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.
Lời giải:
M, N lần lượt là trung điểm AB, AC nên MN là đường trung bình của ABC ứng với cạnh BC
hay
MNPH là hình thang (∗)
Mặt khác:
Tam giác vuông ABH có HM là đường trung tuyến ứng với cạnh huyền nên
(bổ đề quen thuộc)
MHB cân tại M
Mà (hai góc đồng vị với NP // AB)
Hay
Từ (∗); (∗∗) MNPH là hình thang cân (đpcm)
Bài 38: Cho ABC vuông tại A; đường phân giác BE. Kẻ EH BC (H ∈ BC). Gọi K là giao điểm của AB và HE.
a) ΔABE = ΔHBE.
b) BE là đường trung trực của đoạn thẳng AH.
c) EK = EC.
d) AE < EC.
Lời giải:
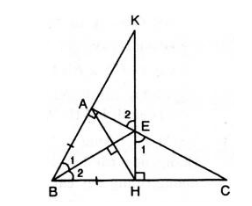
a) Xét ΔABE và ΔHBE ta có :
BE là cạnh chung
Do đó (cạnh huyền – góc nhọn).
b) Vì (chứng minh trên)
Suy ra BA = BH, EA = EH (các cặp cạnh tương ứng)
EB là đường trung trực của AH.
c) Xét và ta có:
AE = EH (chứng minh trên)
(hai góc đối đỉnh).
Do đó (g.c.g).
Suy ra EK = EC (hai cạnh tương ứng).
d) vuông tại H có EH < EC (do cạnh huyền là lớn nhất trong tam giác vuông).
Mà EH = AE (câu b) nên AE < EC.
Bài 39: Cho vuông tại A điểm M thuộc cạnh BC từ M vẽ các đường thẳng vuông góc với AB ở D vuông góc
a) cm AM = BE.
b) gọi l là điểm đx của D qua A và K là điểm đx của E qua M cm IK, DE, AM đồng quy hai trung điểm O của mỗi đoạn.
c) gọi AH là đường cao của tính số đo .
Lời giải:
a) Xét tứ giác ADME có
ADME là hình chữ nhật
AM= DE
b) Gọi O là giao điểm của AM và DE OA = OM = OD = OE (2)
Do ADME là hình chữ nhật DA = ME
2DA = 2ME hay DA + AI = EM + MK (vì DA = AI; ME = MK)
DI = EK
Xét tứ giác DIEK có DI = EK (cmt)
DI // EK (vì CEDM là HCN)
DKEI là hình bình hành
Do O là trung điểm của DE KI đi qua O
DE cắt IK tại O và OD = OE; OK = OI (1)
Từ (1) và (2) DE; AM; IK đồng quy tại trung điểm O của mỗi đường
c) Xét AHM vuông tại H có O là trung điểm của AM, khi đó HO là đường trung tuyến ứng với cạnh huyền AM. Suy ra
Mặt khác, AM = DE.
Xét DHO có đường trung tuyến
DHE vuông tại H
Bài 40: Cho tứ giác ABCD có AC cắt BD tại O, . Gọi E là giao điểm của AD và BC CMR:
a) Các tam giác AOB và DOC đồng dạng.
b) Các tam giác AOD và BOC đồng dạng.
c) EA . ED = EB . EC.
Lời giải:
a) Xét và có:
do đó : đồng dạng với (g-g)
b) theo cm câu a: đồng dạng với
Xét và có:
(2 góc đối đỉnh)
Do đó: đồng dạng với (c-g-c)
c) Xét và có:
chung
( 2 góc tương ứng của đồng dạng với )
Do đó: đồng dạng với (g - g)
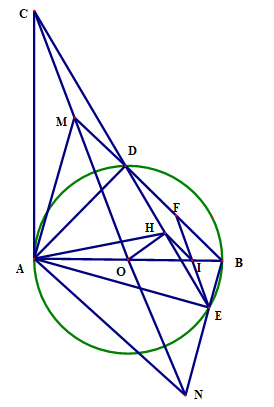
thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.
a) Chứng minh: tứ giác AOHC nội tiếp.
b) Chứng minh: AC . AE = AD . CE
c) Đường thẳng CO cắt tia BD, tia BE lần lượt tại M và N. Chứng minh : AM // BN
Lời giải:
a) Ta có
Vậy tứ giác AOHC nội tiếp.
b) Ta có chung suy ra (g.g)
c) Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F
Vì tứ giác AOHC nội tiếp
Suy ra tứ giác AHIE nội tiếp
Mà H là trung điểm của DE I là trung điểm của EF. Có EF // MN và IE = IF
O là trung điểm của đoạn thẳng MN.
Suy ra tứ giác AMBN là hình bình hành AM//BN.
Lời giải:
Số cách chọn 5 trong 52 quân bài là .
Giả sử 5 quân bài này có 2 quân thuộc bộ A, 2 quân thuộc bộ B, 1 quân thuộc bộ C.
Có 52 cách chọn 1 quân bộ C.
Khi đó chỉ được chọn 4 quân còn lại trong số 12 bộ còn lại (bỏ bộ có quân C đi)
Có cách chọn 2 trong số 12 bộ còn lại.
Mỗi bộ A, B lại có cách chọn.
Vậy có cách chọn.
Vậy xác suất cần tìm là
Bài 43: Cho a, b, c là độ dài 3 cạnh của tam giác. CMR
Lời giải:
Đặt
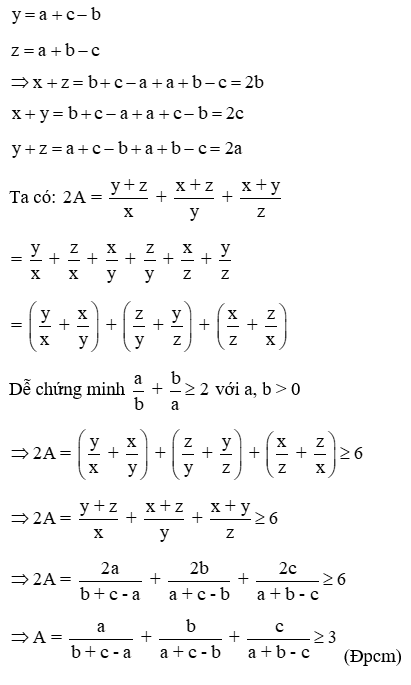
Bài 44: Cho M = 1 x 3 x 5 x 7 x....... x 2023 + 2024. Hỏi M chia cho 5 dư bao nhiêu ?
Lời giải:
Xét có thừa số 5
Có 2024 chia 5 dư 4 (2)
Từ (1) và (2)
M chia cho 5 dư 4
Bài 45: Giải phương trình . Biết số nguyên dương n thỏa mãn
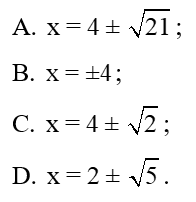
Lời giải:
Đáp án đúng là A
Xét phương trình:
Với n = 4 thì phương trình trở thành: x2 – 8x – 5 = 0
Suy ra phương trình có hai nghiệm .
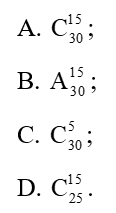
Lời giải:
Trong 30 câu đã chọn 5 câu nên còn lại 25 câu.
Ta cần chọn 15 câu trong 25 câu nên có cách chọn.
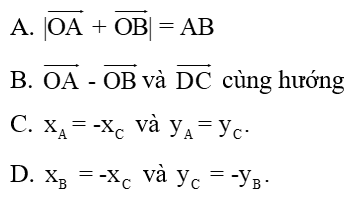
Lời giải:
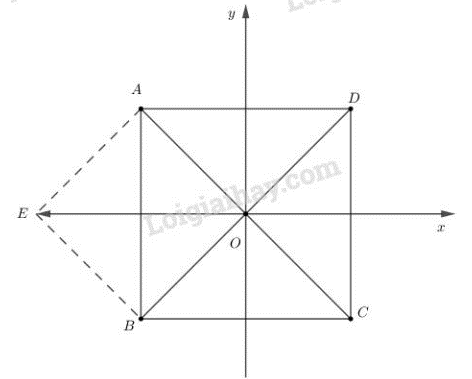
A) Ta có:
A đúng.
B) Vì
Mà và ngược hướng nên B) sai
C) Vì sai.
D) Vì sai.
Chọn A.
Cách giải thích khác:
Qua A kẻ
Ta dễ dàng chứng minh được:
Vậy A) đúng.
Bài 48: Trong hệ tọa độ Oxy, cho ba điểm A(1; 3); B(-1; 2); C(-2; 1). Tìm tọa độ của vectơ
A. (-5; -3)
B. (1; 1)
C. (-1; 2)
D. (-1; 1)
Lời giải:
Đáp án B
Lời giải:
Ta gọi 2 số đó là a và b
Ta có a + b = 10,45 ( 1 )
Theo Đề bài: a + 4b = 22, 45 ( 2)
Lấy (2) - (1) ta có a + 4b - a - b = 22,45 - 10,45 = 12
3b = 12
b = 4
a = 10,45-4 = 6,45
Bài 50: Xác định hàm số bậc 2: y = - 4x + c, biết rằng đồ thị của nó:
a, Đi qua 2 điểm A (1; 2) và B (2;3)
b, Có đỉnh I (-2;-1)
c, Có hoành độ là -3 và đi qua điểm P (-2;1)
d, Có trục đối xứng là đường thẳng x= 2 và cắt trục hoành tại điểm M (3;0)
Lời giải:
a) Do đường thẳng đi qua 2 điểm A(1; 2) và B(2; 3)
Ta có hệ phương trình
b) Do hàm số có đỉnh I(-2; -1)
c) Do hàm số có hoành độ đỉnh bằng -3
Lại có hàm số đi qua P(-2; 1)
Thay x = -2 và y = 1 vào hàm số ta được
d) Do hàm số có trục đối xứng x = 2
Do hàm số cắt trục hoành tại điểm M(3; 0)
Thay x = 3 và y = 0 vào hàm số ta có
9 – 4 . 3 + c = 0
c = 3
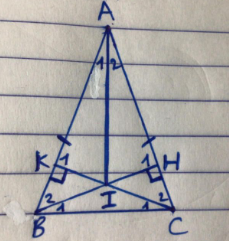
Bài 51: Cho ABC cân tại A ( ). Vẽ BH AC, CK AB.
a) Chứng minh rằng AH = AK.
b) Gọi I là giao điểm của BH và CK. Chứng minh BIC cân.
c) Chứng minh HI là tia phân giác của A
Lời giải:


Bài 52: Cho ABC, lấy điểm M thuộc cạnh AB sao cho . Gọi N là trung điểm của cạnh BC. Tính tỉ số
Lời giải:
N là trung điểm BC
Kẻ đường cao AD và ME ứng với BC
Do AD và ME cùng vuông góc BC
Áp dụng định lý Talet:
Ta có:
Bài 53: Phương trình có 2 nghiệm x1, x2 và có tổng x1 + x2 là:
A. 2
B. 3
C. 4
D. 5
Lời giải:
Đặt khi đó phương trình trở thành
Chọn D
A. 9800
B. 90576
C. 92760
D. 54600
Lời giải:
Trường hợp 1: Chọn 3 nữ, 2 nam ⇒ có cách chọn
Trường hợp 2: Chọn 4 nữ, 1 nam có cách chọn
Do đó có cách chọn.
Chọn B.
Lời giải:
Đáp án đúng là: B
Gọi n là số học sinh nam của lớp (n ∈ ℕ*; n ≤ 28)
⇒ Số học sinh nữ là 30 – n
Ta có: Mỗi lần chọn 3 học sinh từ 30 học sinh cho ta một tổ hợp chập 3 của 30 nên
Gọi N là biến cố:” Chọn được 2 học sinh nam và 1 học sinh nữ”
Việc chọn 2 học sinh nam và 1 học sinh nữ có thể xem 1 công việc 2 công đoạn:
- Công đoạn 1: chọn 2 học sinh nam có
- Công đoạn 2: Chọn 1 học sinh nữ có cách
Mà
Vì nên n = 16
Vậy số học sinh nữ của lớp là : 30 – 16 = 14 (học sinh).
Bài 56: Tổng của 2 vectơ đối bằng bao nhiêu?
Lời giải:
Hai vec tơ đối nhau có tổng bằng không.
Bài 57: Hình thang với hai cạnh bên bằng nhau, góc tù bằng 120o thì có phải là hình thang cân không?
Lời giải:
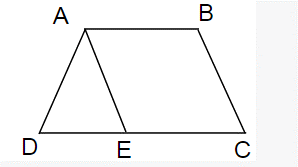
Giả sử: AD = BC; góc DAB = 120o
Vì AB // CD nên góc DAB + ADC = 180o
⇒ góc ADC = 180o - DAB = 180o - 120o = 60o
Trên đoạn CD lấy E sao cho CE = AB
Mà có: CE // AB ⇒ Tứ giác ABCE là hình bình hành ⇒ AE = BC và AE // BC
AE = BC; BC = AD ⇒ AE = AD → tam giác ADE cân tại A ⇒
mặt khác,
Mà góc AED = BCE (do BC // AE) nên
ABCD là hình thang cân.
Bài 58: Hình thang có 2 cạnh bên bằng nhau có phải là hình thang cân không? Vì sao?
Lời giải:
Chưa chắc đã là hình thang cân.
Vì hình thang có 2 cạn bên bằng nhau, có 2 góc bằng nhau, thì mới suy ra là hình thang cân.
Bài 59: Cho hàm số y = x2 và y = mx + 4, với m là tham số.
a) Khi m = 3, tìm tọa độ các giao điểm của hai đồ thị hàm số trên.
A2 (x1 ,y2). Tìm tất cả các giá trị của m sao cho (y1)2 + (y2)2 = 72.
Lời giải:
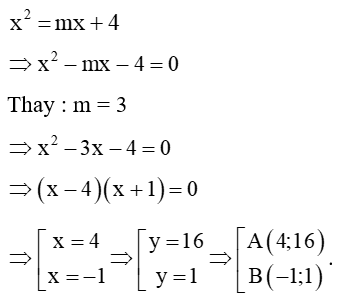
b) Ta có phương trình hoành độ giao điểm:
x2 – mx – 4 = 0.
Ta thấy ∆ = m2 + 16 > 0
Vậy phương trình luôn có hai nghiệm phân biệt x1 và x2.
Áp dụng định lí Vi – et, ta có:
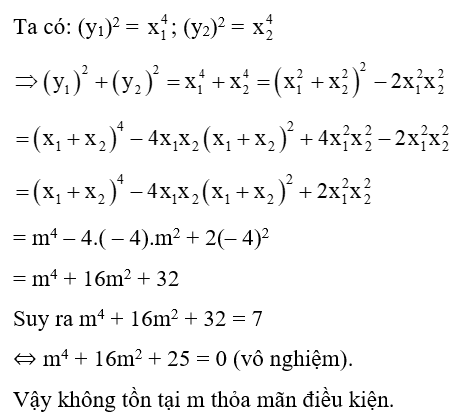
Bài 60: Cho hàm số bậc nhất y = mx - 4. Tìm m trong các trường hợp sau
a) Đồ thị cắt đường thẳng y = 2x - 1 tại điểm hoành độ bằng 2.
b) Đồ thị cắt đường y = -3x + 2 tại điểm có tung độ bằng 5.
Lời giải:
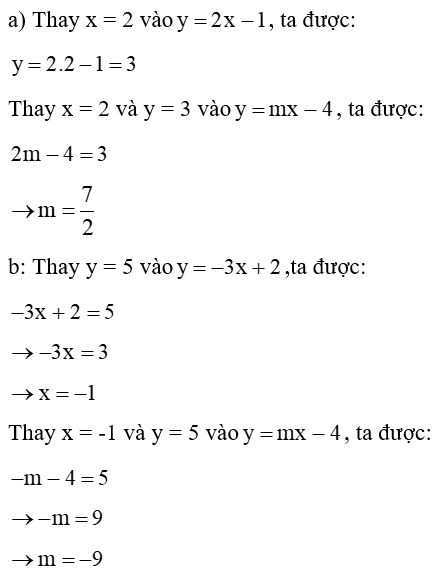
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.