Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 4) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho hình vuông ABCD, M là trung điểm cạnh AB, P là giao điểm CM và DA
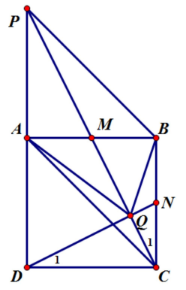
Bài 20: Cho hình vuông ABCD, M là trung điểm cạnh AB, P là giao điểm CM và DA
a) Cm: APBC là hình bình hành và BCDP là hình thang vuông
b) CM: 2Sbcdp = 3Sapbc
c) Gọi N là trung điểm BC, Q là giao điểm DN và CM. Cm: AQ = AB
Lời giải:
a) Ta có: ^M1 = ^M2 (2 góc đổi đỉnh)
⇒ΔAMP = ΔBMC(g . c . g)⇒MP = MC
Xét tứ giác APBC có AB và CP là 2 đường chéo nhau tại trung điểm mỗi đường nên APBC là hình bình hành.
Vì APBC là hình bình hành nên BC // AP⇒BC // DP mà BC ⊥CD
⇒ BCDP là hình thang vuông (Điều phải chứng minh).
b) Nhận xét: SADC = SABC = SABP và đặt SADC = SABC = SABP = a
Khi đó: 2SBCDP = 2 . 3a = 6a; 3SAPBC = 3 . 2a = 6a
Suy ra đpcm.
c) Vì M là trung điểm của AB nên BM = 12AB
Vì N là trung điểm của BC nên CN = 12BC mà
AB = BC⇒BM = CN⇒ΔCBM = ΔDCN(c . g . c)⇒^C1 = ^D1
mà ΔDCN vuông tại C nên
^D1 + ^N1 = 90o⇒^C1 + ^N1 = 90o⇒^CQN = 90o
⇒ΔPDQ vuông tại Q.
Xét vuông tại Q, có QA là đường trung tuyến ứng với cạnh huyền
⇒QA = 12PD = AD mà AD = AB⇒AQ = AB (Điều phải chứng minh).
Bài viết cùng bài học:




