Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 4) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho tam giác ABC vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D.
Bài 15: Cho ΔABC vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D.
a) Chứng minh BE = CD, AD = AE.
b) Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứng minh vuông cân.
c) Từ A và D vẽ các đường thẳng vuông góc với BE. Các đường này cắt BC tại K và H. Chứng minh HK = KC.
Lời giải:
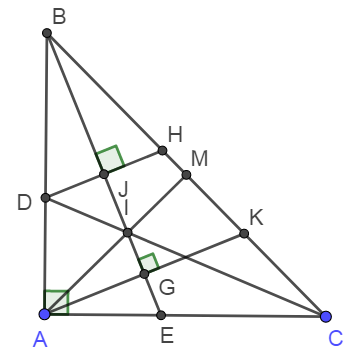
a) Do tam giác ABC vuông cân nên ^ABC =^ ACB⇒^ABE = ^ACD
Xét tam giác vuông ABE và tam giác vuông ACD có:
AB = AC (gt)
^ABE = ^ACD
⇒ΔABE = ΔACD (Cạnh góc vuông - góc nhọn kề)
⇒ BE = CD; AE = AD
b) I là giao điểm của hai tia phân giác góc B và góc C của nên AI cũng là phân giác góc A.
Do ΔABC cân tại A nên AI là phân giác đồng thời là đường cao và trung tuyến.
Vậy thì ^AMC = 90o; BM = MC = AM
Từ đó suy ra ΔAMC vuông cân tại M.
c) Gọi giao điểm của DH, AK với BE lần lượt là J và G.
Do DH và AK cùng vuông góc với BE nên ta có
ΔBDJ = ΔBHJ; ΔBAG = ΔBKG⇒BD = BH; BA = BK
⇒HK=AD
Mà AD = AE nên HK = AE. (1)
Do ΔBAK cân tại B, có o⇒^BAK = 180o - 45o2 = 67,5o
⇒^GAE = 90o - 67,5o = 22,5o = ^IAE2
Suy ra AG là phân giác góc IAE.
Từ đó ta có ^KAC = ^ICA( = 22,5o)
⇒ΔAKC = ΔCIA(g - c - g)⇒KC = IA
Lại có ΔAIE có AG là phân giác đồng thời đường cao nên nó là tam giác cân, hay AI = AE. Suy ra KC = AE (2)
Từ (1) và (2) suy ra HK = KC.
Xem thêm các bài giải Tổng hợp kiến thức môn Toán hay, chi tiết khác:
Bài 4: Tìm giá trị nhỏ nhất, giá trị lớn nhất
Bài 6: Cho các số hữu tỉ là a, b, c khác 0 thỏa mãn :. Tính giá trị của biểu thức
Bài 7: x + y + z =120 .Tìm x,y,z
Bài 9: Cho hai điểm A(x1; y1) và B(x2; y2) với . Chứng minh rằng nếu đường thẳng y = ax + b đi qua A và B thì
Bài 10: Cho hàm số y = -x + 5 có đồ thị là (d1)
Bài 15: Cho vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D.
Bài 16: 39100 viết dưới dạng số thập phân là
Bài 18: Cho tam giác ABC có AB = AC và tia phân giác góc A cắt BC ở H.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.