Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 5) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho hình bình hành ABCD có AB = 2AD. Gọi E, F thứ tự là trung điểm của AB và CD
Bài 20: Cho hình bình hành ABCD có AB = 2AD. Gọi E, F thứ tự là trung điểm của AB và CD
a) Các tứ giác AEFD, AECF là hình gì? Vì sao?
b) Gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật.
Lời giải:
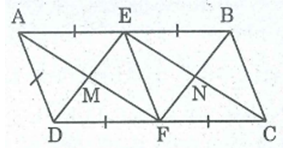
a) Ta có: AE=DE=12AB và AE // DF
→ tứ giác AEFD là hình bình hành
Có thêm AE=AD=12AB
→AEFD là hình thoi (dấu hiệu nhận biết hình thoi)
AE // FC và AE = FC ( vì cùng =12AB )
→ AECF là hình bình hành
b) Tứ giác AECF là hình bình hành nên EN // MF(1)
Chứng minh tương tự câu a tứ giác EBFN là hình bình hành
→ ME // FN(2)
Từ (1) và (2) suy ra EMFN là hình bình hành (3)
Tứ giác AEFD là hình thoi nên suy ra AF⊥DE
→^EMF=90∘ (4)
Từ (3) và (4) suy ra EMFN là hình chữ nhật
Bài viết cùng bài học:




