Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 23) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho đường tròn tâm O bán kính R và một đường thẳng d
Câu 27: Cho đường tròn tâm O bán kính R và một đường thẳng d cố định không giao nhau. Hạ OH vuông góc với d. M là một điểm tùy ý trên d (M không trùng với H). Từ M kẻ hai tiếp tuyến MP và MQ với đường tròn (O; R) (P, Q là các tiếp điểm và tia MQ nằm giữa hai tia MH và MO). Dây cung PQ cắt OH và OM lần lượt tại I và K.
1) Chứng minh rằng tứ giác OMHQ nội tiếp.
2) Chứng minh rằng
3) Chứng minh rằng khi M di chuyển trên đường thẳng d thì điểm I luôn cố định.
4) Biết , tính IP . IQ.
Lời giải:
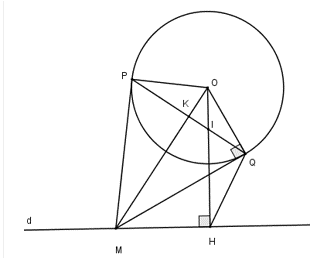
1) Xét tứ giác OMHQ có (MQ là tiếp tuyến của (O))
( )
Vậy tứ giác OMHQ nội tiếp (Tứ giác có hai góc nội tiếp bằng nhau)
2) Ta có: (tổng hai góc nhọn trong tam giác vuông OMH)
Ta có OP = OQ = R, MP = MQ (tính chất hai tiếp tuyến cắt nhau)
→ OM là trung trực của PQ
(tổng hai góc nhọn trong tam giác vuông OIK)
Vậy (cùng phụ với )
3) Xét hai tam giác OIK và OMH có (cmt),
Suy ra (g.g)
Áp dụng hệ thức lượng trong tam giác vuông OQM có
Vì d cố định nên OH không đổi, R luôn không đổi nên OI không đổi. Mà cố định nên I cố định.
4) Xét tứ giác OPMQ có:
Tứ giác OPMQ nội tiếp (Tứ giác có tổng hai góc đối bằng )
(hai góc nội tiếp cùng chắn cung OQ)
Bài viết cùng bài học:




