Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 25) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho nửa đường tròn tâm O có đường kính AB, Ax là tiếp tuyến của nửa đường tròn
Câu 43: Cho nửa đường tròn tâm O có đường kính AB, Ax là tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn nằm cùng phía đối với AB), C là một điểm thuộc nửa đường tròn, H là hình chiếu của C trên AB. Đường thẳng qua O và vuông góc với AC cắt Ax tại M. Gọi I là giao điểm của MB và CH. Chứng minh rằng CI = IH.
Lời giải:
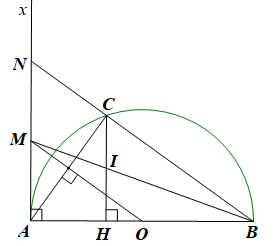
• Gọi N là giao điểm của BC và Ax.
Vì C thuộc đường tròn tâm O đường kính AB nên OA = OB = OC
Do đó DABC vuông tại C nên AC ⊥ BC.
Mà OM ⊥ AC (giả thiết) nên OM // BC hay OM // BN.
Xét DABN có OM // BN và O là trung điểm của AB
Do đó M là trung điểm của AN hay AM = MN.
• Do Ax là tiếp tuyến của (O) nên Ax ⊥ AB
Ta có: CH ⊥ AB, Ax ⊥ AB nên CH // AB.
Xét DABM có IH // AM, theo hệ quả định lí Thalès ta có: .
Xét DMBN có CI // MN, theo hệ quả định lí Thalès ta có: .
Do đó
Mà AM = MN (chứng minh trên) nên IH = CI.
Vậy CI = IH.
Bài viết cùng bài học:
