Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 36) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Tìm số tự nhiên n để giá trị biểu thức sau là số nguyên tố: A = n3 – 4n2 + 4n – 1.
Câu 25: Tìm số tự nhiên n để giá trị biểu thức sau là số nguyên tố: A = n3 – 4n2 + 4n – 1.
Lời giải:
Điều kiện: n ∈ ℕ.
Ta có A = n3 – 4n2 + 4n – 1
= (n3 – 1) – (4n2 – 4n)
= (n – 1)(n2 + n + 1) – 4n(n – 1)
= (n – 1)(n2 + n + 1 – 4n)
= (n – 1)(n2 – 3n + 1).
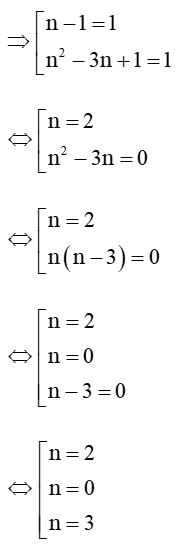
Để A là số nguyên tố thì A là tích của 1 và chính nó (A > 1).
Với n = 2, ta có: A = n3 – 4n2 + 4n – 1 = 23 – 4.22 + 4.2 – 1 = –1 < 1.
Do đó ta loại n = 2.
Với n = 0, ta có: A = n3 – 4n2 + 4n – 1 = 03 – 4.02 + 4.0 – 1 = –1 < 1.
Do đó ta loại n = 0.
Với n = 3, ta có: A = n3 – 4n2 + 4n – 1 = 33 – 4.32 + 4.3 – 1 = 2 > 1.
Do đó ta nhận n = 3.
So với điều kiện n ∈ ℕ, ta nhận n = 3.
Vậy n = 3 thỏa mãn yêu cầu bài toán.
Bài viết cùng bài học:




