Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 66) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho tam giác ABC vuông ở A và hình vuông BCDE. Chứng minh rằng: AB + AC ≤ CE
Câu 13: Cho tam giác ABC vuông ở A và hình vuông BCDE. Chứng minh rằng:
AB + AC ≤ CE.
Lời giải:
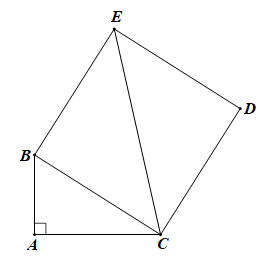
Áp dụng định lí Pythagore cho tam giác vuông ABC ta có: AB2 + AC2 = BC2.
Khi đó (AB + AC)2 = AB2 + AC2 + 2.AB.AC = BC2 + 2.AB.AC
Áp dụng bất đẳng thức Cosi ta có:
2.AB.AC ≤ AB2 + AC2 = BC2
⇒ (AB + AC)2 ≤ BC2 + BC2
Mà BC = BE (do BCDE là hình vuông) và BC2 + BE2 = CE2 (định lí Pythagore cho tam giác vuông BCE)
⇒ (AB + AC)2 ≤ BC2 + BE2 = CE2
⇒ AB + AC ≤ CE
Dấu “=” xảy ra khi AB = AC ⇔ ∆ABC vuông cân ở A.
Xem thêm các bài giải Tổng hợp kiến thức môn Toán hay, chi tiết khác:
Câu 3: Tìm số tự nhiên n để: n2021 + n2020 + 1 là số nguyên tố.
Câu 4: Tìm số nguyên tố p sao cho p + 8 và p + 16 đều là các số nguyên tố.
Câu 9: Chứng minh rằng x5 ‒ x + 2 không là số chính phương với mọi x thuộc ℤ.
Câu 10: Xác định tham số m để hàm số y = f(x) = 3msin4x + cos2x là hàm số chẵn.
Câu 11: 5 phút bằng một phần mấy của giờ?
Câu 13: Cho tam giác ABC vuông ở A và hình vuông BCDE. Chứng minh rằng: AB + AC ≤ CE.
Câu 14: Chứng minh 52n−1.2n+1 + 3n+1.22n−1 chia hết cho 38.
Câu 15: Chứng minh nếu n2 chia hết cho 9 thì n chia hết cho 3 (với n là số tự nhiên).
Câu 16: Tìm số thích hợp để điền vào dãy số sau: 3; 17; 59; 185; 563; …
Bài viết cùng bài học:




