Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 68) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = |f(x) – m + 2018| có 7 điểm cực trị
Câu 9: Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới.
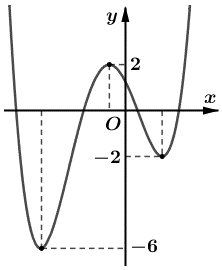
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = |f(x) – m + 2018| có 7 điểm cực trị?
Lời giải:
Quan sát đồ thị, ta thấy hàm số y = f(x) có 3 điểm cực trị.
Do đó để hàm số y = |f(x) – m + 2018| có 7 điểm cực trị thì đồ thị hàm số y = f(x) cắt đường thẳng y = m – 2018 tại 7 – 3 = 4 điểm phân biệt khác 3 điểm cực trị của hàm số y = f(x).
⇔ –2 < m – 2018 < 2.
⇔ 2016 < m < 2020.
Mà m ∈ ℤ.
Suy ra m ∈ {2017; 2018; 2019}.
Vậy có 3 giá trị nguyên dương của m thỏa mãn yêu cầu bài toán.
Xem thêm các bài giải Tổng hợp kiến thức môn Toán hay, chi tiết khác:
Câu 3: Tìm x, y ∈ ℤ, biết: (5x + 1)(y – 1) = 4.
Câu 4: Thực hiện phép tính: C = (x – 2)(x2 + 2x + 4) – x2(x + 2).
Câu 5: Cách xác định cạnh kề, cạnh đối, cạnh huyền trong tam giác vuông.
Câu 7: Cho hàm số y = (m – 1)x + m (1) (với m là tham số, m ≠ 0).
Câu 8: Tìm dư trong phép chia đa thức f(x) = 1 + x2 + x4 + x6 + ... + x100 cho x + 1.
Câu 9: Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới.
Câu 10: Cho tam giác ABC và đường trung tuyến AM. Chứng minh SAMB = SAMC.
Câu 14: Biết đồ thị hàm số y = ax + 5 đi qua điểm M(2; –3) thì hệ số góc bằng bao nhiêu?
Bài viết cùng bài học:




