Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 97) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho tam giác ABC vuông tại A, đường cao AH, vẽ HE vuông góc AB, HF vuông góc AC. Gọi I là trung điểm BC
Câu 74: Cho tam giác ABC vuông tại A, đường cao AH, vẽ HE vuông góc AB, HF vuông góc AC. Gọi I là trung điểm BC.
a) Chứng minh EF = AH.
b) Chứng minh AI vuông góc EF.
c) Gọi M là trung điểm HB, N là trung điểm HC. Chứng minh EMNF là hình thang vuông.
Lời giải:
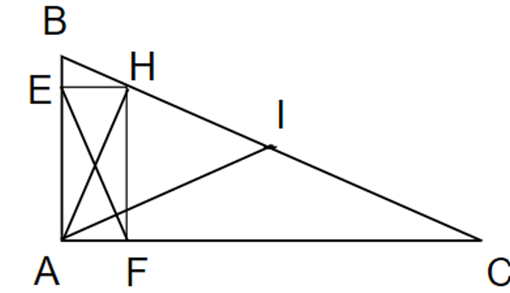
a) Ta có nên EAFH là hình chữ nhật
Suy ra EF = AH (hai đường chéo của một hình chữ nhật)
b) Tam giác ABC vuông tại A có trung tuyến AI
Suy ra AI = = BI = IC
⇒ΔIAB cân tại I nên (1)
EAFH là hình chữ nhật suy ra EF = AH
Gọi O là giao điểm EF và AH
Suy ra EO = OF = OA = OH hay tam giác EOA cân tại O
Nên (2)
Mà
Từ (1), (2) và (3) suy ra hay AI ⊥ EF
c) Xét tam giác EBH vuông tại E có EM là trung tuyến ứng với cạnh huyền
⇒ EM = MB =
⇒ ΔEMB cân tại M
⇒
Mà (do tam giác ABC vuông tại A)
(= )
⇒
⇒
Suy ra: ME vuông góc với EF tại E
Chứng minh tương tự: NF vuông góc với EF tại F
Xét tứ giác MEFN có ME ⊥ EF; NF ⊥ EF
Suy ra: ME // NF
⇒ MENF là hình thang
Đồng thời
⇒ MEFN là hình thang vuông tại E và F.
Bài viết cùng bài học:
