Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 3) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Có thể chia một khối lập phương thành bao nhiêu khối tứ diện có thể tích bằng nhau
Bài 30: Có thể chia một khối lập phương thành bao nhiêu khối tứ diện có thể tích bằng nhau mà các đỉnh của tứ diện cũng là đỉnh của hình lập phương?
Lời giải: Ta chia hình lập phương thành 6 khối tứ diện bằng nhau như sau:
+ Chia khối lập phương thành hai khối lăng trụ tam giác bằng nhau: ABC.A'B'C' và BCD.B'C'D'
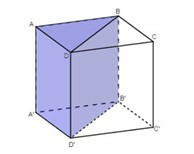
+ Tiếp theo, lần lượt chia khối lăng trụ và thành ba tứ diện: và
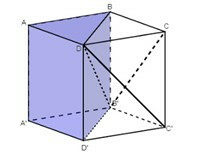
+ Ta chứng minh được các khối tứ diện này bằng nhau như sau:
Hai khối tứ diện DABB' và DAA'B' bằng nhau vì chúng đối xứng nhau qua mặt phẳng (DAB') (1)
Hai khối tứ diện DAA'B' và DD'A'B' bằng nhau vì chúng đối xứng nhau qua mặt phẳng (B'A'D) (2)
Từ (1) và (2) suy ra ba khối tứ diện và bằng nhau.
Tương tự, ba khối tứ diện cũng bằng nhau.
Vậy khối lập phương được chia thành sáu khối tứ diện bằng nhau.
Bài viết cùng bài học:
