Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 69) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có sin^2α + cos^2α = 1
Câu 18: Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có sin2α + cos2α = 1.
Lời giải:
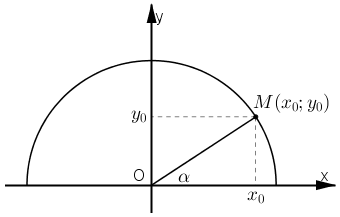
Vẽ đường tròn lượng giác (O; 1).
Với mọi α (0° ≤ α ≤ 180°), ta đều có điểm M(x0; y0) thuộc nửa đường tròn sao cho .
Khi đó ta có: sinα = y0 và cosα = x0.
Mà M thuộc đường tròn lượng giác nên .
⇔ sin2α + cos2α = 1.
Vậy ta có điều phải chứng minh.
Bài viết cùng bài học:
