Cho khối lăng trụ tam giác đều ABC.A'B'C'. Các mặt phẳng (ABC') và (A'B'C') chia khối lăng trụ đã cho thành 4 khối đa diện

Ngọc Nguyễn Ngày: 14-03-2023 Tổng hợp kiến thức

245

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 3) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Cho khối lăng trụ tam giác đều ABC.A'B'C'. Các mặt phẳng (ABC') và (A'B'C') chia khối lăng trụ đã cho thành 4 khối đa diện

Bài 26: Cho khối lăng trụ tam giác đều ABC.A'B'C'. Các mặt phẳng (ABC') và (A'B'C') chia khối lăng trụ đã cho thành 4 khối đa diện. Kí hiệu $H_{1}, H_{2}$ lần lượt là khối có thể tích lớn nhất và nhỏ nhất trong bốn khối trên. Tính giá trị của $\frac{V_{(H_{1})}}{V_{(H_{2})}} .$

Lời giải:

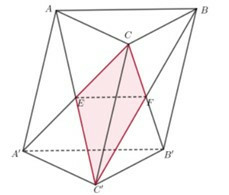
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 3) (ảnh 11)

Gọi $E = A C^{'} \cap A^{'} C$ và $F = B C^{'} \cap B^{'} C .$ Khi đó (ABC') và (A'B'C') chia khối lăng trụ đều ABC.A'B'C' thành 4 khối đa

diện: $C E F C^{'}; F E A^{'} B^{'} C^{'}; F E A B C$ và $F E A B B^{'} A^{'} .$

Gọi V là thể tích của khối lăng trụ đều ABC.A'B'C'. Ta có:

$V_{C . A^{'} B^{'} C^{'}} = V_{C^{''} . A B C} = \frac{1}{3} V; V_{F E A^{'} B^{'} C^{'}} = V_{C . A^{'} B^{'} C^{'}} - V_{C E F C^{'}}; V_{F E A B C} = V_{C . A B C} - V_{C E F C^{'}} \Rightarrow V_{F E A^{'} B^{'} C^{'}} = V_{F E A B C} .$

Mặt khác: $\frac{V_{C E F C^{'}}}{V_{C . A^{'} B^{'} C^{'}}} = \frac{C E}{C A^{'}} \cdot \frac{C F}{C B^{'}} = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} \Rightarrow V_{C E F C^{'}} = \frac{1}{4} V_{C . A^{'} B^{'} C^{'}} = \frac{1}{4} \cdot \frac{1}{3} V = \frac{1}{12} V$

Suy ra

$V_{F E A^{'} B^{'} C^{'}} = V_{F E A B C} = V_{C . A^{'} B^{'} C^{'}} - V_{C E F C^{'}} = \frac{1}{3} V - \frac{1}{12} V = \frac{1}{4} V \Rightarrow V_{F E A B B^{'} A^{'}} = V - 2. \frac{1}{4} V - \frac{1}{12} V = \frac{5}{12} V .$