Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 6) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho đường tròn (O; R), đường kính AB, dây cung DE. Tia DE cắt AB ở C
Bài 47: Cho đường tròn (O; R), đường kính AB, dây cung DE. Tia DE cắt AB ở C. Biết = 90° và OC = 3R.
a) Tính độ dài CD và CE theo R;
b) Chứng minh CD . CE = CA . CB.
Lời giải:
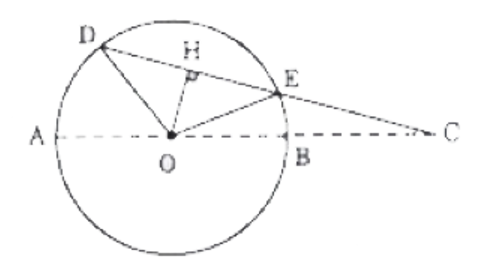
a) Tam giác DOE vuông tại đỉnh O có OD = OE = R, do đó .
Từ O, hạ OH vuông góc với DE tại H, ta tính được .
Tam giác vuông HOC có OC2 = OH2 + HC2 (định lí Pythagore)
Suy ra HC2 = OC2 – OH2 = (3R)2 – = , do đó .
Suy ra CE = HC – HE = .
và CD = HC + HD = .
b) Ta có: CD . CE = .
Lại có: CB = OC – OB = 3R – R = 2R và CA = OC + OA = 3R + R = 4R.
Do đó, CA . CB = 4R . 2R = 8R2.
Vậy CD . CE = CA . CB = 8R2.
Bài viết cùng bài học:




