Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 6) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho hàm số y = (2 – m)x + m + 1 (với m là tham số và m ≠ 2) có đồ thị là đường thẳng d.
Bài 48: Cho hàm số y = (2 – m)x + m + 1 (với m là tham số và m ≠ 2) có đồ thị là đường thẳng d.
a) Khi m = 0, hãy vẽ d trên hệ trục tọa độ Oxy.
b) Tìm m để d cắt đường thẳng y = 2x – 5 tại điểm có hoành độ bằng 2.
c) Tìm m để d cùng với các trục tọa độ Ox, Oy tạo thành một tam giác có diện tích bằng 2.
Lời giải:
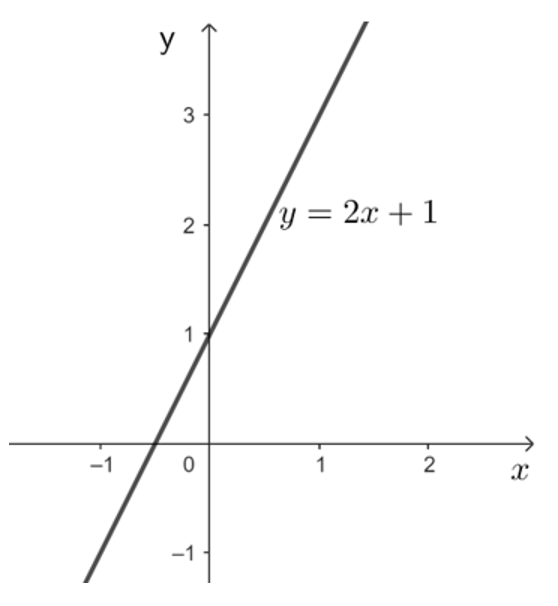
a) Khi m = 0, ta có hàm số: y = 2x + 1.
Với x = 0 thì y = 1, với x = 1 thì y = 3. Do đó đường thẳng d đi qua hai điểm có tọa độ (0; 1) và (1; 3).
b) Ta có d: y = (2 – m)x + m + 1.
Đường thẳng d cắt đường thẳng y = 2x – 5 tại điểm có hoành độ bằng 2, suy ra x = 2.
Suy ra y = 2 . 2 – 5 = – 1.
Do đó, đường thẳng d đi qua điểm có tọa độ (2; – 1). Thay x = 2, y = – 1 vào d ta được:
– 1 = (2 – m) . 2 + m + 1 ⇔ 4 – 2m + m + 1 = – 1 ⇔ m = 6.
c) Ta có d: y = (2 – m)x + m + 1.
+ Cho y = 0, suy ra (do m ≠ 2).
Đường thẳng d cắt trục Ox tại A. Ta có: OA = .
+ Cho x = 0, suy ra y = m + 1.
Đường thẳng d cắt trục Oy tại điểm B(0; m + 1). Ta có: OB = |m + 1|.
SOAB = 2
TH1: m > 2, ta có: (m + 1)2 = 4(m – 2)
⇔ m2 + 2m + 1 = 4m – 8
⇔ m2 – 2m + 9 = 0
.
TH2: m < 2, ta có: (m + 1)2 = – 4(m – 2)
⇔ m2 + 2m + 1 = – 4m + 8
⇔ m2 + 6m – 7 = 0
.
Vậy thì thỏa mãn yêu cầu bài toán.
Bài viết cùng bài học:




