Cho tam giác ABC vuông góc tại A có AC = 12 cm, BC = 16 cm

Ngọc Nguyễn Ngày: 04-04-2023 Tổng hợp kiến thức

344

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 6) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Cho tam giác ABC vuông góc tại A có AC = 12 cm, BC = 16 cm

Bài 54: Cho tam giác ABC vuông góc tại A có AC = 12 cm, BC = 16 cm. Lấy H thuộc BC sao cho CH = 9 cm. Kẻ phân giác của góc ACH cắt AH tại M. Kẻ phân giác của góc BAH cắt BH tại N.

a) Chứng minh: tam giác CAB đồng dạng với tam giác CHA và AH vuông góc BC.

b) Tính NB, NH.

c) Chứng minh MN // AB.

d) MB cắt AN tại O, cắt đường thẳng qua N và song song với AH tại I. Chứng minh $\frac{1}{M O} = \frac{1}{M I} + \frac{1}{M B}$ .

Lời giải:

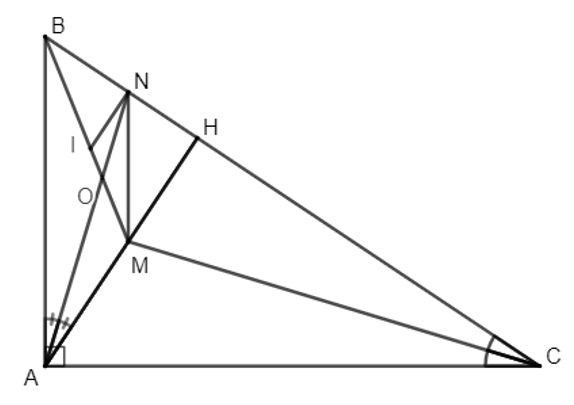
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 6) (ảnh 18)

a) Ta có: $\frac{C A}{C H} = \frac{12}{9} = \frac{4}{3}$ và $\frac{C B}{C A} = \frac{16}{12} = \frac{4}{3}$ . Do đó, $\frac{C A}{C H} = \frac{C B}{C A}$ hay $\frac{C A}{C B} = \frac{C H}{C A}$ .

Xét tam giác ACB và tam giác HCA có:

$\hat{A C B}$ : góc chung

$\frac{C A}{C B} = \frac{C H}{C A}$ (cmt)

Do đó, hai tam giác ACB và HCA đồng dạng (c – g – c).

Suy ra $\hat{A H C} = \hat{B A C} = 90^{\circ}$ nên AH vuông góc với BC tại H.

b) Tam giác ABC vuông tại A, theo định lí Pythagore ta có:

BC² = AB² + AC², suy ra AB² = BC² – AC² = 16² – 12² = 112, suy ra AB = $4 \sqrt{7}$ (cm).

Tam giác AHC vuông tại H, theo định lí Pythagore ta có:

AC² = AH² + HC², suy ra AH² = AC² – CH² = 12² – 9² = 63 ⇒ AH = $3 \sqrt{7}$ (cm).

Ta có: BH + HC = BC, suy ra BH = BC – HC = 16 – 9 = 7 (cm).

Vì AN là tia phân giác của góc BAH nên $\frac{N B}{N H} = \frac{A B}{A H} = \frac{4 \sqrt{7}}{3 \sqrt{7}} = \frac{4}{3}$ .

$\Rightarrow \frac{N B}{N B + N H} = \frac{4}{4 + 3} \Rightarrow \frac{N B}{B H} = \frac{4}{7} \Rightarrow N B = \frac{4}{7} B H = \frac{4}{7} .7 = 4$ (cm).

Suy ra NH = BH – NB = 7 – 4 = 3 (cm).

c) Vì CM là tia phân giác của góc ACH nên $\frac{M H}{M A} = \frac{C H}{A C} = \frac{9}{12} = \frac{3}{4}$ .

Suy ra $\frac{M H}{H A} = \frac{3}{7}$ .

Ta có: $\frac{N H}{H B} = \frac{3}{7}$ . Do đó, $\frac{M H}{H A} = \frac{N H}{H B}$ .

Theo định lí Talet trong tam giác HAB, ta suy ra MN // AB.

Theo giả thiết ta có: NI // AH nên $\frac{M O}{O I} = \frac{A O}{O N} \Rightarrow \frac{M O}{M O + O I} = \frac{A O}{A O + O N} \Rightarrow \frac{M O}{M I} = \frac{A O}{A N}$ .

Theo câu c ta có: MN // AB nên $\frac{M O}{B O} = \frac{N O}{A O} \Rightarrow \frac{M O}{M O + B O} = \frac{N O}{N O + A O} \Rightarrow \frac{M O}{M B} = \frac{N O}{A N}$ .

Từ đó suy ra: $\frac{M O}{M I} + \frac{M O}{M B} = \frac{A O}{A N} + \frac{N O}{A N} = \frac{A O + N O}{A N} = \frac{A N}{A N} = 1$ .

Suy ra $\frac{M O}{M I} + \frac{M O}{M B} = 1 \Leftrightarrow M O (\frac{1}{M I} + \frac{1}{M B}) = 1 \Leftrightarrow \frac{1}{M I} + \frac{1}{M B} = \frac{1}{M O}$ .