Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 21) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d1): y = –x + 2
Câu 35: Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d1): y = –x + 2 và (d2): .
1) Vẽ (d1) và (d2) trên cùng hệ trục tọa độ Oxy.
2) Lấy điểm B trên (d2) có hoành độ bằng –4. Viết phương trình đường thẳng (d3) song song với (d1) và qua điểm B.
3) Tìm tọa độ giao điểm của (d1) và (d2) bằng phép tính.
Lời giải:
1) Bảng giá trị của (d1):
|
x |
0 |
1 |
2 |
|
y |
2 |
1 |
0 |
Bảng giá trị của (d2):
|
x |
–4 |
0 |
4 |
|
y |
–1 |
0 |
1 |
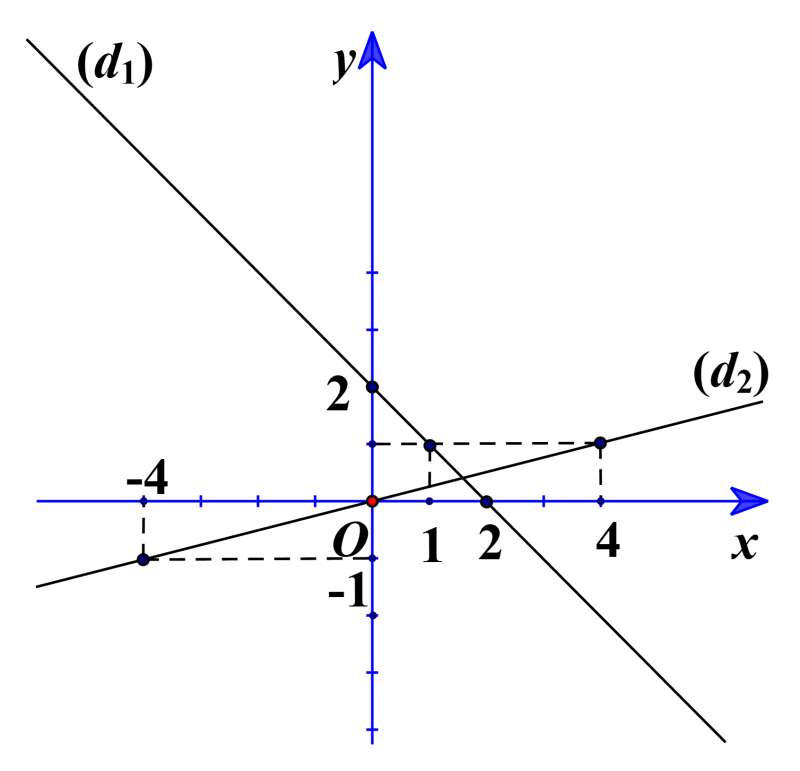
2) Gọi B(–4; yB).
Ta có B(–4; yB) ∈ (d2).
Suy ra .
Do đó tọa độ B(–4; –1).
Vì (d3) // (d1) nên phương trình (d3) có dạng: y = –x + m (m ≠ 2).
Ta có B(–4; –1) ∈ (d3).
Suy ra –1 = 4 + m.
Do đó m = –5 (nhận)
Vậy phương trình (d3): y = –x – 5.
3) Phương trình hoành độ giao điểm của (d1) và (d2): .
.
Với , ta có: .
Vậy giao điểm của (d1) và (d2) là điểm .
Bài viết cùng bài học:




