Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 21) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho x, y, z là các số thực dương thỏa mãn x + y + z = xyz
Câu 23: Cho x, y, z là các số thực dương thỏa mãn x + y + z = xyz. Chứng minh
Lời giải:
Áp dụng bất đăng thức Cauchy, ta có
⇒ 2(xy + yz + zx) ≤ 2(x2 + y2 + z2)
⇔ xy + yz + zx ≤ x2 + y2 + z2
⇔ 3(xy + yz + zx) ≤ x2 + y2 + z2 + 2(xy + yz + zx)
⇔ 3(xy + yz + zx) ≤ (x + y + z)2
.
Áp dụng bất đẳng thức Cauchy, ta có
Ta có
.
Chứng minh tương tự, ta có và .
Khi đó
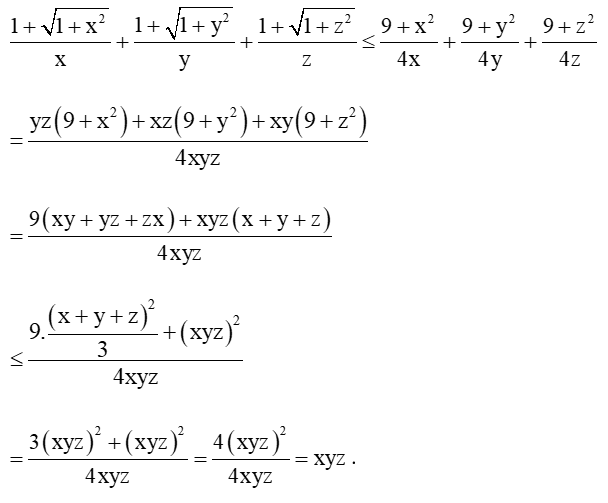
Dấu “=” xảy ra .
Vậy ta có điều phải chứng minh.
Bài viết cùng bài học:




