Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 29) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo
Câu 29: Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo. Vẽ đường thẳng qua B và song song với AC, vẽ đường thẳng qua C và song song với BD, hai đường thẳng đó cắt nhau tại K.
a) Tứ giác OBKC là hình gì ? Vì sao ?
b) Chứng minh rằng AB = OK.
c) Tìm điều kiện của hình thoi ABCD để OBKC là hình vuông.
Lời giải:
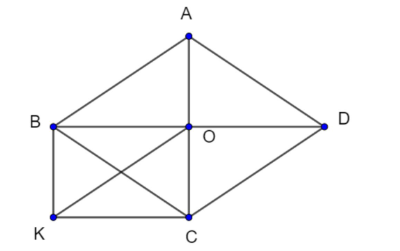
a)
Ta có tứ giác ABCD là hình thoi
Do đó, AC vuông góc với BD (tính chất 2 đường chéo trong hình thoi)
Ta có: BK song song với OC, KC song song với OB
Do đó, Tứ giác BOCK là hình bình hành
Mà
Do đó, BOCK là hình chữ nhật
b)
ABCD là hình thoi nên AB = BC = CD = DA (3)
Do OBIC là hình chữ nhật nên 2 đường chéo OI = BC (4)
Từ (3) và (4) suy ra AB = OI
c)
Để OBKC là hình vuông thì OB = OC
Do đó, ABCD phải là hình vuông.
Bài viết cùng bài học:




