Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 34) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo
Câu 28: Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo. Gọi M, N là trung điểm của OB, OD.
a) Chứng minh AMCN là hình bình hành.
b) AM cắt BC tại E, CN cắt AD tại F. Chứng minh AE = CF và O, E, F thẳng hàng.
Lời giải:
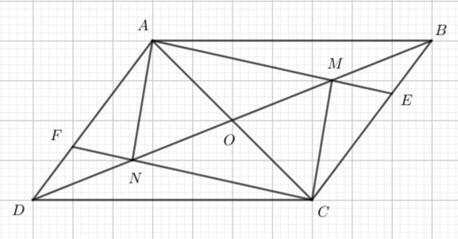
a) Vì O là giao điểm 2 đường chéo của hình bình hành ABCD nên OB = OD.
Mà M, N lần lượt là trung điểm OB, OD nên OM = ON
Mà O là giao điểm 2 đường chéo của hình bình hành ABCD nên OA = OC
Do đó AMCN là hình bình hành (do O là trung điểm AC và MN).
b) Vì AMCN là hình bình hành nên AM // CN hay AE // CF
Mà ABCD là hình bình hành nên AD // BC hay AF // CE
Do đó AECF là hình bình hành nên AE = CF.
Do AECF là hình bình hành mà O là trung điểm của đường chéo AC nên O cũng là trung điểm của đường chéo EF.
Vậy O; E; F thẳng hàng.
Bài viết cùng bài học:




