Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 35) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho tam giác ABC cân tại A, đường cao AD, trực tâm H.
Câu 28: Cho tam giác ABC cân tại A, đường cao AD, trực tâm H. Tính độ dài AD biết AH = 14 cm, BH = HC = 30 cm.
Lời giải:
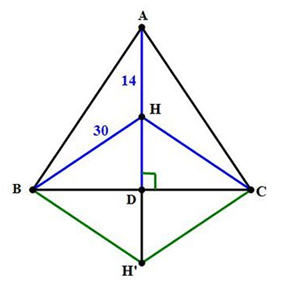
Gọi H’ là điểm đối xứng H qua BC.
Suy ra D là trung điểm của HH’
Vì tam giác ABC cân tại A, AD là đường cao nên AD là trung tuyến
Suy ra D là trung điểm của BC
Xét tứ giác BHCH’ có
D là trung điểm của HH’ và BC;
BC và HH’ là hai đường chéo
Suy ra BHCH’ là hình bình hành.
Mà BH = CH nên hình bình hành BHCH’ là hình thoi
Do đó BH’ // CH, BH = BH’.
Lại có CH ⊥ AB (vì H là trực tâm của tam giác ABC) nên BH’⊥ AB
Hay tam giác ABH’ vuông tại B
Mà BD ⊥ AH’
Suy ra H’B2 = H’D . H’A
⇔ HB2 = HD . (2HD + HA)
⇔ 302 = HD . (2HD + 14)
⇔ 2HD2 + 14HD – 900 = 0
⇔ (HD + 25)(HD – 18) = 0
⇔ HD – 18 = 0 (vì HD > 0)
⇔ HD = 18
Ta có AD = AH + HD = 14 + 18 = 32 cm
Vậy AD = 32 cm.
Bài viết cùng bài học:




