Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 16) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By
Câu 11: Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C và D. Chứng minh rằng đường tròn có đường kính CD tiếp xúc với AB.
Lời giải:
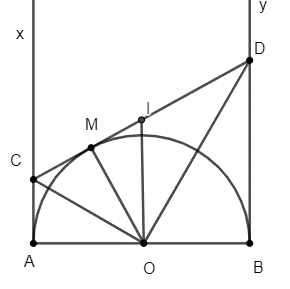
Theo tính chất tiếp tuyến, ta có: Ax ⊥ AB; By ⊥ AB.
Suy ra: Ax // By hay AC // BD.
Suy ra tứ giác ABDC là hình thang.
Gọi I là trung điểm của CD.
Khi đó OI là đường trung bình của hình thang ABDC.
Suy ra: OI // AC ⇒ OI ⊥ AB.
Vì OC và OD lần lượt là phân giác của và nên:
OC OD (tính chất của hai góc kề bù)
Suy ra: IC = ID = IO (tính chất tam giác vuông).
Suy ra I là tâm đường tròn đường kính CD.
Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.
Xem thêm các bài giải Tổng hợp kiến thức môn Toán hay, chi tiết khác:
Câu 1: Chứng minh hằng đẳng thức
Câu 2: Chứng minh: a3 + b3 + c3 = 3abc biết a + b + c = 0.
Câu 7: Cho tam giác ABC có , AB = 3 cm, AC = 6 cm. Tính độ dài đường phân giác AD.
Câu 14: Cho tam giác ABC, chứng minh:
Câu 15: Giải phương trình: sinx + cosx = 1.
Câu 18: Phương trình có bao nhiêu nghiệm thuộc khoảng (−2017π; 2017π)?
Câu 19: Cho A = 75 + 1205 + 2008 + x, (x ∈ ℕ). Tìm điều kiện của x
Câu 20: Viết tập hợp A là các số thỏa mãn 124 < x < 145 bằng cách liệt kê các phần tử.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.