Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 11) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho tam giác ABC. Chứng minh điều kiện cần và đủ để hai trung tuyến BM và CN
Câu 11: Cho tam giác ABC. Chứng minh điều kiện cần và đủ để hai trung tuyến BM và CN vuông góc với nhau là b2 + c2 = 5a2.
Lời giải:
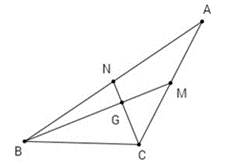
Gọi G là giao điểm của hai trung tuyến BM, CN.
Áp dụng công thức tính trung tuyến, ta có:
• ;
• .
BM và CN vuông góc với nhau khi BG2 + CG2 = BC2.
4a2 + b2 + c2 = 9a2
b2 + c2 = 5a2.
Xem thêm các bài giải Tổng hợp kiến thức môn Toán hay, chi tiết khác:
Câu 1: Tìm x để (x + 17) chia hết cho (x + 3).
Câu 2: Tìm tập hợp X sao cho {a; b} ⊂ X ⊂ {a; b; c; d}.
Câu 3: Tìm tập hợp X sao cho X ⊂ A và X ⊂ B, trong đó
Câu 9: Chứng minh S = 2R2.sin A.sin B.sin C với S là diện tích tam giác ABC.
Câu 12: Cho tam giác ABC. Chứng minh c.mc = b.mb khi b2 + c2 = 2a2.
Bài viết cùng bài học:
